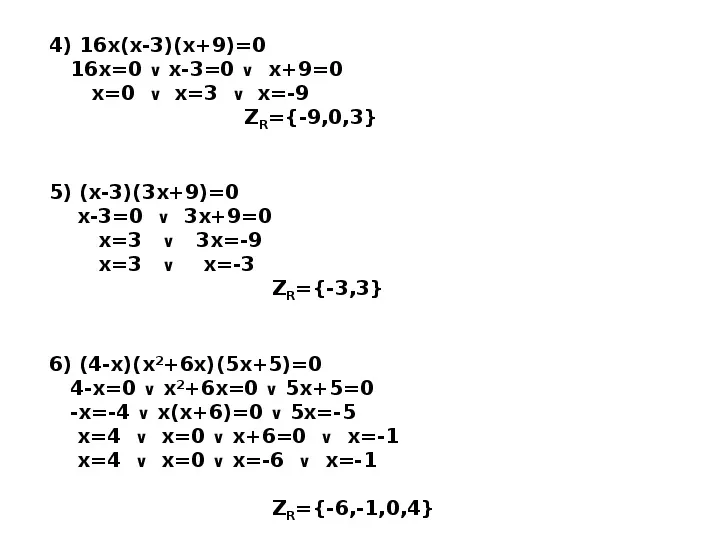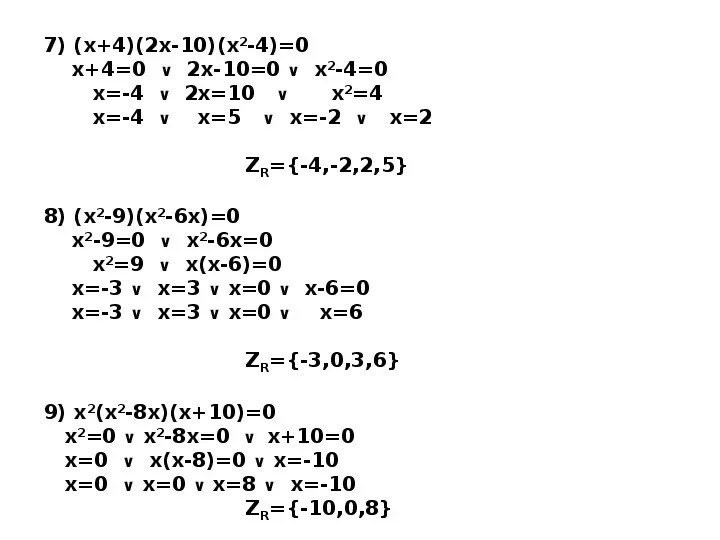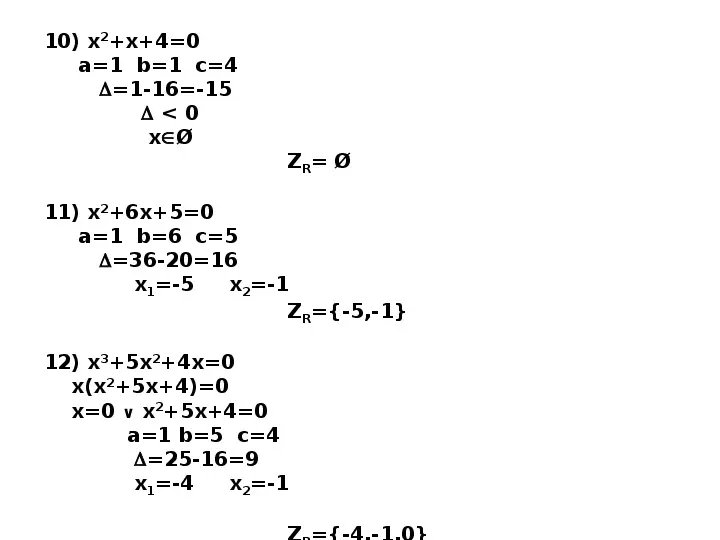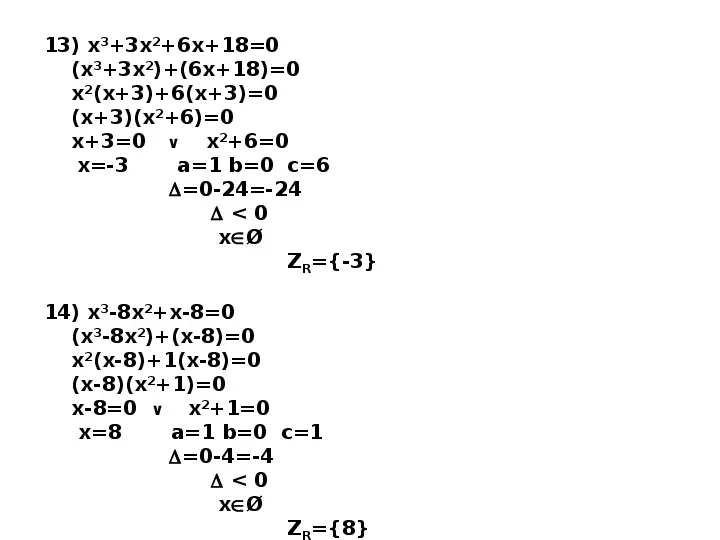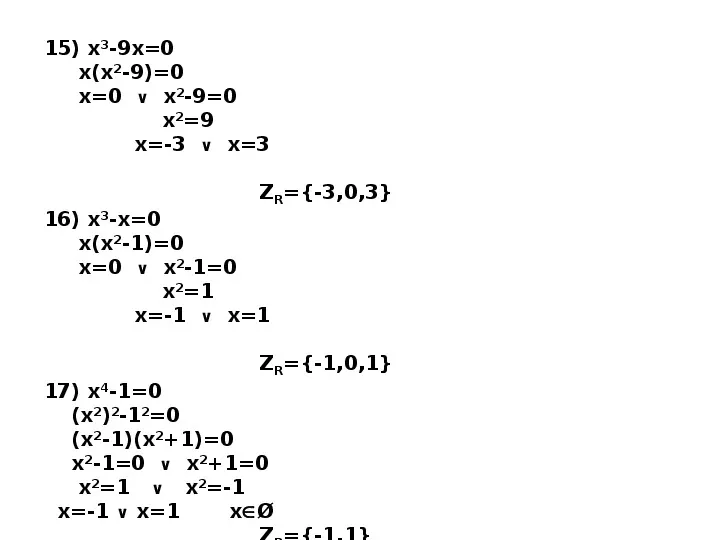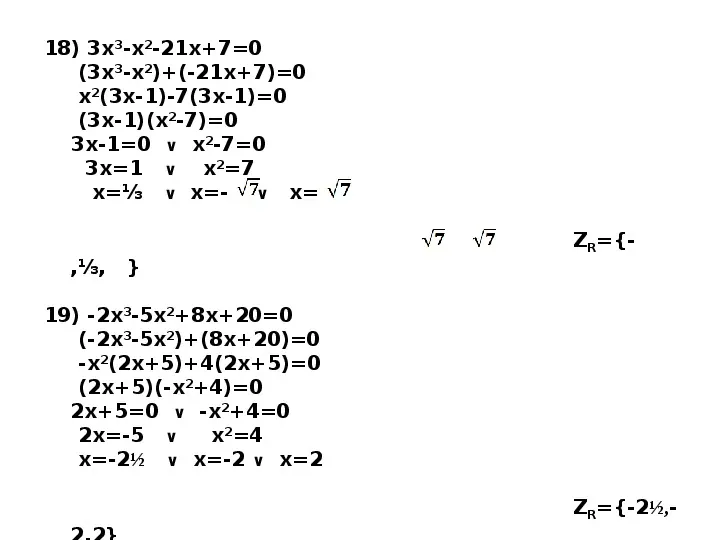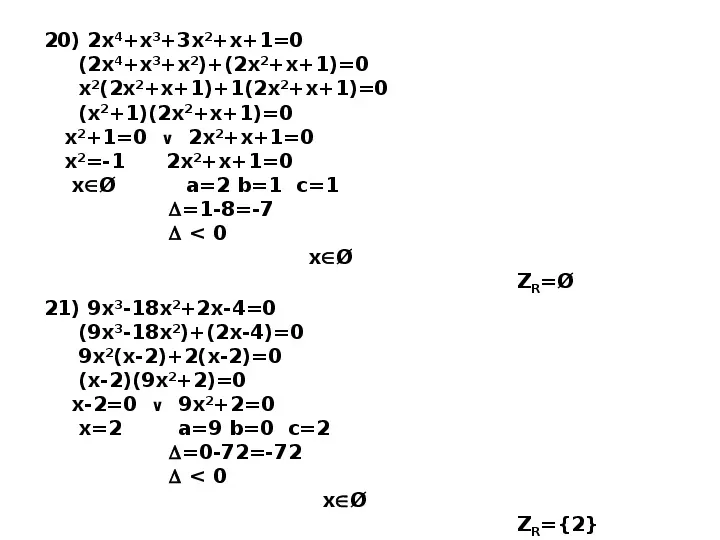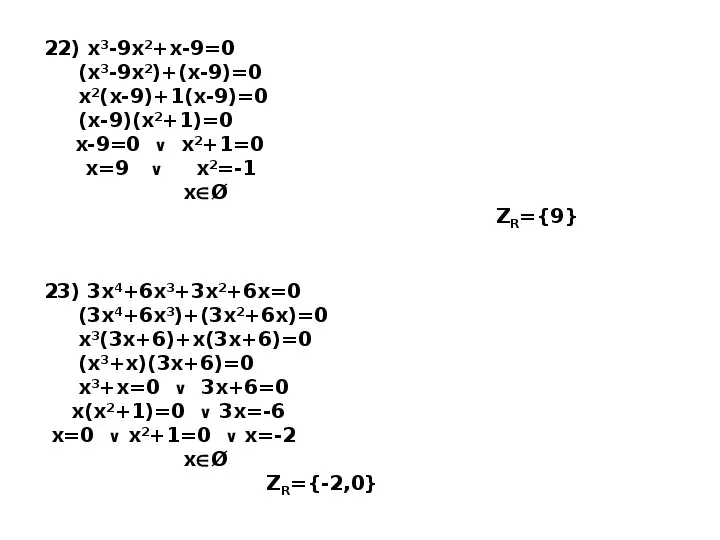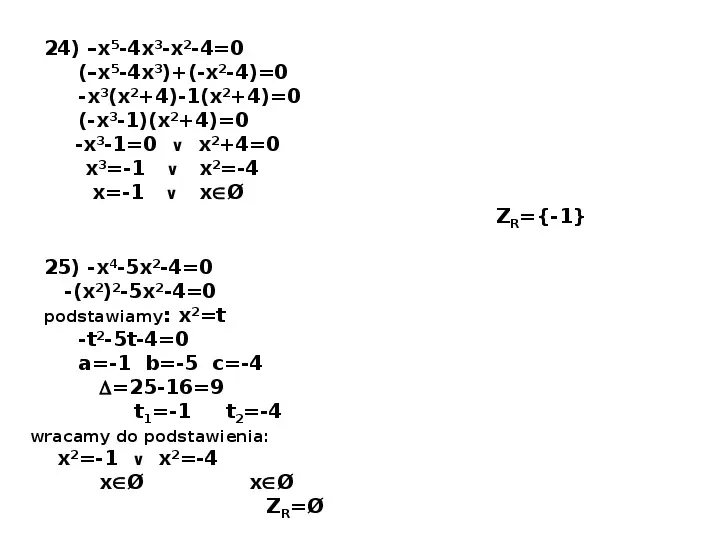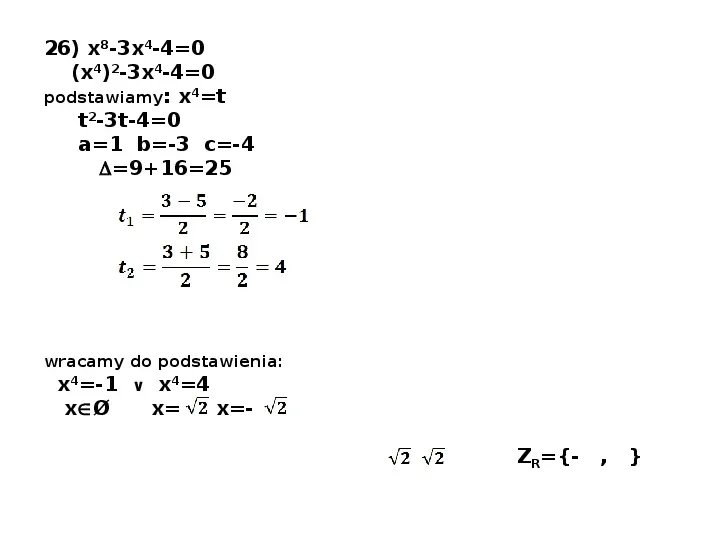Równania wielomianowe

Zobacz slidy

Treść prezentacji

Slide 1

RÓWNANIA WIELOMIANOWE

Slide 2

Równanie postaci W(x)0 gdzie W(x) jest wielomianem stopnia n nazywamy równaniem wielomianowym stopnia n. Liczba, która jest rozwiązaniem równania wielomianowego to pierwiastek (miejsce zerowe) wielomianu W(x). Aby rozwiązać równanie wielomianowe należy rozłożyć na czynniki wielomian i skorzystać z faktu, że iloczyn jest równy zero wtedy, gdy którykolwiek z czynników jest równy zero. ab0 a0 v b0

Slide 3

Zadanie: Rozwiąż równania: 1) 16x320 16x-32 x-2 ZR-2 2) (x-3)(3x9)0 x-30 3x90 x3 3x-9 x3 x-3 ZR-3,3 3) (4-x)(x7)(5x15)0 4-x0 x70 5x150 -x-4 x-7 5x-15 x4 x-7 x-3 ZR-7,-3,4

Slide 4

4) 16x(x-3)(x9)0 16x0 x-30 x90 x0 x3 x-9 ZR-9,0,3 5) (x-3)(3x9)0 x-30 3x90 x3 3x-9 x3 x-3 ZR-3,3 6) (4-x)(x26x)(5x5)0 4-x0 x26x0 5x50 -x-4 x(x6)0 5x-5 x4 x0 x60 x-1 x4 x0 x-6 x-1 ZR-6,-1,0,4

Slide 5

7) (x4)(2x-10)(x2-4)0 x40 2x-100 x2-40 x-4 2x10 x24 x-4 x5 x-2 x2 ZR-4,-2,2,5 8) (x2-9)(x2-6x)0 x2-90 x2-6x0 x29 x(x-6)0 x-3 x3 x0 x-60 x-3 x3 x0 x6 ZR-3,0,3,6 9) x2(x2-8x)(x10)0 x20 x2-8x0 x100 x0 x(x-8)0 x-10 x0 x0 x8 x-10 ZR-10,0,8

Slide 6

10) x2x40 a1 b1 c4 1-16-15 0 xØ ZR Ø 11) x26x50 a1 b6 c5 36-2016 x1-5 x2-1 ZR-5,-1 12) x35x24x0 x(x25x4)0 x0 x25x40 a1 b5 c4 25-169 x1-4 x2-1

Slide 7

13) x33x26x180 (x33x2)(6x18)0 x2(x3)6(x3)0 (x3)(x26)0 x30 x260 x-3 a1 b0 c6 0-24-24 0 xØ ZR-3 14) x3-8x2x-80 (x3-8x2)(x-8)0 x2(x-8)1(x-8)0 (x-8)(x21)0 x-80 x210 x8 a1 b0 c1 0-4-4 0 xØ Z 8

Slide 8

15) x3-9x0 x(x2-9)0 x0 x2-90 x29 x-3 x3 ZR-3,0,3 16) x3-x0 x(x2-1)0 x0 x2-10 x21 x-1 x1 ZR-1,0,1 17) x4-10 (x2)2-120 (x2-1)(x21)0 x2-10 x210 x21 x2-1 x-1 x1 xØ

Slide 9

18) 3x3-x2-21x70 (3x3-x2)(-21x7)0 x2(3x-1)-7(3x-1)0 (3x-1)(x2-7)0 3x-10 x2-70 3x1 x27 x x- x ZR,, 19) -2x3-5x28x200 (-2x3-5x2)(8x20)0 -x2(2x5)4(2x5)0 (2x5)(-x24)0 2x50 -x240 2x-5 x24 x-2 x-2 x2 ZR-2,-

Slide 10

20) 2x4x33x2x10 (2x4x3x2)(2x2x1)0 x2(2x2x1)1(2x2x1)0 (x21)(2x2x1)0 x210 2x2x10 x2-1 2x2x10 xØ a2 b1 c1 1-8-7 0 xØ ZRØ 21) 9x3-18x22x-40 (9x3-18x2)(2x-4)0 9x2(x-2)2(x-2)0 (x-2)(9x22)0 x-20 9x220 x2 a9 b0 c2 0-72-72 0 xØ ZR2

Slide 11

22) x3-9x2x-90 (x3-9x2)(x-9)0 x2(x-9)1(x-9)0 (x-9)(x21)0 x-90 x210 x9 x2-1 xØ ZR9 23) 3x46x33x26x0 (3x46x3)(3x26x)0 x3(3x6)x(3x6)0 (x3x)(3x6)0 x3x0 3x60 x(x21)0 3x-6 x0 x210 x-2 xØ ZR-2,0

Slide 12

24) x5-4x3-x2-40 (x5-4x3)(-x2-4)0 -x3(x24)-1(x24)0 (-x3-1)(x24)0 -x3-10 x240 x3-1 x2-4 x-1 xØ ZR-1 25) -x4-5x2-40 -(x2)2-5x2-40 podstawiamy: x2t -t2-5t-40 a-1 b-5 c-4 25-169 t1-1 t2-4 wracamy do podstawienia: x2-1 x2-4 xØ xØ ZRØ

Slide 13

26) x8-3x4-40 (x4)2-3x4-40 podstawiamy: x4t t2-3t-40 a1 b-3 c-4 91625 wracamy do podstawienia: x4-1 x44 xØ x xZR- ,