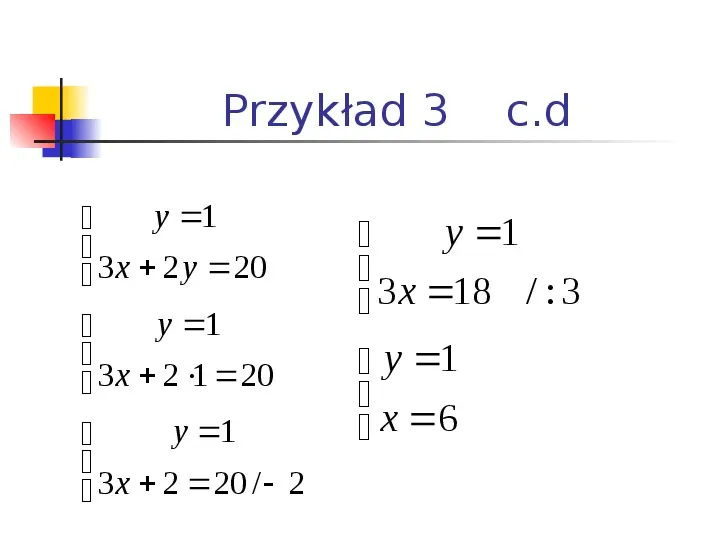Rozwiązywanie układów równań metodą przeciwnych współczynników

Zobacz slidy

Treść prezentacji

Slide 1

Rozwiązywanie układów równań metodą przeciwnych współczynników

Slide 2

Przykład 1 2 x 3 y 8 4 x 3 y 4 6 x 12 x 2 :6 Mamy gotowe przeciwne współczynniki Dodajemy stronami obydwa równania Otrzymujemy jedną niewiadomą

Slide 3

Przykład 1 x 2 2 x 3 y 8 x 2 2 2 3 y 8 x 2 4 3 y 8 c.d x 2 3 y 8 4 x 2 3 y 4 : 3 x 2 y 4 3 Otrzymaną niewiadomą x podstawiamy do dowolnego równania układu Obliczamy drugą niewiadomą y

Slide 4

Przykład 2 x 3 y 5 4 x 5 y 6 x 3 y 5 4 4 x 5 y 6 Musimy pomnożyć jedno równanie, aby mieć przeciwne współczynni ki

Slide 5

Przykład 2 4 x 12 y 20 4 x 5 y 6 7 y 14 : 7 y 2 c.d Dalej postępujemy tak samo jak w przykładzie 1

Slide 6

Przykład 2 y 2 x 3 y 5 y 2 x 3 ( 2) 5 c.d y 2 x 6 5 6 y 2 x 1

Slide 7

Przykład 3 4 x 5 y 19 3 3 x 2 y 20 4 12 x 15 y 57 12 x 8 y 80 Musimy pomnożyć oba równania, aby mieć przeciwne współczynni ki

Slide 8

Przykład 3 c.d 12 x 15 y 57 12 x 8 y 80 Dalej postępujemy jak w poprzednich przykładach 23 y 23 : 23 y 1

Slide 9

Przykład 3 y 1 3 x 2 y 20 y 1 3 x 2 1 20 y 1 3 x 2 20 2 c.d y 1 3x 18 : 3 y 1 x 6

Slide 10

Podsumowanie Metoda przeciwnych współczynników polega na takim przekształceniu jednego lub obu równań układu, aby przy tej samej niewiadomej uzyskać liczby będące liczbami przeciwnymi. Dodając stronami oba równania, eliminujemy jedną zmienną, dzięki czemu otrzymujemy równanie tylko z jedną niewiadomą. Po otrzymaniu jednej niewiadomej podstawiamy ją do dowolnego równania układu i obliczamy drugą niewiadomą.