Kinematyka

Zobacz slidy

Treść prezentacji

Slide 1

Kinematyka 1. 2. 3. 4. 5. 6. 7. Definicje podstawowe Wielkości pochodne Równania ruchu i toru Ruch prostoliniowy punktu materialnego 1. Na płaszczyźnie 2. W przestrzeni Ruch krzywoliniowy punktu materialnego 1. Na płaszczyźnie 2. W przestrzeni Ruch po okręgu Ruch ciała sztywnego 1. Postępowy 2. Obrotowy 3. Mieszany

Slide 2

Definicje podstawowe Kinematyka zajmuje się badaniem ilościowym ruchu ciał niezależnie od czynników fizycznych wywołujących ruch, jest więc pewnego rodzaju geometrią ruchu w czasie. Ciało doskonale sztywne stanowi przybliżony model ciała stałego i wystarczy dla rozwiązania niektórych ważnych dla zastosowań przypadków ruchu i równowagi. Ruchem ciała nazywamy zachodzącą w czasie zmianę jego położenia względem innego ciała, które umownie przyjmujemy za nieruchome. Układem odniesienia nazywamy układ związany z ciąłem nieruchomym nazywamy

Slide 3

Układy odniesienia Przestrzeń EUKLIDESOWA przestrzeń z określonym układem odniesienia związanym z ciałem nie poruszającym się.

Slide 4

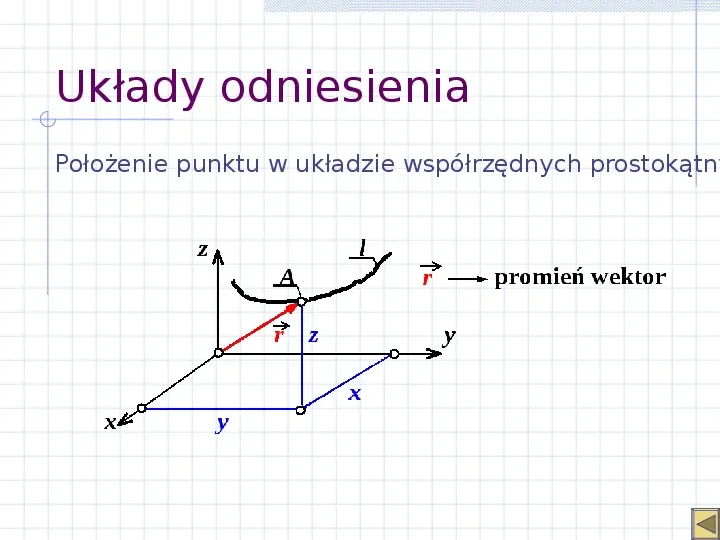
Układy odniesienia Położenie punktu w układzie współrzędnych prostokątny

Slide 5

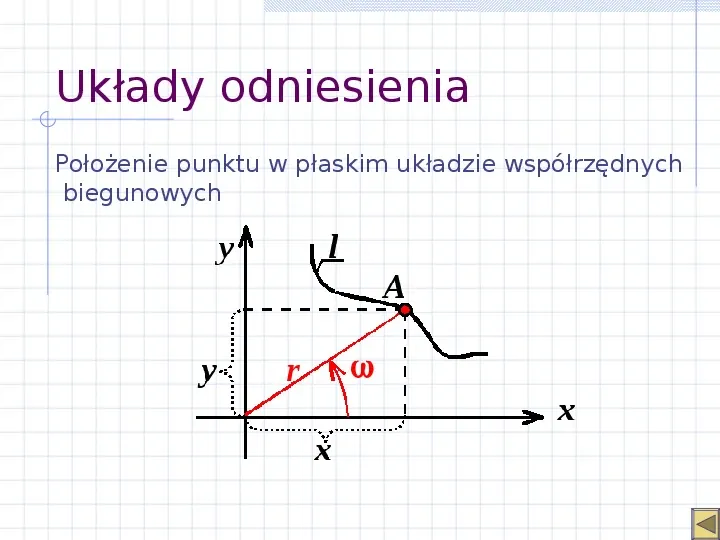
Układy odniesienia Położenie punktu w płaskim układzie współrzędnych biegunowych

Slide 6

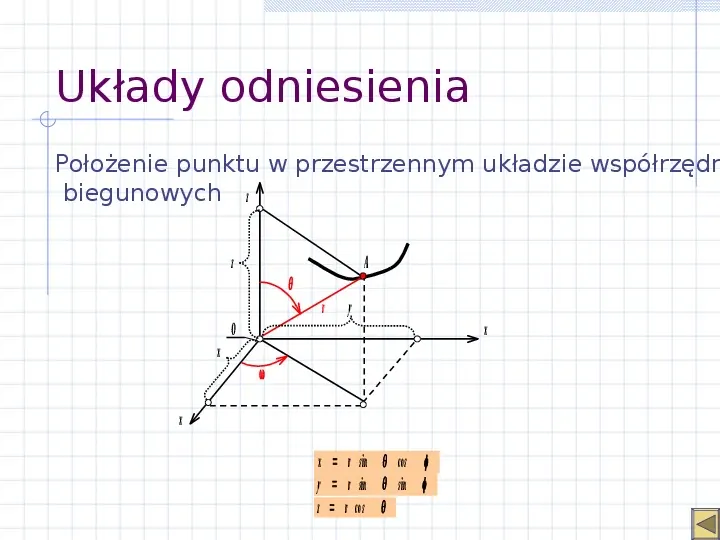
Układy odniesienia Położenie punktu w przestrzennym układzie współrzędn biegunowych z z A r y O x x x x r sin cos y r sin sin z r cos

Slide 7

Układy odniesienia Położenie punktu w przestrzennym układzie współrzędn walcowych

Slide 8

Położenie punktu y r rx ry ( x1 x0 ) x ( y1 y0 ) y A y1 r ry Kładziemy x00, y00 r x1 x y1y [ x1 , y1 ] y y 1 x , y 0 0 rx x x1 x 1 x

Slide 9

Prędkość i przyspieszenie Przypadek jednowymiarowy x Vśr t x dx V lim x dt t 0 t V aśr t V dV a lim x dt t 0 t Parametry są wektorami, tylko w przypadku rozpatrywa konkretnych kierunków można pominąć zapis wektorow

Slide 10

Równania ruchu Y Usuwamy więzy (pokazy) F X d r F m a m 2 dt 2

Slide 11

Równania ruchu Y Fx r0 y r0 r0 x Fy F X d 2 rx d 2 x Fx Fx m a x m 2 2 x x dt dt m d 2 x Fx Fx dx d dt 2 dt m m dt F dx Fx t C1 dx ( x t C1 )dt dt m m Fx 1 Fx 2 x tdt C1dt x t C21 C1t C22 m 2 m 1 Fx 2 x t C1t C2 2 m x x(t ) f (t )

Slide 12

Równania ruchu Ostatecznie dla dwóch współrzędnych otrzymujemy dwa równania parametryczne. W ten sposób otrzymuj układ równań, które nazywamy równaniami ruchu 1 Fx 2 x(t ) 2 m t C1x t C2 x y (t ) 1 Fy t 2 C t C 1y 2y 2 m

Slide 13

Równania ruchu Identyfikacja współczynników 1. II zasada dynamik 1 Fx 2 x ( t ) t C1x t C2 x 2 m y (t ) 1 Fy t 2 C t C 1y 2y 2 m Fx a x m Fy m a y 2. Współczynniki C?? wyznaczmy z warunków początko tzw. warunków brzegowych.

Slide 14

Równania ruchu 1 2 x ( t ) a x t C1x t C2 x 2 y (t ) 1 a t 2 C t C y 1y 2y 2 Identyfikacja współczynników t 0 V p , x p , y p Y Vp V py V px yp r0 y r0 r0 x Fy xp Fx F X Gdy x(t 0) x p t 0 y ( t 0 ) y p 1 x p a x 0 2 C1x 0 C2 x C2 x x p 2 1 y p a y 0 2 C1 y 0 C2 y C2 y y p 2

Slide 15

Równania ruchu Y 1 2 x ( t ) a x t C1x t C2 x 2 y (t ) 1 a t 2 C t C y 1y 2y 2 t 0 V p , x p , y p Identyfikacja współczynników Gdy t 0 V (t 0) V p V py Vp V px yp r0 y r0 r0 x Fy xp Fx F X Gdy Vx (t 0) V px t 0 V ( t 0 ) V py y dx Vx a x t C1x dt dy V y a y t C1 y dt

Slide 16

Równania ruchu 1 2 x ( t ) a x t C1x t C2 x 2 y (t ) 1 a t 2 C t C y 1y 2y 2 Identyfikacja t 0 V p , x p , y p współczynników Y Vp V py V px yp r0 y r0 r0 x Fy xp Fx F X Vx (t 0) a x 0 C1x C1x V px V y (t 0) a y 0 C1 y C1 y V py

Slide 17

Równania ruchu 1 2 x ( t ) a x t C1x t C2 x 2 y (t ) 1 a t 2 C t C y 1y 2y 2 t 0 V p , x p , y p Identyfikacja współczynników zestawienie końcowe 1 2 x(t ) 2 a x t V px t x p y (t ) 1 a t 2 V t y y py p 2 Dla układu przestrzennego 1 2 z (t ) a z t V pz t z p 2 Przykład rzut poziomy

Slide 18

Równie toru y x x(t ) y y (t ) z z (t ) z f ( x, y ) 2D x x(t ) y y (t ) x y f (x) Przykład cd z

Slide 19

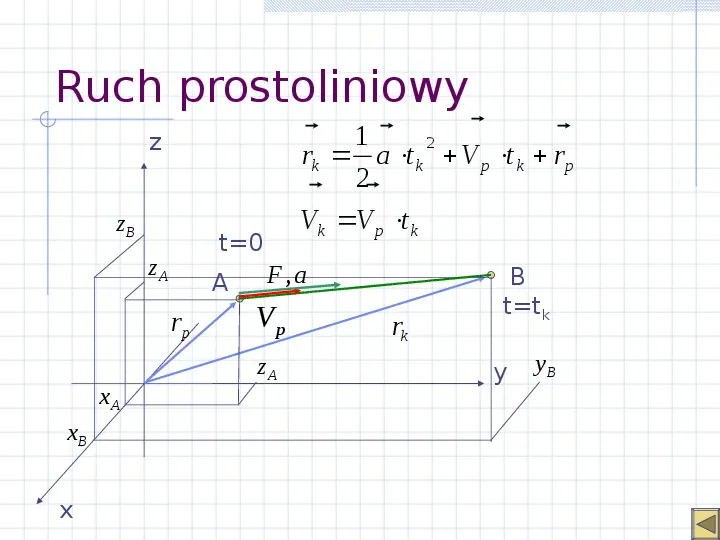
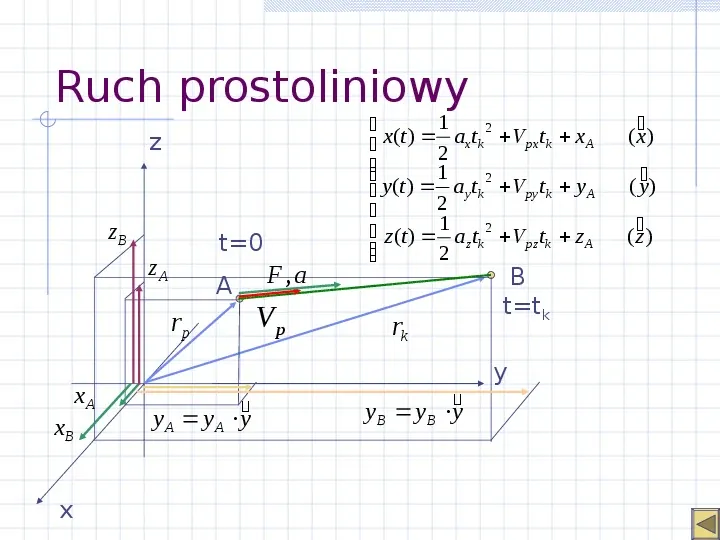
Ruch prostoliniowy 1 2 rk a t k V p t k rp 2 Vk V p t k z zB zA rp xA xB x t0 F, a A Vp zA rk B ttk y yB

Slide 20

Ruch prostoliniowy z zB zA rp xB x xA t0 F, a A y A y A y Vp 1 2 x ( t ) a t x k V px t k x A 2 1 2 y ( t ) a t y k V py t k y A 2 z (t ) 1 a z t k 2 V pz t k z A 2 rk y B y B y B ttk y (x) ( y) (z )

Slide 21

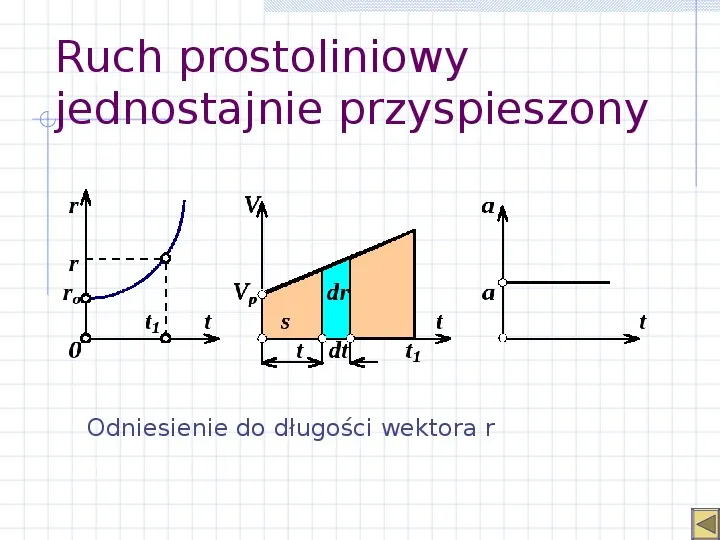
Ruch prostoliniowy jednostajnie przyspieszony Odniesienie do długości wektora r

Slide 22

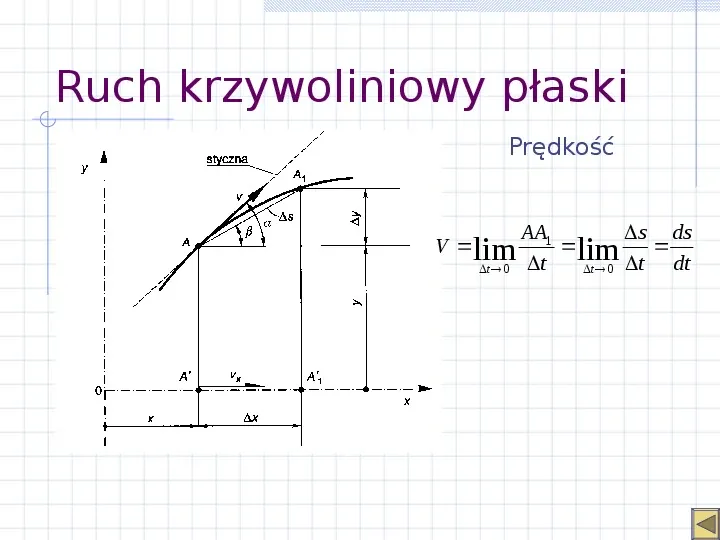
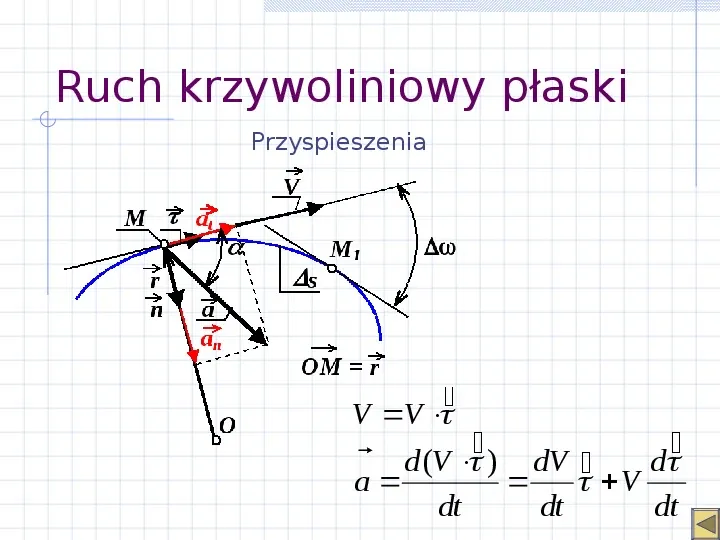
Ruch krzywoliniowy płaski Prędkość AA1 s ds V lim lim dt t 0 t t 0 t

Slide 23

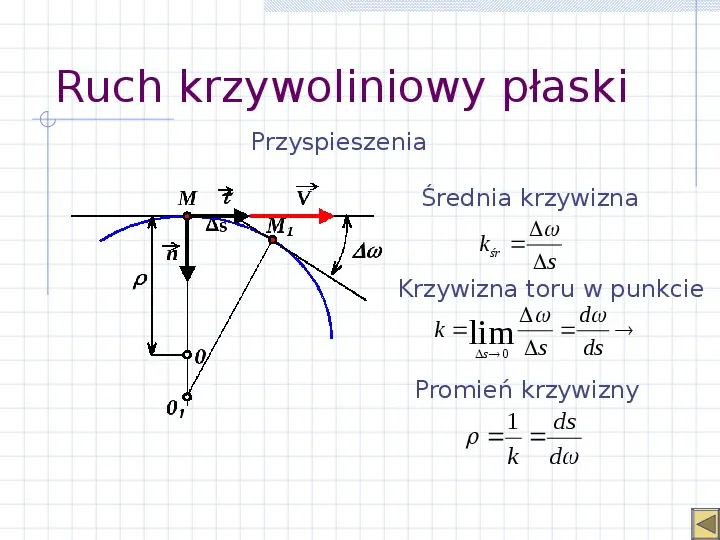
Ruch krzywoliniowy płaski Przyspieszenia Średnia krzywizna k śr s Krzywizna toru w punkcie d k lim ds s 0 s Promień krzywizny 1 ds k d

Slide 24

Ruch krzywoliniowy płaski Przyspieszenia V V d (V ) dV d a V dt dt dt

Slide 25

Ruch krzywoliniowy płaski Przyspieszenia Przyrost wersora 2 sin 2 2 2 sin sin 2 d 1d d lim 0 2 2 dV d d d a V n n dt dt dt dt ds V dt d 1 ds dV ds d a V n dt dt ds 2 dV V a n at an dt

Slide 26

Ruch punktu po okręgu s 2 2r s r d ds d r 1 mg d z i e s r V s r s dtdt dt

Slide 27

Ruch punktu po okręgu d d 2 dV d d dt at r r r r 2 dt dt dt dt V2 an 2 r r 2 d 4 a a a r dt 2 t 2 n

Slide 28

Ruch punktu po okręgu we współrzędnych biegunowych V dr V r d a a V V r V r 2 r 2 V V V ar dt dt V tg Vr r Rachunki wektorowe Założenie rconst dV d d dr a r r dt dt dt dt a r V V r 2 V a r r 2 r r

Slide 29

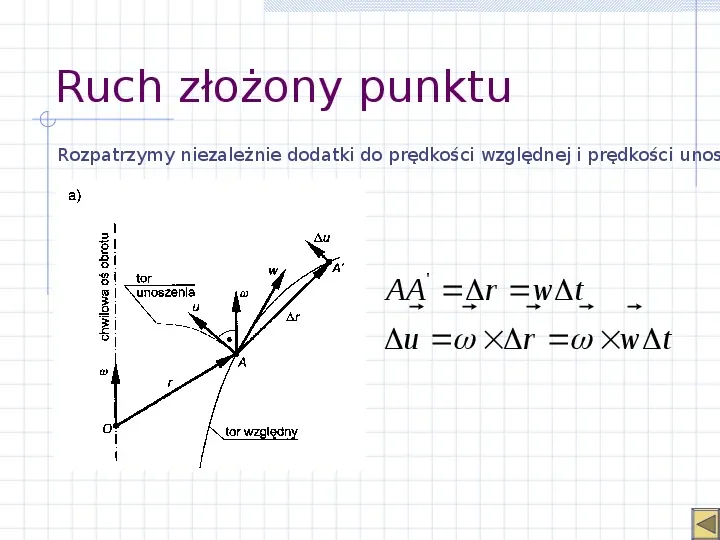
Ruch złożony punktu AA w lim t 0 t Prędkość względna punktu A BB u lim 1 t 0 t Prędkość unoszenia punktu A AA v lim 1 t 0 t Prędkość bezwzględna punktu A v u w

Slide 30

Ruch złożony punktu Rozpatrzymy niezależnie dodatki do prędkości względnej i prędkości unos AA r wt u r wt

Slide 31

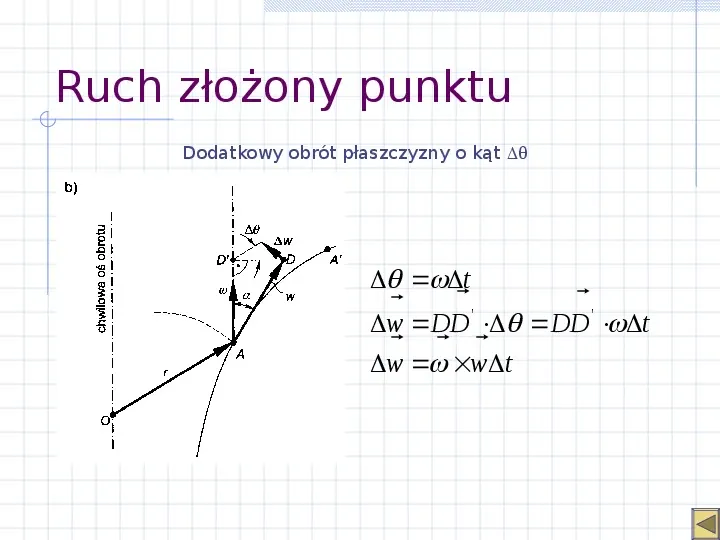
Ruch złożony punktu Dodatkowy obrót płaszczyzny o kąt t w DD DD t w wt

Slide 32

Ruch złożony punktu Uzyskujemy wynik przyspieszenia dodatkowego jako superpozycje przyrostów prędkości względnej i unoszenia u w w w t ac lim lim 2 w t 0 t 0 t t Przyspieszenie to nosi nazwę przyspieszenie Coriolisa

Slide 33

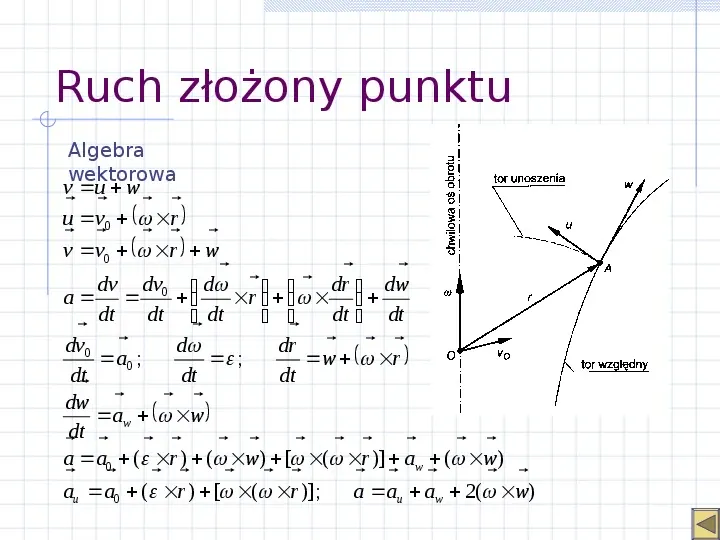
Ruch złożony punktu Algebra wektorowa v u w u v0 r v v0 r w dv dv0 d dr dw a r dt dt dt dt dt dv0 d dr a0 ; ; w r dt dt dt dw aw w dt a a0 ( r ) ( w) [ ( r )] aw ( w) au a0 ( r ) [ ( r )] ; a au aw 2( w)

Slide 34

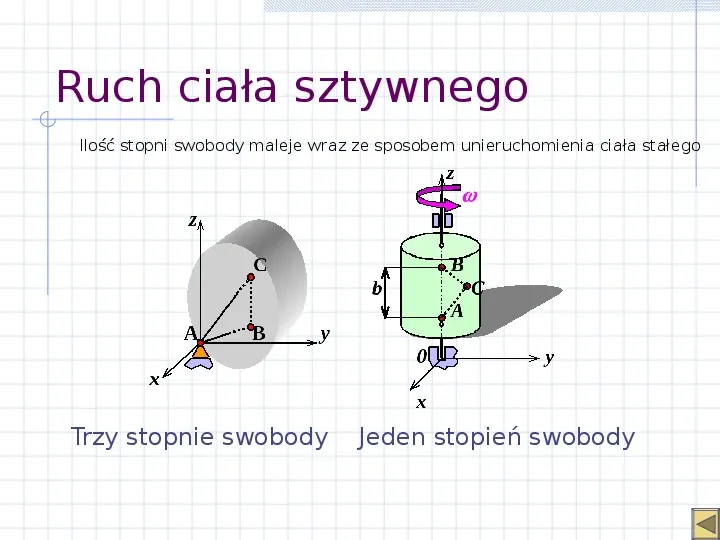
Ruch ciała sztywnego rB rA b, d rC - rA c, rC - rB (xA xB)2 (yA yB)2 (zA zB)2 b2 (xA xC)2 (yA yC)2 (zA zC)2 c2 (xB xC)2 (yB yC)2 (zB zC)2 d2 Aby określić położenie ciała w przestrzeni należy określić sześć niezależnych współrzę

Slide 35

Ruch ciała sztywnego Ilość stopni swobody maleje wraz ze sposobem unieruchomienia ciała stałego Trzy stopnie swobody Jeden stopień swobody

Slide 36

Ruch ciała sztywnego W ciele sztywnym podczas dowolnego ruchu, rzuty wektorów prędkości dwóch jej dowolnych punktów na prostą łączącą te punkty są sobie równe. r rB rA dr drB drA VB VA dt dt dt dr r (VB V A ) r dt dr d dr dr (r r ) r r 2r 0 dt dt dt dt VB r VA r VA r VA r cos r r rr cos 0o r 2 const 0 (VB VA ) r VB r VB r cos

Slide 37

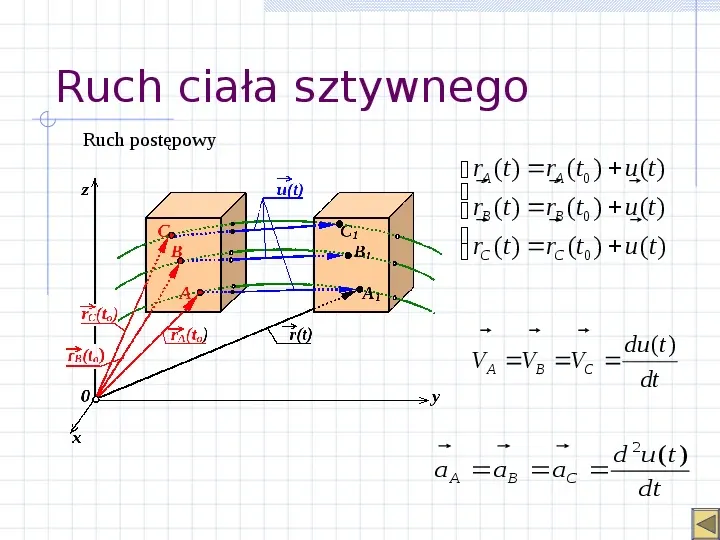
Ruch ciała sztywnego Ruch postępowy rA (t ) rA (t0 ) u (t ) rB (t ) rB (t0 ) u (t ) r (t ) r (t ) u(t ) C 0 C du(t ) VA VB VC dt d u (t ) a A a B aC dt 2

Slide 38

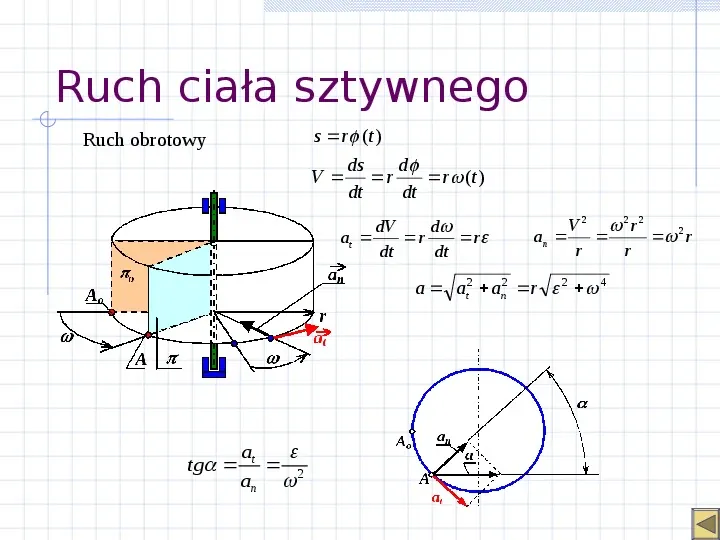
Ruch ciała sztywnego s r (t ) ds d V r r (t ) dt dt Ruch obrotowy dV d at r r dt dt V 2 2r 2 an 2 r r r a at2 an2 r 2 4 tg at 2 an