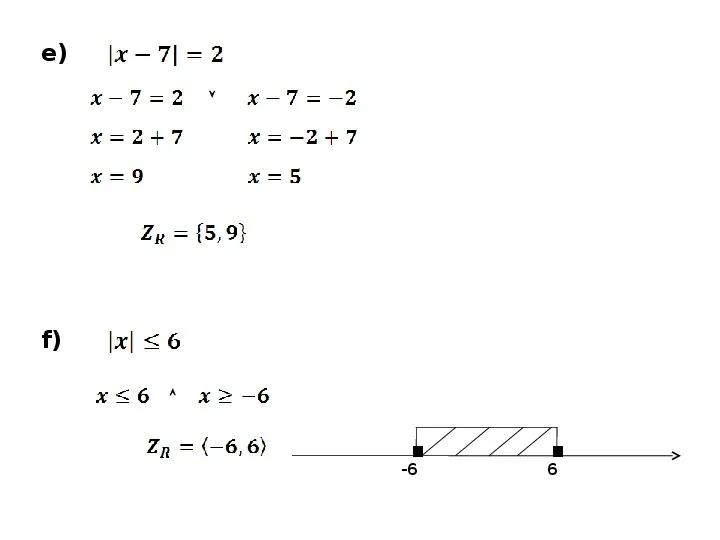Równania, nierówności z wartością bezwzględną

Zobacz slidy

Treść prezentacji

Slide 1

RÓWNANIA NIERÓWNOŚCI Z WARTOŚCIĄ BEZWZGLĘDNĄ

Slide 2

Najpierw zapiszemy definicję wartości bezwzględnej oraz własności związane z wartością bezwzględną wykorzystane w zadaniach:

Slide 3

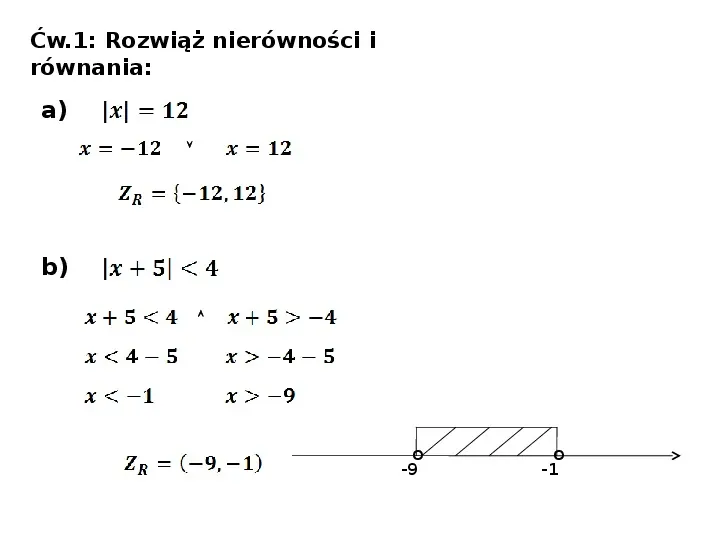
Ćw.1: Rozwiąż nierówności i równania: a) b) o -9 o -1

Slide 4

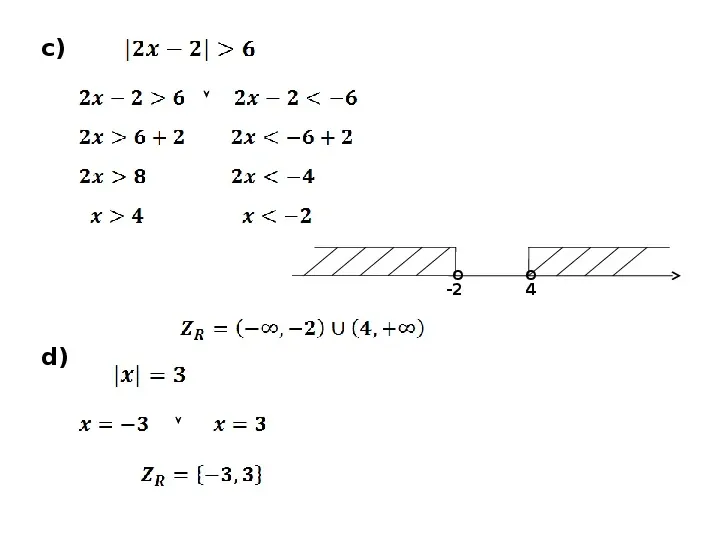
c) o -2 d) o 4

Slide 5

e) f) -6 6

Slide 6

g) 5x22x-80 a5 b2 c-8 Δ b2-4ac Δ 22-45(-8)4160164 Δ 0 - wyznaczamy dwa rozwiązania:

Slide 7

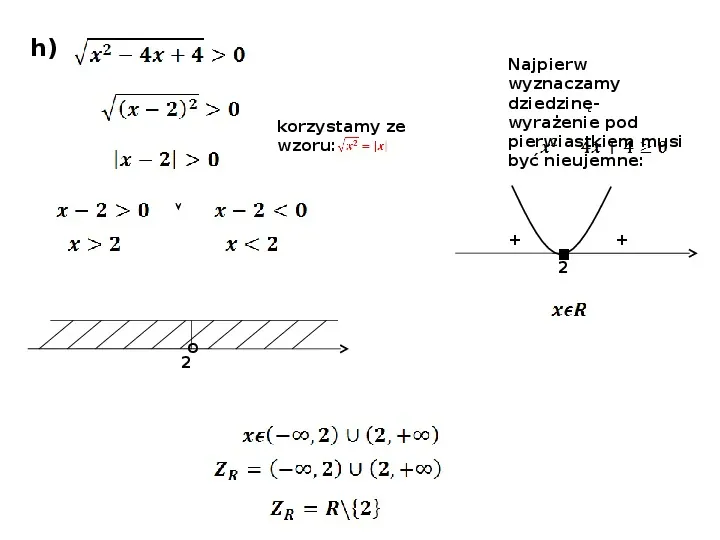
h) korzystamy ze wzoru: Najpierw wyznaczamy dziedzinęwyrażenie pod pierwiastkiem musi być nieujemne: 2 o 2

Slide 8

i) a1 Δ Δ Δ Δ b-2 c-3 b2-4ac (-2)2-41(-3) 41216 0 dwa rozwiązania a1 b-2 c3 Δ b2-4ac Δ (-2)2-413 Δ 4-12-8 Δ 0 brak rozwiązań

Slide 9

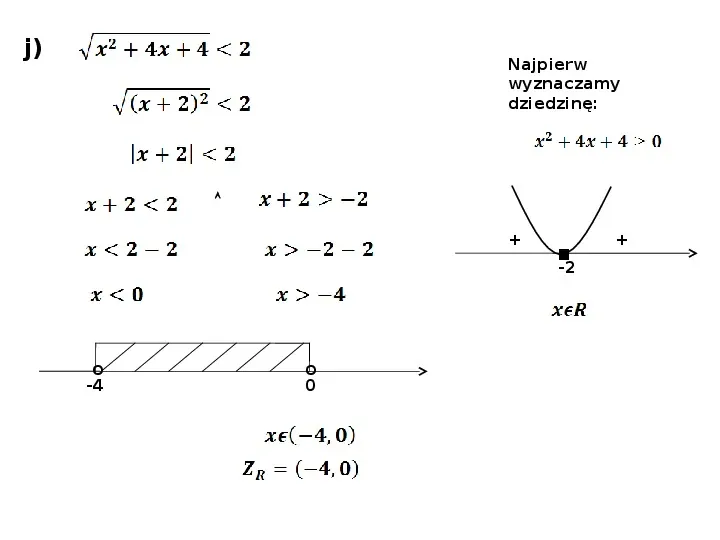
j) Najpierw wyznaczamy dziedzinę: -2 o -4 o 0

Slide 10

k) Najpierw wyznaczamy dziedzinę: -4

Slide 11

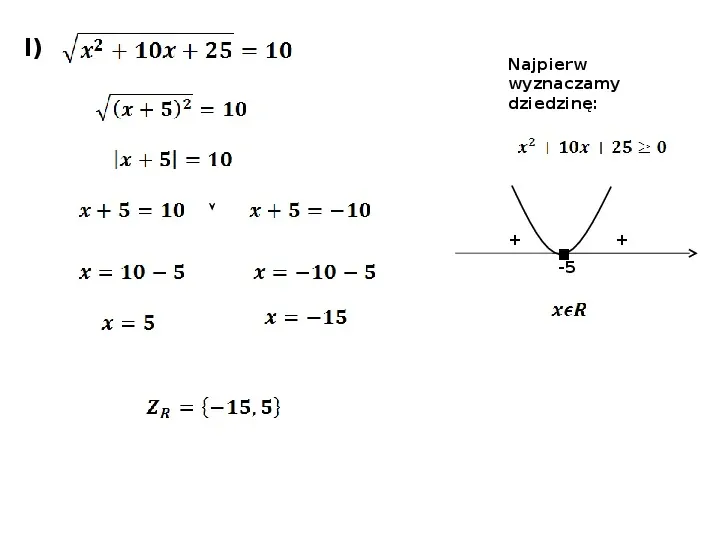
l) Najpierw wyznaczamy dziedzinę: -5

Slide 12

m ) Najpierw wyznaczamy dziedzinę: 3

Slide 13

n) Wyznaczone wyżej miejsca zerowe podzieliły zbiór liczb rzeczywistych na trzy przedziały, dlatego rozpatrujemy trzy przypadki: 1) 2) 0 2 x 3)

Slide 14

o) Wyznaczone wyżej miejsca zerowe podzieliły zbiór liczb rzeczywistych na trzy przedziały, dlatego rozpatrujemy trzy przypadki: 1) 2) -2 1 x 3) Otrzymaliśmy trzy liczby, ale żadna z nich nie należy do zapisanych wyżej przedziałów. Równanie to nie ma rozwiązania.

Slide 15

Ćw.2: Dana jest funkcja: f(x)x25x4. Dla jakiej wartości funkcja yf(x) przyjmuje wartości równe zero? Rozwiąż nierówność: f(x)-40. a1 Δ Δ Δ b5 c4 b2-4ac 52-41425-169 0 - wyznaczamy dwa miejsca zerowe Funkcja przyjmuje wartości równe zero dla argumentów -4 oraz -1.

Slide 16

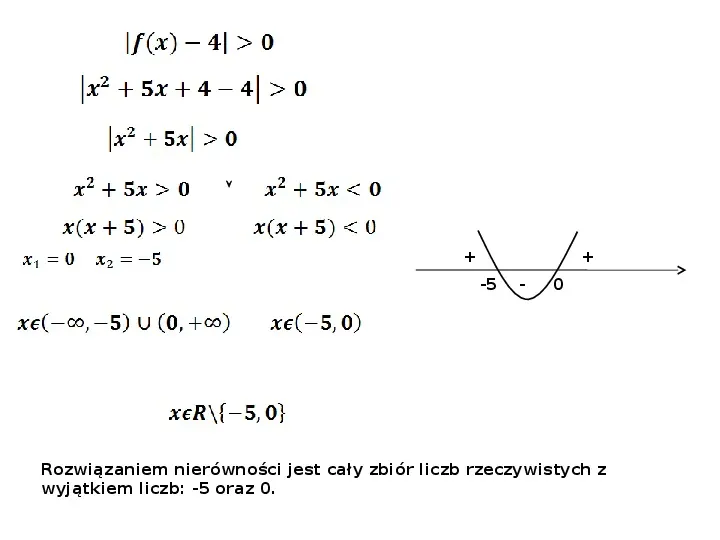
-5 - 0 Rozwiązaniem nierówności jest cały zbiór liczb rzeczywistych z wyjątkiem liczb: -5 oraz 0.