Układy współrzędnych, odwzorowania kartograficzne wprowadzenie do algorytmów gis

Zobacz slidy

Treść prezentacji

Slide 1

GIS SYSTEMY INFORMACJI GEOGRAFICZNEJ UKŁADY WSPÓŁRZĘDNYCH, ODWZOROWANIA KARTOGRAFICZNE WPROWADZENIE DO ALGORYTMÓW GIS

Slide 2

PLAN PREZENTACJI 1. Współrzędne geograficzne, elipsoidalne, powszechnie stosowane elipsoidy,układy odniesienia 2. Odwzorowania kartograficzne definicja podział, odwzorowania wiernokątne, wiernopolowe, wiernoodległościowe 3. Algorytmy upraszczania danych, algorytm Douglas-Peucker, algorytm redukcji liczby wierzchołków 4. Pojęcie przestrzeni wektorowej, odległości, normy wektora, iloczynu skalarnego, przykłady przestrzeni wektorowych, podprzestrzeni wektorowych 5. Reprezentacje prostych, krzywych, odległość punktu od prostej 6. Wielomiany Newtona, Lagrangea, Hermitea, Bernsteina 7. Algorytm wygładzania linii z wykorzystaniem Active Contours (Snakes)

Slide 3

MAPY DEFINICJA Mapa (z łac. mappa obrus) - uogólniony obraz powierzchni Ziemi lub jej części (także nieba lub planety czy innego ciała niebieskiego), wykonywany na płaszczyźnie, w skali, według zasad odwzorowania kartograficznego, przy użyciu znaków graficznych. Mapa stanowi podstawowe narzędzie badań i prezentacji wyników m.in. w historii, geografii i geodezji. Mapa jest to obraz fizycznej powierzchni ziemi na płaszczyźnie w przyjętym odwzorowaniu kartograficznym i założonej skali z symbolicznym przedstawieniem obiektów i ukształtowania. Treść map - znaki umowne, punkty wysokościowe (pikiety), warstwice, siatka współrzędnych, opisy. Skala mapy zależność pomiędzy długością odcinka łączącego 2 punkty na mapie i odległością odpowiadających im punktów na powierzchni odniesienia 1 : M.

Slide 5

UKŁAD WSPÓŁRZĘDNYCH GEOGRAFICZNYCH

Slide 6

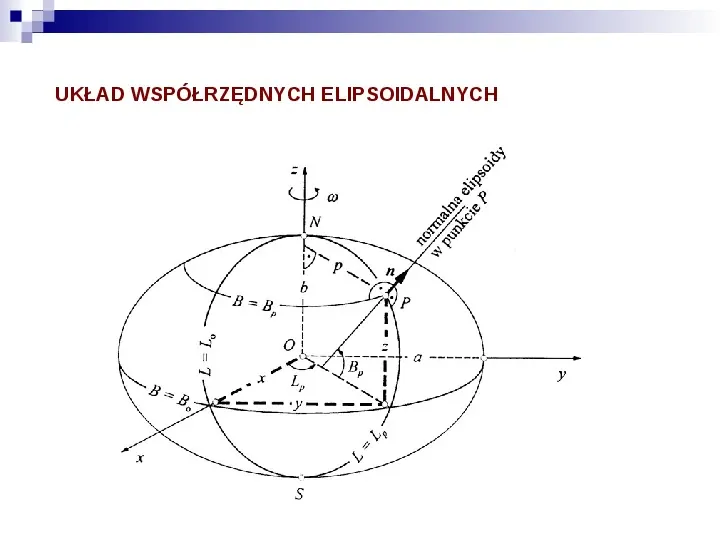
UKŁAD WSPÓŁRZĘDNYCH ELIPSOIDALNYCH

Slide 7

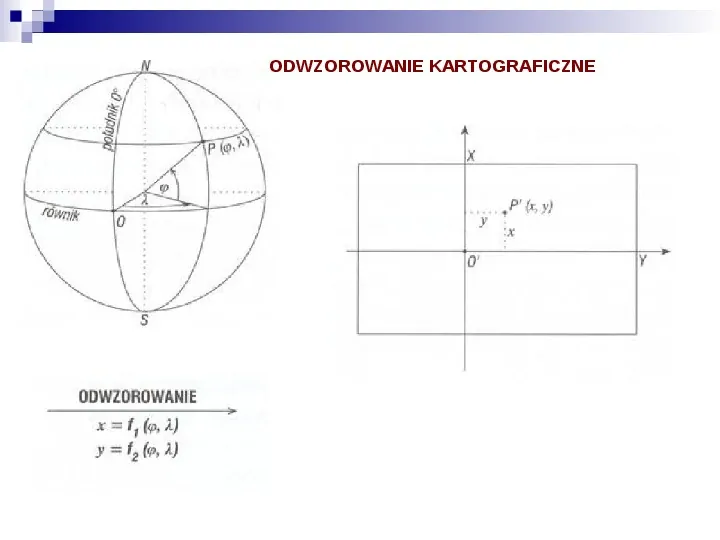
ODWZOROWANIE KARTOGRAFICZNE

Slide 8

ODWZOROWANIE POWIERZCHNI W POWIERZCHNIĘ Odwzorowaniem jednej powierzchni w drugą nazywamy każdą wzajemnie jednoznaczną odpowiedniość punktową między powierzchnią nazywaną oryginałem a powierzchnią nazywaną obrazem. Odwzorowanie kartograficzne jest umownym, określonym matematycznie sposobem przyporządkowania punktom powierzchni elipsoidy (lub kuli) punktów na płaszczyźnie. W zastosowaniach GIS (tym kartografii) powierzchnia oryginału i powierzchnia obrazu są powierzchniami regularnymi. W odwzorowaniach regularnych: obrazem punktu jest punkt obrazem krzywej jest krzywa obrazem kąta jest kąt obrazem powierzchni jest powierzchnia

Slide 9

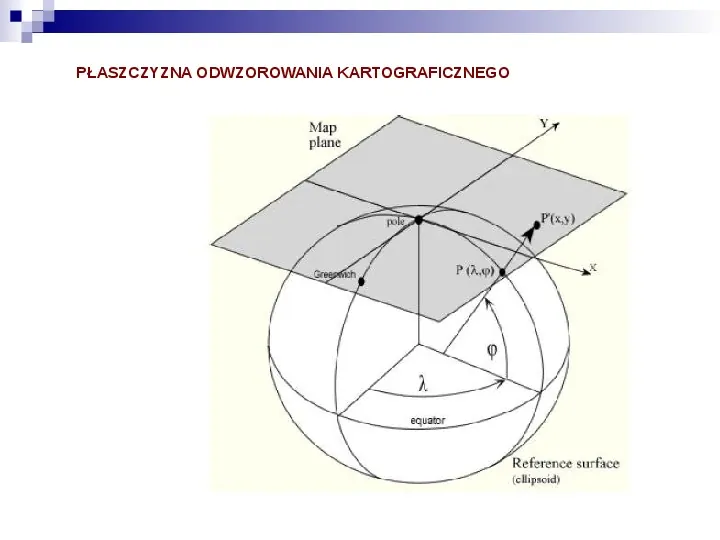
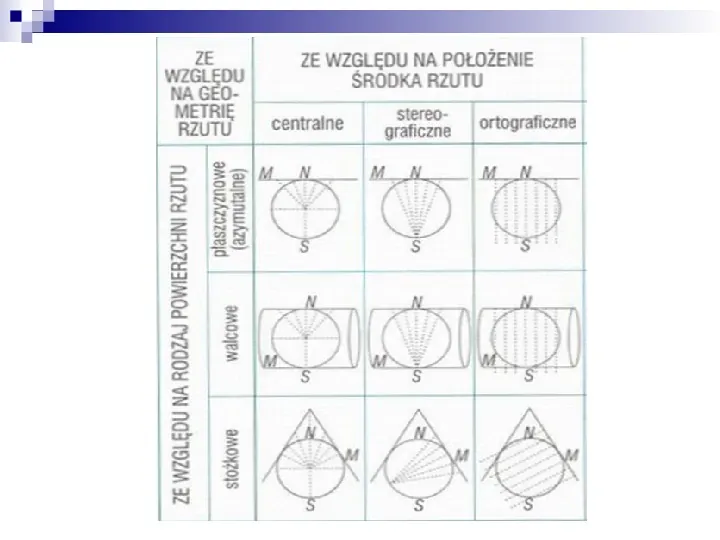
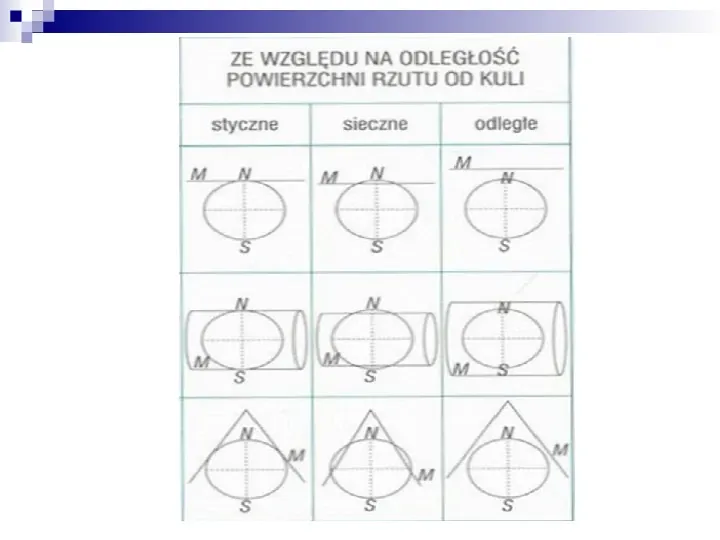
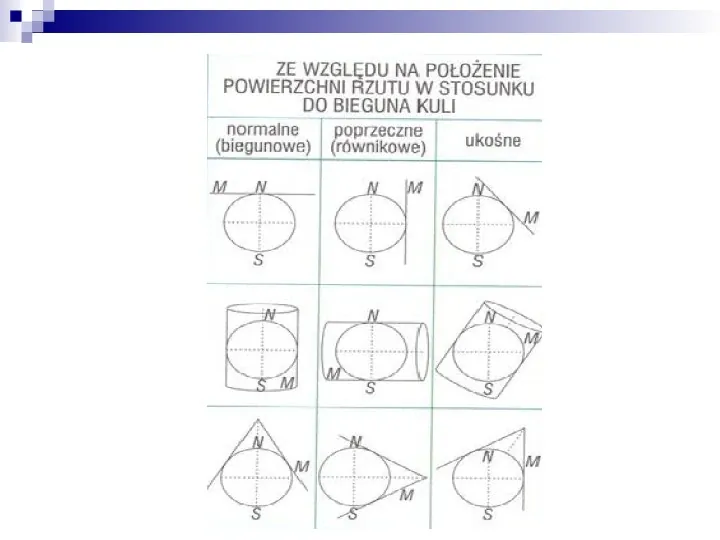
PŁASZCZYZNA ODWZOROWANIA KARTOGRAFICZNEGO

Slide 13

PODSTAWOWE ODWZOROWANIA KARTOGRAFICZNE Wybór odwzorowania dla map uwzględnia przede wszystkim kryterium występujących na mapie zniekształceń odwzorowawczych. Według tego kryterium można wyróżnić odwzorowania: wiernokątne, mBmL wiernopolowe, mBmL1 wiernoodległościowe, mB1, lub mL1 dowolne

Slide 14

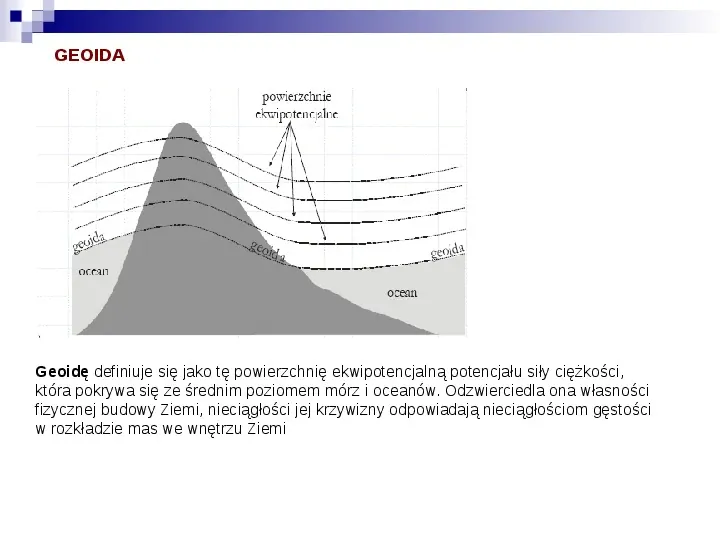
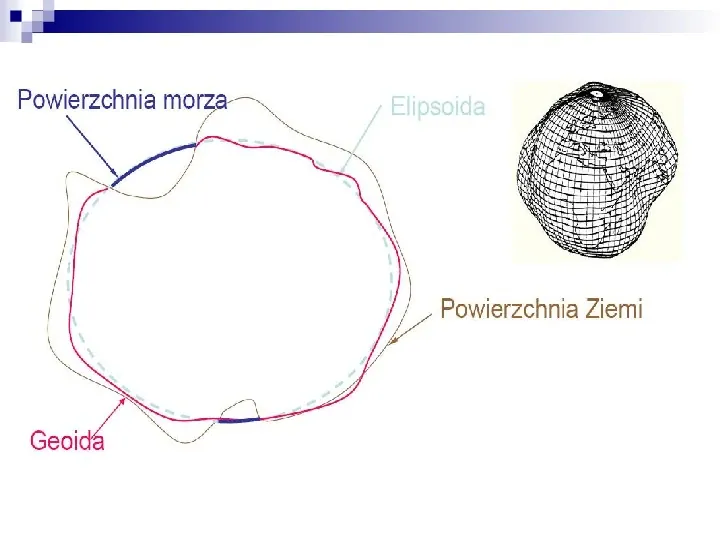
GEOIDA Geoidę definiuje się jako tę powierzchnię ekwipotencjalną potencjału siły ciężkości, która pokrywa się ze średnim poziomem mórz i oceanów. Odzwierciedla ona własności fizycznej budowy Ziemi, nieciągłości jej krzywizny odpowiadają nieciągłościom gęstości w rozkładzie mas we wnętrzu Ziemi

Slide 16

PRZYŚPIESZENIE ZIEMSKIE

Slide 17

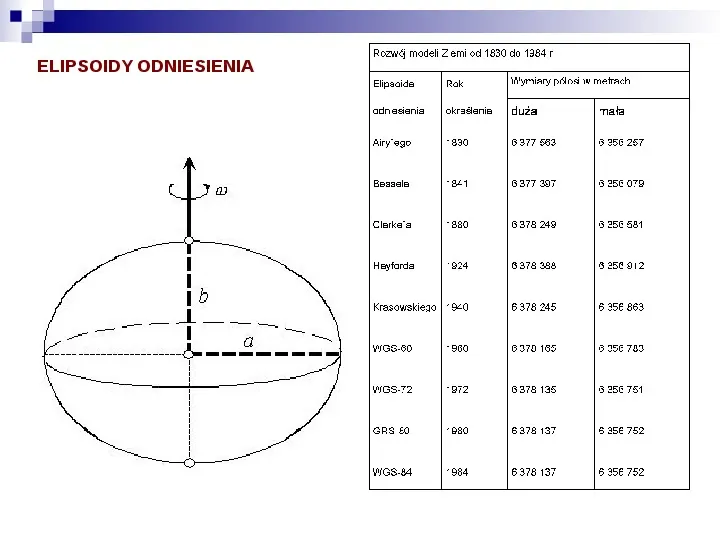
ELIPSOIDY ODNIESIENIA

Slide 18

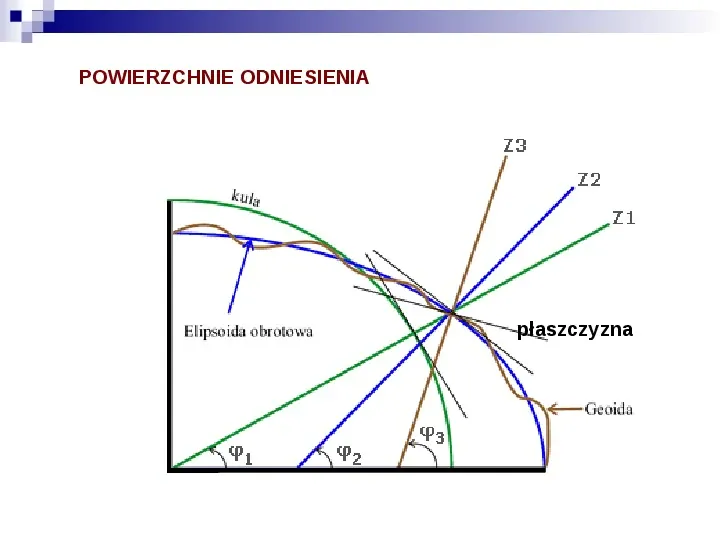
POWIERZCHNIE ODNIESIENIA płaszczyzna

Slide 19

POWIERZCHNIE ODNIESIENIA I WSPÓŁRZĘDNE Szerokość geodezyjna B punktu na elipsoidzie i jej związek z szerokością geograficzną na kuli.

Slide 20

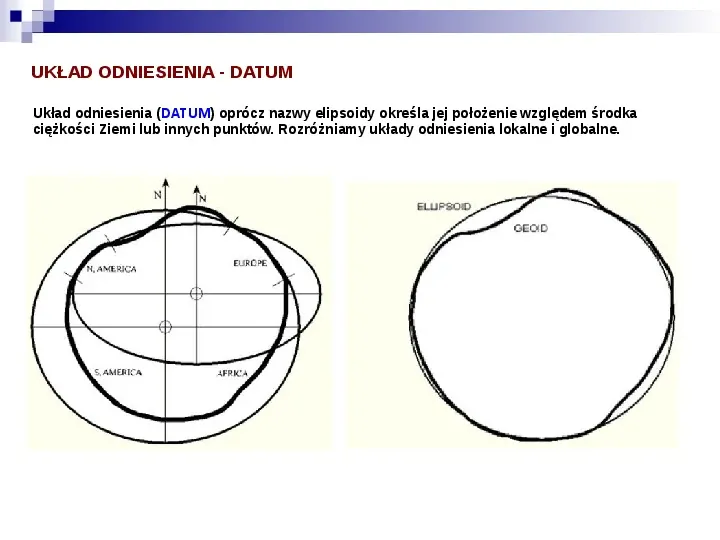
UKŁAD ODNIESIENIA - DATUM Układ odniesienia (DATUM) oprócz nazwy elipsoidy określa jej położenie względem środka ciężkości Ziemi lub innych punktów. Rozróżniamy układy odniesienia lokalne i globalne.

Slide 21

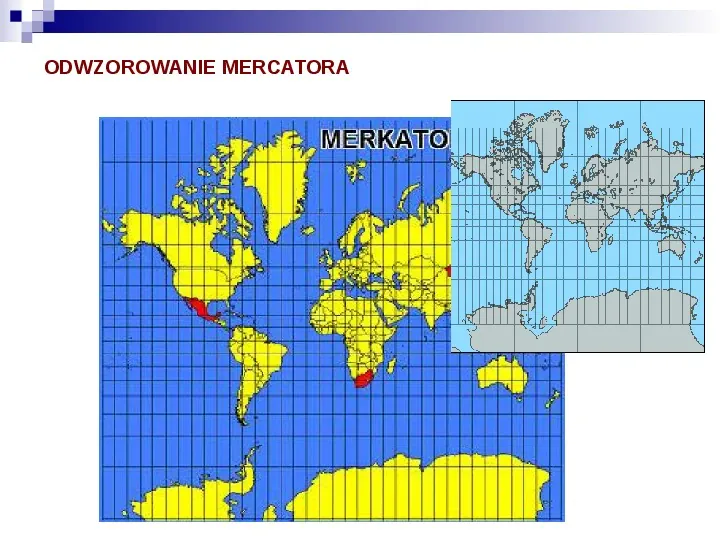
ODWZOROWANIE MERCATORA

Slide 23

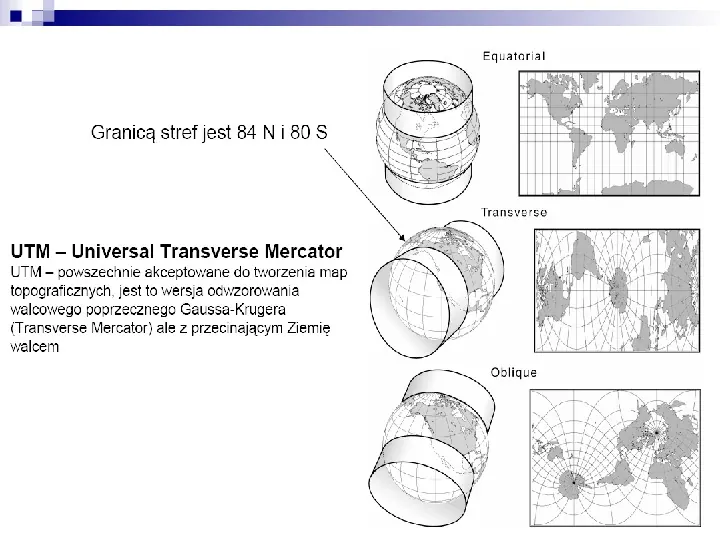
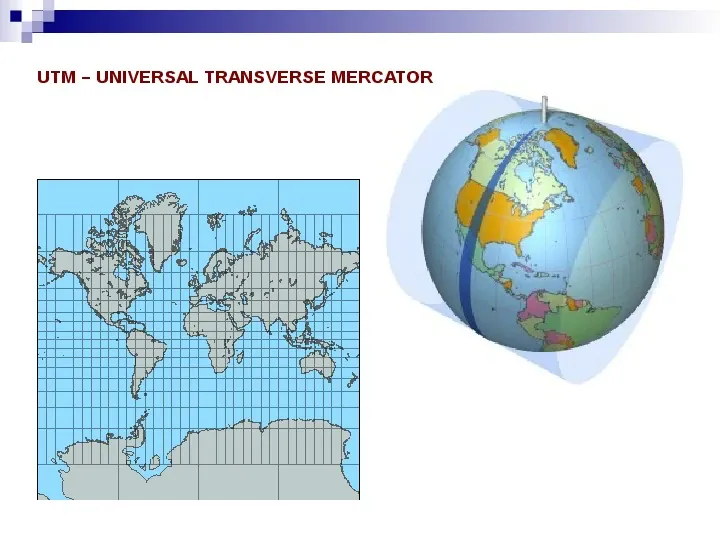
UTM UNIVERSAL TRANSVERSE MERCATOR

Slide 24

ODWZOROWANIA WIERNOKĄTNE Odwzorowanie kartograficzne oddające wszystkie właściwości oryginalnej sfery powinien być dokładnie perfekcyjnie równoodległe, to znaczy odległości między dowolnymi dwoma punktami powinny zachowywać ten sam stosunek zarówno na mapie i na sferze. W ten sposób, także wszystkie kształty zostają zachowane. Mapa na płaszczyźnie nie może spełnić tej właściwości (np. punkty na krawędzi mapy). W wielu zastosowaniach kartograficznych oraz pewnych rodzajach nawigacji słabszy warunek poprawność kształtu jest najbardziej podstawowym wymaganiem. Kąt między dowolnymi dwoma liniami na sferze musi być taki sam jak kąt między tymi liniami w odwzorowaniu kartograficznym na mapie. W szczególności, wszystkie południki muszą przecinać równoleżniki pod kątem prostym. Ponadto skala w dowolnym punkcie musi być taka sama we wszystkich kierunkach. Wiernokątność jest ściśle lokalną właściwością: kąty (a zatem i kształt) nie mogą być zachowane w dalszej odległości od punktu przecięcia. W rzeczywistości linie proste na sferze zostają odwzorowane jako linie zakrzywione na płaszczyźnie i odwrotnie. Odwzorowania równokątne znajdują zastosowanie w odwzorowaniach wielkoskalowych, natomiast są rzadko stosowane w mapach całych kontynentów lub świata. Ponieważ odwzorowanie równokątne nie może być jednocześnie wiernopolowym, odwzorowania wiernokątne nie są stosowane w zastosowaniach statystycznych, gdzie porównanie rozmiaru jest powszechnie wykonywaną operacją.

Slide 25

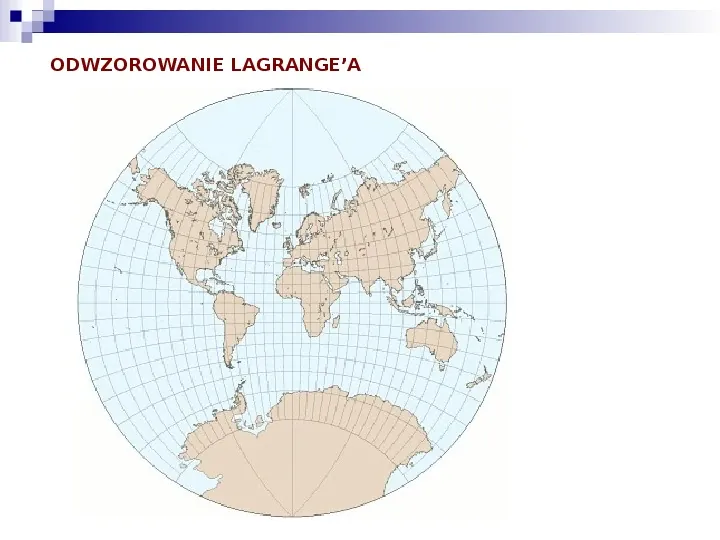
ODWZOROWANIA WIERNOKĄTNE STANDARDOWE Podstawowe odwzorowania wiernokątne: Stereograficzne płaszczyznowe, zachowujące kształt każdego okręgu na sferze Odwzorowanie Merkatora, walcowe w normalnym aspekcie posiada proste, pionowe południki, umożliwiając bezpośredni pomiary położenia szerokości geograficznej Odwzorowanie równokątne stożkowe, ogólny przypadek odwzorowania Punkty osobliwe: punkty odwzorowane w nieskończoności punkty, gdzie nie jest zachowana równokątność W szczególności (w aspekcie normalnym), odwzorowanie stereograficzne płaszczyznowe nie odwzorowuje punktu przeciwległego środkowi odwzorowania. Odwzorowanie Mercatora nie obejmuje dwu biegunów, a odwzorowanie stożkowe równokątne z pojedynczym biegunem, nie zachowującym równokątności (ponieważ suma kątów wszystkich południków jest mniejsza od 360 stopni). ODWZOROWANIE LAGRANGEA W roku 1772, Joann Lambert przedstawił odwzorowanie wiernokątne o następujących właściwościach: na sferze, odległości południków zmniejszano o czynnik n na sferze zmienia się odległości między równoleżnikami w celu uzyskania równokątności zastosowanie odwzorowania płaszczyznowego stereograficznego w aspekcie równikowym Lambert przedstawił ogólny przypadek dla dowolnego n i centralnego równoleżnika, najczęściej wykorzystywany przypadek dla równika z n 0.5 znany jest pod nazwą odwzorowania Lagrangea. Joseph Lagrangea uogólnił odwzorowanie na przypadek elipsoidy. Odwzorowanie Lagrangea przedstawia cały świat na powierzchni okręgu. Z powodu zastosowania odwzorowania stereograficznego, wszystkie południki i równoleżniki są łukami okręgów ( środkowy południk i równoleżnik jest linią prostą). Skala zostaje silnie zniekształcona przy biegunach. Odwzorowanie rzadko stosowane praktycznie, jednakże stanowi podstawę szeregu pochodnych odwzorowań równokątnych, gdyż odwzorowanie sfery na koło jest fundamentalnym krokiem w tworzeniu odwzorowania wiernokątnego.

Slide 26

ODWZOROWANIE LAGRANGEA

Slide 27

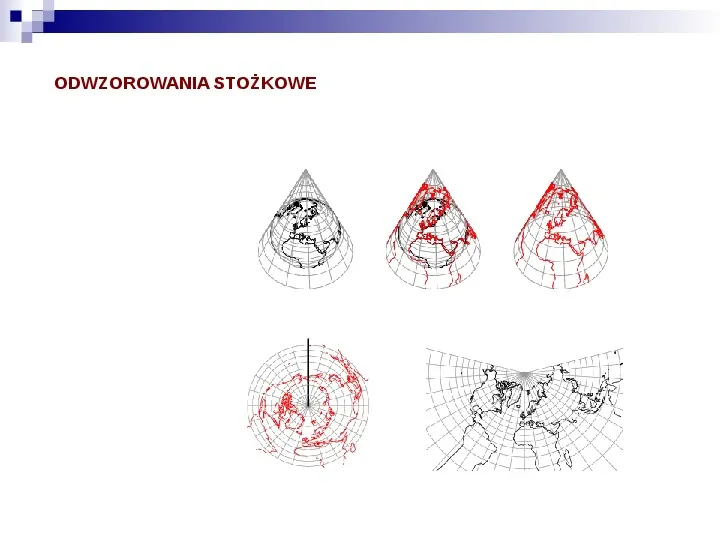
ODWZOROWANIA STOŻKOWE Odwzorowania stożkowe w aspekcie biegunowym posiadają cechy: południki są prostymi liniami, równoodległymi, zbieżnymi w punkcie, który może być biegunem, ale nie musi. W porównaniu do sfery, odległość kątowa między południkami jest zawsze zredukowana o stały czynnik, zwany czynnikiem stożkowym równoleżniki są łukami okręgów, koncentrycznych w punkcie zbieżności południków. W wyniku tego, równoleżniki przecinają wszystkie południki pod kątem prostym. Zniekształcenie jest stałe wzdłuż każdego równoleżnika. W celach zilustrowania, wynikowa płaszczyzna może zostać nawinięta na stożek z wierzchołkiem odwzorowywanej sfery, jednakże niewiele odwzorowań jest opartych na prawdziwej geometrycznej perspektywie (innymi słowy, stożek otrzymujemy zawsze w wyniku odwzorowania, jednakże rzadko bezpośrednio podczas tworzenia odwzorowania). Najczęściej stożek przecina sferę w jednym lub dwu wybranych równoleżnikach, zwanych standardowymi liniami. Prosta konstrukcja i wzorzec zniekształcenia, powoduje, że jego stosowanie w regionalnych i państwowych mapach stref umiarkowanych (podczas gdy mapy płaszczyznowe i walcowe są odpowiedniejsze dla stref biegunowych i tropikalnych), w szczególności dla obszarów ograniczonych dwoma położonymi niedaleko południkami, takimi jak Rosja lub USA. Z drugiej strony odwzorowania stożkowe rzadko nadają się dla map całego świata. Istnieje tylko jeden rodzaj odwzorowania stożkowego wiernopowierzchniowego, i tylko jedno jest wiernokątne. Ograniczenia są osłabione w odwzorowaniach pseudostożkowych (z zakrzywionymi południkami) oraz polistożkowych (z niekoncentrycznymi równoleżnikami ).

Slide 28

ODWZOROWANIA STOŻKOWE

Slide 29

ODWZOROWANIE LAMBERTA WIERNOKĄTNE STOŻKOWE Standardowy równoleżnik 50N and 10S, obciete przy 50S.

Slide 30

ODWZOROWANIE LAMBERTA WIERNOKĄTNE STOŻKOWE

Slide 31

WPROWADZENIE DO ALGORYTMÓW GIS GRUPA Grupą nazywamy parę (G,), gdzie G jest dowolnym zbiorem niepustym, a działaniem dwuargumentowym ( : G x G G) spełniającym następujące warunki: 1. dla dowolnych a, b, c należących do G zachodzi równość: (a b) c a (b c) (łączność działania) 2. istnieje w G taki element e, że dla każdego a należącego do G zachodzi równość: e a a e a (gdzie e nazywamy elementem neutralnym grupy) 3. dla każdego a należącego do G istnieje w G element a-1 taki, że: a a-1 a-1 a e (gdzie a-1 nazywamy elementem odwrotnym do a) GRUPA ABELOWA Jeżeli oprócz powyższych aksjomatów grupy, działanie w grupie G spełnia dodatkowo warunek przemienności: 4. dla dowolnych a, b w G zachodzi równość: a b b a, to grupę G nazywamy grupą przemienną lub grupą abelową.

Slide 32

PIERŚCIEŃ Pierścień (ang. ring) to struktura algebraiczna P z dwoma działaniami, zwanymi dodawaniem i mnożeniem, spełniającymi następujące aksjomaty: zbiór P z dodawaniem jest grupą abelową mnożenie jest łączne mnożenie jest obustronnie rozdzielne względem dodawania: a(b c) (ab) (ac) (b c)a (ba) (ca) CIAŁO Ciało (ang. field) to struktura algebraiczna K z dwoma działaniami, zwanymi dodawaniem i mnożeniem, spełniającymi następujące aksjomaty: zbiór K jest co najmniej dwuelementowy zbiór K z dodawaniem jest grupą abelową zbiór K - 0 z mnożeniem, gdzie Zero jest elementem neutralnym dodawania, jest grupą abelową mnożenie jest obustronnie rozdzielne względem dodawania: a(b c) (ab) (ac) (b c)a (ba) (ca)

Slide 33

POJĘCIE PRZESTRZENI WEKTOROWEJ (LINIOWEJ)

Slide 34

DEFINICJA PODRZESTRZENI WEKTOROWEJ Niepusty podzbiór S przestrzeni wektorowej V nazywamy podprzestrzenia wektorowa przestrzeni V , jezeli S z działaniami indukowanymi z V jest przestrzenia wektorowa. Podprzestrzenią liniową przestrzeni V nad ciałem K nazywamy taki jej podzbiór U, który sam jest przestrzenią liniową nad ciałem K ze względu na działania określone w V. PRZYKŁADY PODPRZESTRZENI WEKTOROWYCH Funkcje wielomianowe na R tworza podprzestrzen wektorowa przestrzeni wszystkich funkcji na R. Równiez przestrzen Wn wielomianów stopnia nie wkększego od n jest przestrzenia wektorowa, podprzestrzenia przestrzeni wszystkich wielomianów (funkcji wielomianowych). Inne podprzestrzenie przestrzeni Map(R,R): wielomianów parzystych, funkcji ciagłych, funkcji rózniczkowalnych, etc. Przykładami podprzestrzeni są: zbiór złożony z wektora zeroweg i cała przestrzeń. Nietrywialnym przykładem jest podzbiór przestrzeni euklidesowej R2 złożony z wszystkich wektorów postaci (x, 0).

Slide 35

BAZA I WSPÓŁRZĘDNE WEKTORA Baza przestrzeni liniowej to taki zbiór wektorów, że każdy wektor przestrzeni można zapisać jednoznacznie w postaci kombinacji liniowej wektorów bazy. Dla danej bazy i danego wektora współczynniki tej kombinacji liniowej, która przedstawia wektor nazywamy współrzędnymi wektora w bazie. Po wybraniu bazy każdy wektor jest jednoznacznie wyznaczony przez ciąg swych współrzędnych w tej bazie. Na przykład, w przestrzeni euklidesowej R2 bazę tworzy zbiór (1, 1), (0, 1). Wektor (3, 1) daje się zapisać jako (3, 1) 3(1, 1) 4(0, 1). Liczby 3 i 4 są współrzędnymi wektora (3, 1) w wybranej bazie. W innej bazie te same liczby będą współrzędnymi innego wektora. Każda przestrzeń liniowa ma bazę (fakt ten jest równoważny aksjomatowi wyboru); wszystkie bazy przestrzeni liniowej są równoliczne. WYMIAR PRZESTRZENI Moc dowolnej bazy przestrzeni V nazywamy wymiarem przestrzeni liniowej i oznaczamy symbolem dim(V). Przestrzeń, która ma bazę skończoną nazywamy skończenie wymiarową, w przeciwnym wypadku mówimy o przestrzeni nieskończenie wymiarowej.

Slide 36

DEFINICJA PRZESTRZENI EUKLIDESOWEJ Przestrzenią euklidesową n-wymiarową (n 1) nazywamy zbiór Rn wszystkich uporządkowanych układów (x1, x2, ..., xn) n liczb rzeczywistych, wraz z odległością dwóch układów określoną wzorem: d(x,y)sqrt(x1-y1)2(x2-y2)2dots(xn-yn)2 gdzie x (x1, x2, ..., xn) i y (y1, y2, ..., yn). Formalnie, Rn jest n krotnym iloczynem kartezjańskim zbioru liczb rzeczywistych przez siebie. Elementy x zbioru Rn nazywamy punktami, a liczby x1, x2, ..., xn, współrzędnymi punktu x. Wzór na odległość dwóch punktów jest uogólnieniem twierdzania Pitagorasa zapisanego we współrzędnych kartezjańskich dla n 2. Określoną tym wzorem odległość nazywamy odległością euklidesową.

Slide 37

PŁASZCZYZNA Wektorami są tu klasycznie pojmowane wektory na płaszczyźnie, a skalarami - liczby rzeczywiste. Bazę płaszczyzny tworzy dowolny zbiór złożony z dwu nierównoległych wektorów. Podobnie można pojmować każdą przestrzeń euklidesową (uwaga: mówienie, że płaszczyzna jest przestrzenią wektorową to nadużycie - staje się ona nią dopiero po wyposażeniu w strukturę dodawania wektorów i mnożenia ich przez skalary). Warto pamiętać, że wszystkie wektory płaszczyzny rozumianej jako przestrzeń wektorowa są zaczepione w początku układu współrzędnych. Aby dodawać wektory zaczepione w różnych punktach konieczne jest rozszerzenie przestrzeni wektorowej do przestrzeni afinicznej, w której wprowadzamy dodatkową operację przesunięcia równoległego. CIAŁO JAKO PRZESTRZEŃ LINIOWA Każde ciało można rozpatrywać jako przestrzeń liniową nad jego dowolnym podciałem. Na przykład, ciało liczb zespolonych jest przestrzenią liniową nad ciałem liczb rzeczywistych. Wymiar tej przestrzeni wynosi 2 jest ona izomorficzna z płaszczyzną euklidesową. Podobnie, ciało liczb rzeczywistych jest przestrzenią liniową nad ciałem liczb wymiernych. Jest to przestrzeń nieskończenie wymiarowa (wymiaru continuum). Dowolną bazę tej przestrzeni nazywamy bazą Hamela. .

Slide 38

PRZESTRZEŃ Kn Dla dowolnej liczby naturalnej n, rozważmy zbiór wszystkich uporządkowanych układów n skalarów z ciała K: Kn (k1, k2, ..., kn): ki należy do K dla i 1, 2, ..., n. Jeżeli określić dodawanie takich układów wzorem: (k1, k2, ..., kn) (l1, l2, ..., ln) (k1 l1, k2 l2, ..., kn ln) oraz mnożenie przez skalar α wzorem: α(k1, k2, ..., kn) (αk1, αk2, ..., αkn), to otrzymamy n-wymiarową przestrzeń liniową nad ciałem K. Jeżeli przyjąć tu K R, otrzymujemy n-wymiarową przestrzeń euklidesową PRZESTRZENIE FUNKCYJNE Wektorami są tu funkcje rzeczywiste (lub zespolone) określone na pewnym zbiorze X, zaś skalarami liczby rzeczywiste (zespolone w przypadku zespolonym). Dodawanie funkcji (wektorów) jest określone wzorem: (fg)(x) f(x) g(x), a mnożenie funkcji (wektora) przez liczbę wzorem: (αf)(x) αf(x) Na przykład, dodając funkcje f(x) 2x i g(x) x2 x otrzymamy funkcję y x2 x; mnożąc f przez 2 otrzymamy funkcję y 4x. Jeżeli zbiór X jest nieskończony, to tak otrzymana przestrzeń jest nieskończenie wymiarowa. Określając w zbiorze X dodatkowe struktury (np. przestrzeni topologicznej) otrzymujemy p. liniowe o specyficznych własnościach, które są przedmiotami badań odrębnych działów matematyki topologii, analizy matematycznej lub analizy funkcjonalnej.

Slide 39

Przestrzeń funkcji ograniczonych Niech X będzie dowolnym zbiorem. Zbiór B(X) wszystkich funkcji ograniczonych na X jest przestrzenią liniową. Przestrzeń funkcji ciągłych Niech X będzie przedziałem domkniętym. Zbiór C(X) wszystkich funkcji ciągłych na X jest p. liniową. Przestrzeń funkcji różniczkowalnych Niech X będzie przedziałem otwartym. Zbiór C(X) wszystkich funkcji różniczkowalncyh na X jest przestrzenią liniową. Przestrzeń ciągów bezwzględnie sumowalnych Niech X N rozważmy zbiór l1 wszystkich ciągów x(x1, x2, x3, ...) dla których szereg liczbowy xi jest zbieżny. Z nierówności trójkąta wynika, że suma dwóch ciągów o opisanej własności znów ma tę własność, a to oznacza, że otrzymana przestrzeń jest przestrzenią liniową. Przestrzeń ciągów sumowalnych z kwadratem Niech X N rozważmy zbiór l2 wszystkich ciągów x(x1, x2, x3, ...) dla których szereg liczbowy xi2 jest zbieżny. Z nierówności Schwarza wynika, że suma dwóch ciągów o opisanej własności znów ma opisaną własność, a to oznacza, że otrzymana przestrzeń jest przestrzenią liniową. Przestrzeń macierzy nad ciałem Zbiór wszystkich macierzy wymiaru nm nad danym ciałem tworzy przestrzeń liniową nad tym ciałem. Jej wymiar jest równy nm. Wielomiany Pierścień K[1] wielomianów o współczynnikach w ciele K jest przestrzenią liniową nad K. Jest to przestrzeń nieskończenie wymiarowa, jej bazą jest np. zbiór wielomianów 1, X, X2, X3,....

Slide 40

DEFINICJA ILOCZYNU SKALARNEGO Iloczyn skalarny wektorów to operacja (oznaczana symbolem lub ,), która każdej parze (x,y) wektorów z przestrzeni liniowej nad danym ciałem skalarów (najczęściej liczb rzeczywistych R lub zespolonych C) przypisuje skalar w taki sposób, że spełnione są poniższe warunki: PODSTAWOWE OKREŚLENIA W geometrii płaskiej klasyczna definicja iloczynu skalarnego związana jest z kątem między wektorami w przestrzeni: xy xy cos(x,y), gdzie x oznacza długość wektora x. Widać stąd, że jeżeli wektory x i y są prostopadłe to ich iloczyn skalarny jest równy 0. Zachodzi także zależność odwrotna: jeśli dwa niezerowe wektory mają zerowy iloczynskalarny to są prostopadłe. W ogólnym przypadku, jeśli xy0, to mówimy że wektory x i y są ortogonalne. NORMA GENEROWANA PRZEZ ILOCZYN SKALARNY Iloczyn skalarny pozwala określić (generować) normę wektora, czyli jego długość:x(xx).Ważną własnością tak otrzymanej normy jest tożsamość równoległoboku: 2x2 2y2 x y2 x - y2.

Slide 41

DEFNICJA PROSTYCH, REPREZENTACJA PROSTYCH Wyznaczanie odległości punktu od linii stanowi podstawową operację w grafice komputerowej, geometrii obliczeniowej oraz wszystkich dziedzinach wykorzystujących reprezentacje graficzne obiektów, tym w dziedzinie GIS. Powszechnie stosowane są podstawowe wzory na obliczanie odległości między punktami a innymi obiektami, w tym między liniami,. Jednakże bardzo często, konkretne rozwiązania wymagają stosowania tych a nie innych wzorów, co uzależnione jest rodzaju posiadanych danych i definicji problemu. W dalszych rozważaniach, konieczne będzie określenie metryki, czyli zdefiniowanie odległości między dwoma dowolnymi punktami badanej przestrzeni, w naszym przypadku przestrzeni Euklidesowej. Najczęściej do tego celu wykorzystywana jest standardowa Euklidesowa norma L2. W ten sposób, dla n-wymiarowego wektora v(v1,v2,...,vn), jego długość definiowana jest jako v: W przypadku dwu punktów P(p1,p2,...,pn) i Q(q1,q2,...,qn), odległość między tymi punktami wynosi:

Slide 42

REPREZENTACJE PROSTYCH Punktowa. Podstawowym sposobem zdefiniowania konkretnej linii L jest podanie dwu różnych punktów P0 i P1 leżących na tej linii. Linię L można również zdefiniować jako punkt z określonym kierunkiem. Niech L będzie punktem na linii a vL będzie niezerowym wektorem podającym kierunek linii. RÓWNANIE PROSTEJ Proste definiowane mogą być ponadto z wykorzystaniem współrzędnych punktów na linii jako niewiadomymi. Najczęściej spotykanymi reprezentacjami tego typu są podane w poniżej tabeli. Rodzaj Równanie Zastosowanie Jawna 2D y f(x) mx b Linie nie prostopadłe do osi Niejawna 2D f(x,y) ax by c 0 Dowolna linia 2D Parametryc zna P(t) P0 t vL Dowolna linia w n- wymiarowej przestrzeni.

Slide 47

POSTAĆ PARAMETRYCZNA PROSTEJ W celu obliczenia odległości d(P,L) (w dowolnej n-wymiarowej przestrzeni) od dowolnego zdefiniowanego punktu P do prostej L przedstawionej równaniem parametrycznym wykonywane zostają następujące operacje. Niech P(b) będzie punktem przecięcia prostopadłej z punktu P poprowadzonej do prostej L. Parametryczne równanie prostej dane jest w postaci: P(t)P0 t (P1P0). W takim przypadku, wektor P0P(b) przedstawia rzut wektora P0P na odcinek P0P1, sytuacja przedstawiona na poniższym rysunku: Przy vL(P1P0) i w(PP0), otrzymujemy: w ten sposób: przy uL będącym kierunkowym wektorem jednostkowym wektora L. Zaletą metod jest możliwość zastosowania dla przestrzeni dowolnego wymiaru n.

Slide 48

OPERACJE UPRASZCZANIA GENERALIZACJI DANYCH Transformacja atrybutów - klasyfikacja Selekcja tematyczna wybranie podzbioru atrybutów (klas) , które są istotne dla danego zastosowania (problemu) Agregacja tematyczna zmiana rozdzielczości tematycznej łączenie hierarchii klas Transformacja przestrzenna a) Poszczególne obiekty I) Upraszczanie symplifikacja: A1) przesiewanie linia zostaje reprezentowana poprzez podzbiór punktów linii wejściowej A2) swobodne upraszczanie reprezentacja linii poprzez dowolne punkty, a nawet poprzez ich większą liczbę II) zapadanie zmiana wymiarowości danych III) wzmocnienie Geometryczne ograniczenia A1) Powiększenie rozmiaru stałe skalowanie we wszystkich kierunkach A2) Nieproporcjonalne powiększenie odnosi się tylko do pewnych fragmentów prowadzi do zmiany kształtu Ograniczenia znaczeniowe A3) Wygładzanie lepszy wizualnie efekt A4) Fraktalizacja A5) Rektyfikacja nadanie kształtu prostokątów kwadratów

Slide 49

OPERACJE UPRASZCZANIA GENERALIZACJI DANYCH b) poszczególne obiekty lub zbiór obiektów IV) selekcja eliminacja A6) selekcja wybór najbardziej ważnych obiektów reprezentujących cechy właściwości obiektów poddawanych operacji upraszczania A7) eliminacja usuwanie obiektów, które nie są ważne V) przemieszczenie obiektów, które znajdują się zbyt blisko siebie VI) agregacja A1) dodanie atrybutów do jednego obiektu a1) amalgamacja fuzja (agregacja dwu sąsiadujących obiektów tego samego typu), scalanie (dwa obiekty nie sąsiadujące z sobą) a2) połączenie zbioru obiektów do jednego obiektu o większym wymiarze A2) dołączenie atrybutów kilku obiektów Typowanie transformacja zbioru obiektów na inny zbiór obiektów

Slide 50

UPRASZCZANIE OBIEKTÓW LINIOWYCH W szeregu zastosowaniach, podczas przetwarzania danych, w tym danych geograficznych, poszczególne składowe obiektów, znajdują się w bezpośredniej bliskości. Podczas operacji odrysowywania takich obiektów, składowe tych obiektów redukują się do pojedynczych punktów. Względy wydajności i efektywności przetwarzania danych wymagają doprowadzania do sytuacji, w której zdegenerowane do punktu linie nie są odrysowywane. W tym celu konieczne jest zredukowanie liczby wierzchołków i krawędzi obiektów linii do jedynie tych istotnych i zapewniających odpowiednią rozdzielczość w ramach konkretnego zastosowania. Opracowano kilka algorytmów mających na celu aproksymowanie obiektu linii o dużej rozdzielczości (liczbie wierzchołków) mniejszą ich liczbą. Zastosowanie algorytmu redukcji liczby wierzchołków wpływa ponadto także na szybkość działania pozostałych algorytmów, takich jak na przykład wypełnianie powierzchni lub określanie przecięć, które mają zostać wykorzystane do obiektów linii i poligonów

Slide 51

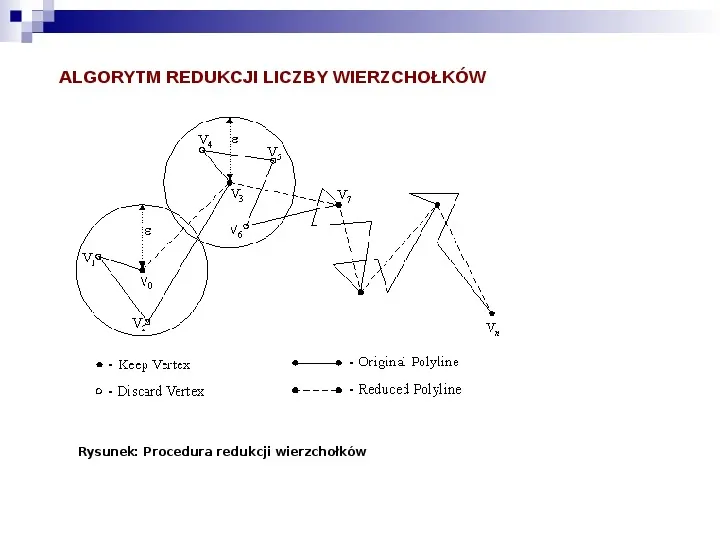
ALGORYTM REDUKCJI LICZBY WIERZCHOŁKÓW I ALGORYTM DOUGLAS-PEUCKER Pierwszym algorytmem, najprostszym i zarazem najczęściej wykorzystywanym do zmniejszania liczby punktów prostych jest szybki algorytm redukcji wierzołków o złożoności O(n). Algorytm jest najszybszym oraz zarazem najmniej skomplikowanym algorytmem z dostępnych algorytmów jednak z stosunkowo małą dokładnością wyników. Z tego względu algorytm redukcji wierzchołków zostaje połączony z bardziej dokładnymi algorytmami upraszczania, które za dane wejściowe pobierają zredukowane w ten sposób obiekty i dalej przetwarzają te dane w sposób wolniejszy, jednak zarazem bardziej dokładnie. Najbardziej znanym algorytmem upraszczania obiektów liniowych jest klasyczny algorytm Douglasa Peuckera (DP) aproksymacji obiektów liniowych wykorzystywany szeroko w grafice komputerowej oraz systemach GIS. Istnieją dwa warianty algorytmu DP, oryginalna metoda O(n2) [Douglas Peucker, 1973] oraz nowsza wersja O(n log n) one [Hershberger Snoeyink, 1992]. Metoda druga, pomimo oferowania zysku czasowego, wiąże się ze skomplikowaną implementacją oraz ograniczeniem zastosowania jedynie do obiektów dwuwymiarowych.

Slide 52

ALGORYTM REDUKCJI LICZBY WIERZCHOŁKÓW Rysunek: Procedura redukcji wierzchołków

Slide 53

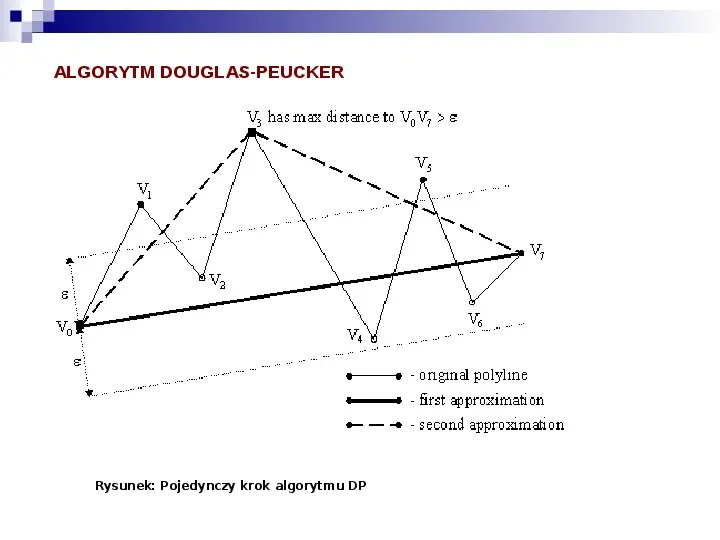
ALGORYTM DOUGLAS-PEUCKER Rysunek: Pojedynczy krok algorytmu DP

Slide 54

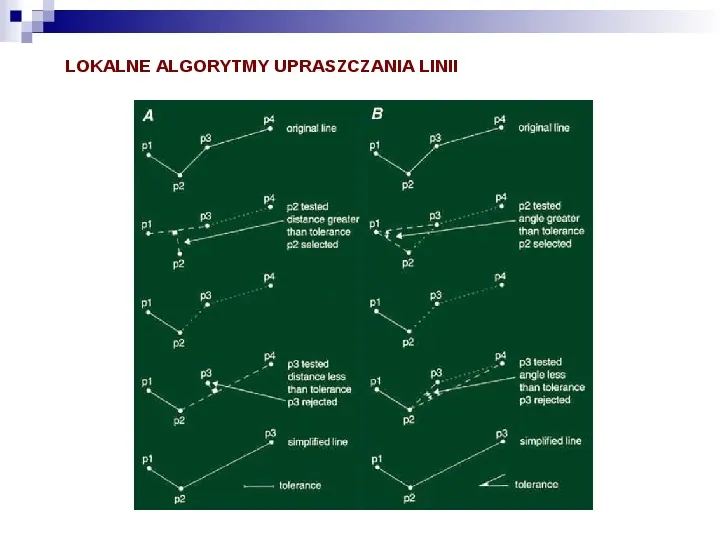
LOKALNE ALGORYTMY UPRASZCZANIA LINII

Slide 55

POJĘCIE APROKSYMACJI Aproksymacja jest to przybliżanie, zastępowanie jednych wielkości drugimi. Aproksymacja może dotyczyć dowolnych wielkości matematycznych liczb, funkcji, krzywych, obszarów, wektorów, macierzy. Zastępowanie danej wielkości inną obarczone jest pewnym błędem. Oszacowanie wielkości błędu pozwala na ocenę, czy dane przybliżenie jest zadawalające, czy też nie. Niech poszukiwana jest krzywa y F (x ) dla zadanej liczby punktów: jest opisana równaniem: ( xi , yi ) F ( x) c1 f1 ( x) c2 f 2 ( x) ... cn f n ( x) Aproksymacja stosowana jest wówczas, gdy ilość zadanych punktów m jest mniejsza od ilości nieznanych współczynników n krzywej F(x). Zwykle nie można przeprowadzić krzywej przez wszystkie punkty. Poszukiwana jest wówczas najbliższa krzywa w sensie minimum kwadratu błędu.

Slide 56

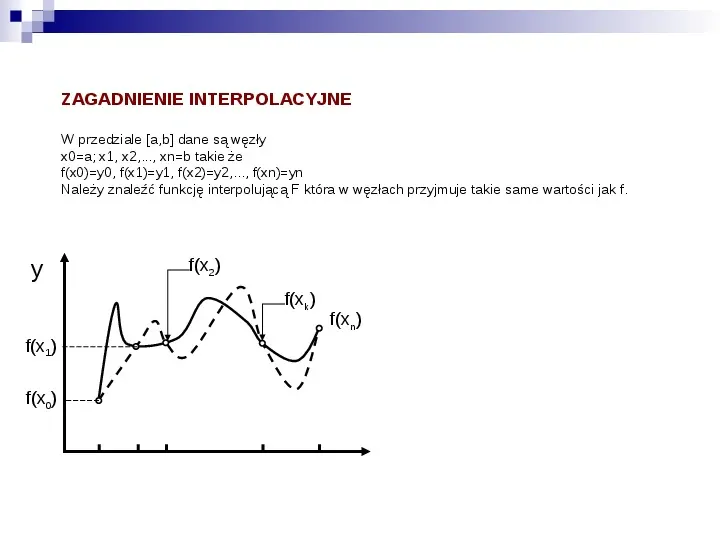
ZAGADNIENIE INTERPOLACYJNE W przedziale [a,b] dane są węzły x0a; x1, x2,..., xnb takie że f(x0)y0, f(x1)y1, f(x2)y2,..., f(xn)yn Należy znaleźć funkcję interpolującą F która w węzłach przyjmuje takie same wartości jak f. y f(x2) f(xk) f(x1) f(x0) f(xn)

Slide 57

Cel interpolacji Znalezienie funkcji odpowiedniej klasy przechodzącej przez dany zestaw punktów (węzłów) w przestrzeni dwu- lub więcej wymiarowej. Rodzaje interpolacji: Interpolacja wielomianami Interpolacja funkcjami wymiernymi Interpolacja funkcjami trygonometrycznymi Interpolacja funkcjami sklejanymi Zastosowanie interpolacji: Szacowanie określonych wielkości w punktach pośrednich. Prowadzenie gładkich krzywych lub powierzchni przez punkty pomiarowe lub z symulacji (funkcje sklejane). Algorytmy numeryczne, np.: Znajdowanie miejsc zerowych funkcji Uzbieżnianie procesów iteracyjnych (np. SCF) Różniczkowanie i całkowanie numeryczne.

Slide 58

WZÓR INTERPOLACJNY LAGRANGEA n Wn x a o a 1x a 2 x ... a n x a k x 2 n k 0 2 o n o 2 1 n 1 a o a 1x o a 2 x ... a n x y o a o a 1x1 a 2 x ... a n x y1 .................................................. 2 n n n a o a 1x n a 2 x ... a n x y n k

Slide 59

WZÓR INTERPOLACJNY LAGRANGEA ak 1 xo 1 x1 ... ... 1 x k 1 det 1 xk 1 x k 1 ... ... 1 x n x o2 x12 ... x 2k 1 x 2k x 2k 1 ... x 2n ... ... ... ... ... ... ... ... 1 xo 1 x1 det .. ... 1 x n x ok 1 x1k 1 ... x kk 11 x kk 1 x kk 11 ... x kn 1 yo y1 ... yk 1 yk y k 1 ... yn ... x on n ... x1 ... ... ... x nn ... x on n ... x1 ... ... ... x nk 1 ... x nk ... x nk 1 ... ... ... x nn

Slide 60

WZÓR INTERPOLACJNY LAGRANGEA Wn x yo Lo x y1 L1 x ... yn Ln x Lk(x) jest wielomianem stopnia co najwyżej n Wn xk yo Lo xk y1 L1 xk ... yn Ln xk yk 0 gdy j k L j xk 1 gdy j k Zatem L j x x x xo x x1 ... x j x j 1 x x j 1 ... x xn xo x j x1 ... x j x j 1 x j x j 1 ... x j xn

Slide 61

WZÓR INTERPOLACYJNY NEWTONA ILORAZY RÓŻNICOWE f ( x1 ) f ( x o ) f ( x o ; x1 ) x1 x o f ( x1 ; x 2 ) f ( x o ; x1 ) f ( x o ; x1 ; x 2 ) x2 xo ...................................................... f ( x1 ; x 2 ; x 3 ; x n ) f ( x o ; x1 ; x 2 ;...; x n 1 ) f ( x o ; x1 ; x 2 ;...; x n ) xn xo

Slide 62

SCHEMAT OBLICZANIA ILORAZÓW RÓŻNICOWYCH xo f ( xo ) f ( xo ; x1 ) x1 f ( x1 ) f ( xo ; x1 ; x2 ) f ( x1 ; x2 ) x2 f ( x2 ) f ( xo ; x1 ; x2 ; x3 ) f ( x1 ; x2 ; x3 ) f ( x2 ; x3 ) x3 f ( x3 ) f ( x2 ; x3 ; x4 ) f ( x4 ) x5 f ( x5 ) f ( x1 ; x2 ; x3 ; x4 ; x5 ) f ( x2 ; x3 ; x4 ; x5 ) f ( x3 ; x4 ; x5 ) f ( x4 ; x5 ) f ( xo ; x1 ; x2 ; x3 ; x4 ; x5 ) f ( x1 ; x2 ; x3 ; x4 ) f ( x3 ; x4 ) x4 f ( xo ; x1 ; x2 ; x3 ; x4 )

Slide 63

SCHEMAT OBLICZANIA ILORAZÓW RÓŻNICOWYCH n f (x j ) j0 ( x j x o )( x j x1 )...( x j x j 1 )( x j x j1 ) ( x j x n ) f ( x o ; x1 ;...; x n ) W n ( x ) f ( x o ) f ( x o ; x1 )o ( x ) f ( x o ; x1 ; x 2 )2 ( x ) ... f ( x o ; x1 ; x 2 ;...; x n )n 1 ( x ) k ( x ) ( x x o )( x x1 )...( x x k )

Slide 64

INTERPOLACJA WIELOMIANAMI HERMITEA Podobnie jak w przypadku wielomianów Lagrangea mamy n1 różnych wartości x0. x1,...,xn zmiennej niezależnej x oraz n1wartości funkcji y0. y1,...,yn . Dodatkowo musimy znać wartości pochodnych w punktach interpolacji do rzędu m. Na tych punktach interpolacji budujemy wielomian Hermitea, który jest wielomianem potęgowym stopnia (m1)(n1)-1 spełniającym warunki dk H i j ( xl ) ik jl k dx rząd pochodnej i, k 0,1, , m j , l 0,1 , n nr punktu przedziału dla którego wielomian przyjmuje wartość 1

Slide 65

INTERPOLACJA WIELOMIANAMI HERMITEA W przypadku m 0 wielomian Hermitea jest wielomianem Lagrangea Wprowadzamy następującą jednoindeksową numerację wielomianów Hermitea. Hi(m1) j (x) Hij(x) p i(m1)j Hp(x) Hij(x) i 0,1,...,m j 0,1,...,n

Slide 66

INTERPOLACJA WIELOMIANAMI HERMITEA Niech apq oznacza współczynniki rozwinięcia p-tego wielomianu Hermitea, to wielomian Hermitea można zapisać w postaci ( m 1)( n 1) 1 q 2 ( m 1 )( n 1) 1 a x a 1 a x a x a x pq p0 p1 p2 p ,( m 1)( n 1) 1 H p ( x) q 0 Czyli mając dane x0 , wprowadzany oznaczenia x1 , x n x0 , x1 , xn y 0 , y1 , y n y00 , y01 , y0 n y 0 , y1 , y n y10 , y11 , y1n ym 0 , ym1 , ymn y 0( m ) , y1( m ) , y n( m )

Slide 67

INTERPOLACJA WIELOMIANAMI HERMITEA m n y ( x) yij H ij ( x) i 0 j 0 Wielomian Hermitea Najczęściej wielomiany Hermitea stosujemy dla dwóch punktów x0, x1 przy znanych wartościach y0, y1 oraz znanych pierwszych pochodnych y0, y1 czyli n1, m1, (m1)(n1)-13 Wtedy wielomian Hermitea przyjmie postać 3 H p ( x) H ij ( x) a pq x q q 0

Slide 68

Wielomian Hermitea dla punktu x1 3 H1 ( x1 ) H 01 ( x1 ) a1q x1q q 0 a10 1 a11 x1 a12 x12 a13 x13 1 a10 x1 a11 x12 a12 x13 a13 1 x1 x12 a10 a x13 11 a12 a13

Slide 69

Wielomian Hermitea dla pierwszej pochodnej w punkcie x0 3 H 2 ( x 0 ) H 10 ( x0 ) a 2 q qx0q 1 q 0 a 20 0 a 21 1 a 22 2 x 0 a 23 3 x 02 0 a 20 1 a 21 2 x 0 a 22 3 x 02 a 23 0 1 2 x0 a 20 a 3 x 02 21 a 22 a 23

Slide 70

Wielomian Hermitea dla pierwszej pochodnej w punkcie x1 3 H 3 ( x1 ) H11 ( x1 ) a3q qx1q 1 q 0 a30 0 a31 1 a32 2 x1 a33 3 x12 0 a30 1 a31 2 x1 a32 3 x12 a33 0 1 2 x1 a30 a 3 x12 31 a32 a33

Slide 71

Łącząc te macierze w jedną macierz otrzymujemy grupę układów równań liniowych CAI 1 x 0 1 x1 0 1 0 1 x02 x12 2 x0 2 x1 x 03 a 00 x13 a 01 3x 02 a 02 2 3x1 a 03 C a10 a11 a 20 a 21 a12 a 22 a13 a 23 A a30 1 a31 0 a32 0 a33 0 0 0 0 1 0 0 0 1 0 0 0 1 I Rozwiązując powyższą grupę układów równań liniowych otrzymujemy komplet współczynników w postaci macierzy A C-1 , gdzie C jest kwadratową macierzą o wymiarach (n1)(m1) (n1)(m1) której wyrazy określone są zależnością C i ( m 1) j ,q dj q j xi dx

Slide 72

REPREZENTACJA KRZYWYCH W PRZESTRZENI

Slide 73

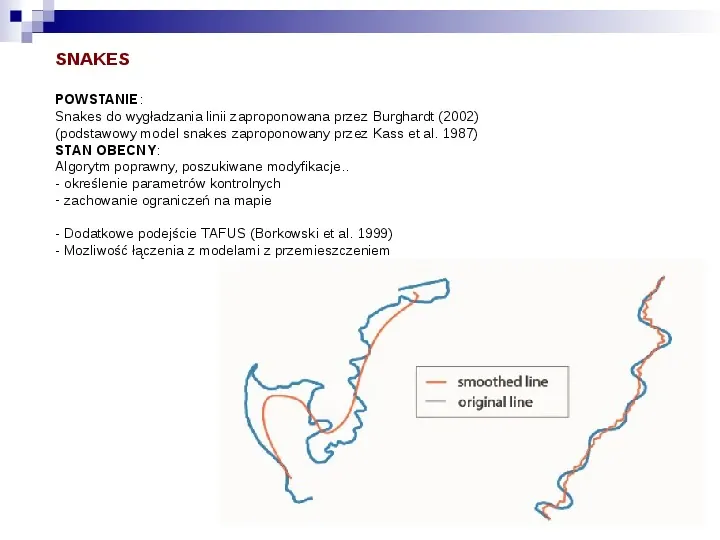
SNAKES POWSTANIE: Snakes do wygładzania linii zaproponowana przez Burghardt (2002) (podstawowy model snakes zaproponowany przez Kass et al. 1987) STAN OBECNY: Algorytm poprawny, poszukiwane modyfikacje.. - określenie parametrów kontrolnych - zachowanie ograniczeń na mapie - Dodatkowe podejście TAFUS (Borkowski et al. 1999) - Mozliwość łączenia z modelami z przemieszczeniem

Slide 74

ZASADA DZIAŁANIA Snakes funkcja minimalizująca energię stosowana w grafice do rozpoznawania obrazów wygładza sygnały (linie) jak krzywa sklajana specyficznie, wygładzanie kontrolowane jest lokalnie całka snakes zdefiniowana przez dwie wielkości internal energy : energię wewnętrzną opisującą sam kształt linii external energy : energia zewnętrzna opisująca zewnętrzne siły łaczna energia ma być minimalizowana rozwiazanie iteracyne

Slide 75

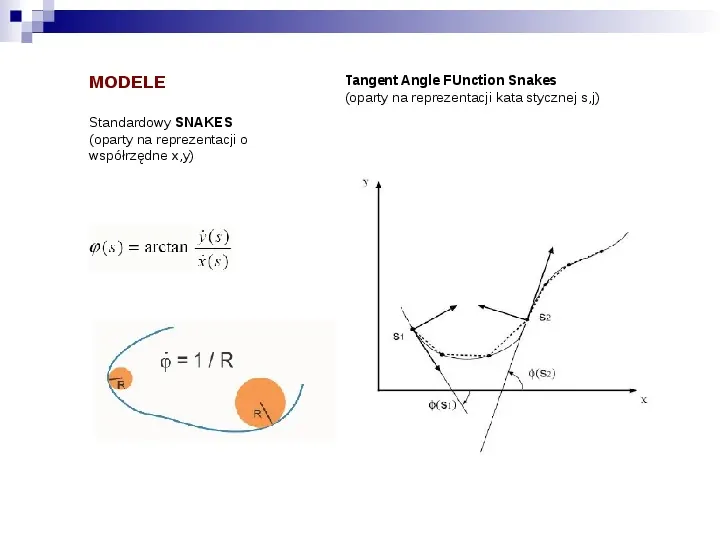
MODELE Standardowy SNAKES (oparty na reprezentacji o współrzędne x,y) Tangent Angle FUnction Snakes (oparty na reprezentacji kata stycznej s,j)

Slide 76

WYGŁADZANIE LINII Z WYKORZYSTANIEM ALGRYTMU SNAKES a,b : parametry kontrolne (1 pierwszy) j : kąt stycznej kropki : różniczka cząstkowa względem długości łuku s

Slide 78

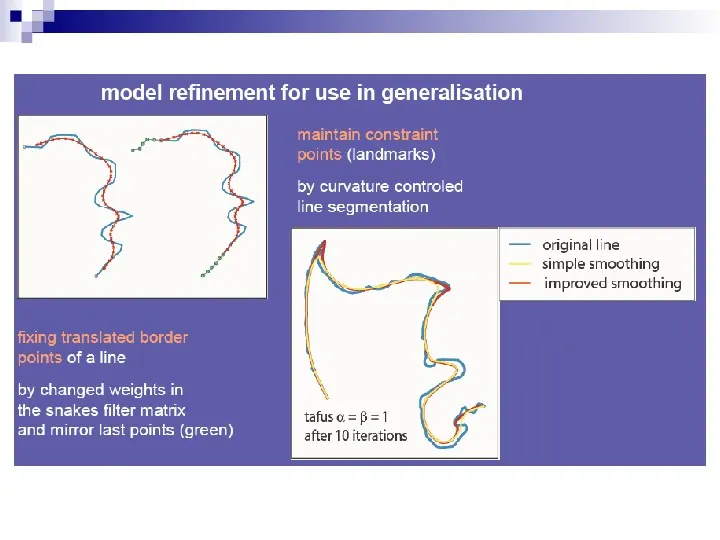
ENERGIA WENĘTRZNA I ZEWNĘTRZNA DLA ALGORYTMU SNAKES

Slide 79

WZORY POCHODNYCH ENERGII SNAKES

Slide 80

PODSTAWOWE WZORY DO OBLICZEŃ ENERGII DLA ALGORYTMU SNAKES

Slide 81

LITERATURA Snakes: a technique for line smoothing and displacement in map generalisation Stefan Steiniger (Zürich) Siegfried Meier (Dresden) Definicje serwis: http:www.zgapa.plzgapedia