Wzory skróconego mnożenia

Zobacz slidy

Treść prezentacji

Slide 1

Wzory skróconego mnożenia Prezentacja z matematyki Cezary Król kl. 2 H Gimnazjum nr 2 w Mielcu Głosu udzieliła Wioletta Król Luty 2006 Copyright 2006 by Czarek

Slide 2

Aby oglądać prezentację należy mieć włączone głośniki 2 2 ) b (a b a 2 a (a b) 2 WEJŚCIE a2- 2ab b2 2 ba2 b2 (a b) (a b) Copyright 2006 by Czarek

Slide 3

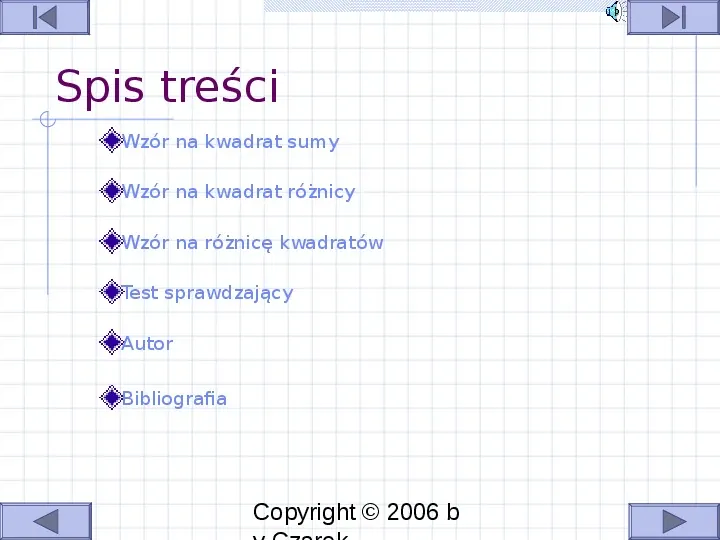
Spis treści Wzór na kwadrat sumy Wzór na kwadrat różnicy Wzór na różnicę kwadratów Test sprawdzający Autor Bibliografia Copyright 2006 b

Slide 4

Wzór na kwadrat sumy Aby oglądnąć filmik należy kliknąć na pole obok Copyright 2006 b

Slide 5

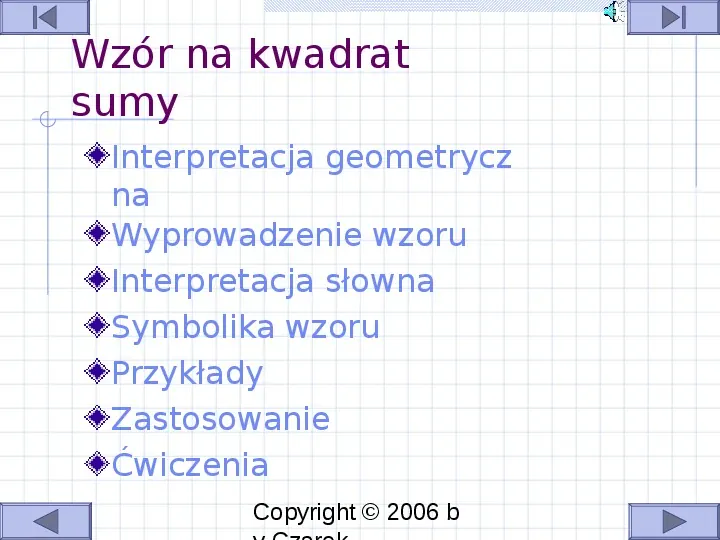
Wzór na kwadrat sumy Interpretacja geometrycz na Wyprowadzenie wzoru Interpretacja słowna Symbolika wzoru Przykłady Zastosowanie Ćwiczenia Copyright 2006 b

Slide 6

Interpretacja geometryczna Rysunek przedstawia kwadrat o boku ab. Pole tego kwadratu jest równe(ab)2 i jest sumą pól czterech figur. a (ab) b ab a b2 ab b 2 a Copyright (ab) 2006 b (ab)(ab) a2 2ab b2

Slide 7

Wyprowadzanie wzoru na podstawie definicji potęgi a2aa (a b)2 wykonujemy mnożenie sum algebraicznych (a b)(a b) redukujemy wyrazy podobne a2 ab ab b2 otrzymujemy gotowy wzór a 2ab b 2 2 Copyright 2006 b

Slide 8

Interpretacja słowna aib Kwadrat sumy dwóch jest równy sumie ich kwadratów powiększowyrażeń nej o podwojony iloczyn tych wyrażeń (a b) a2 2ab b2 2 Copyright 2006 b

Slide 9

Symbolika wzoru Kwadrat sumy - przekształca iloczyn postaci (ab)(ab) i pozwala na szybkie wykonanie obliczeń. (a b) a 2ab b 2 2 2 lub w postaci symbolicznej (a b )2 a 2 2 a b Copyright 2006 b b2

Slide 10

Przykłady (3a 2b)2 (3a)2 23a2b (2b)2 9a2 12ab 4b2 (4x 5y)2 (4x)2 24x5y (5y)2 16x2 40xy 25y2 Copyright 2006 b

Slide 11

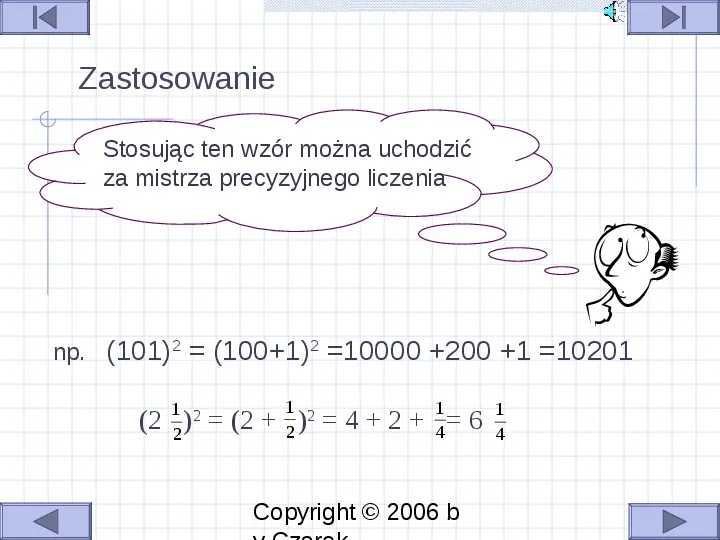
Zastosowanie Stosując ten wzór można uchodzić za mistrza precyzyjnego liczenia np. (101)2 (1001)2 10000 200 1 10201 (2 1 2 ) 2 (2 1 2 2) 42 1 4 Copyright 2006 b 6 1 4

Slide 12

Ćwiczenie 1 Podane wyrażenie (4x5y)2 przedstawione w postaci sumy ma postać: 16x2 40xy 25y2 4x2 40xy 5y2 16x2 20xy 25y2 Copyright 2006 b

Slide 13

NIESTETY ZŁA ODPOWIEDZ SPRÓBUJ JESZCZE RAZ Copyright 2006 b

Slide 14

PRAWIDŁOWA ODPOWIEDŹ!!! GRATULUJE Copyright 2006 b

Slide 15

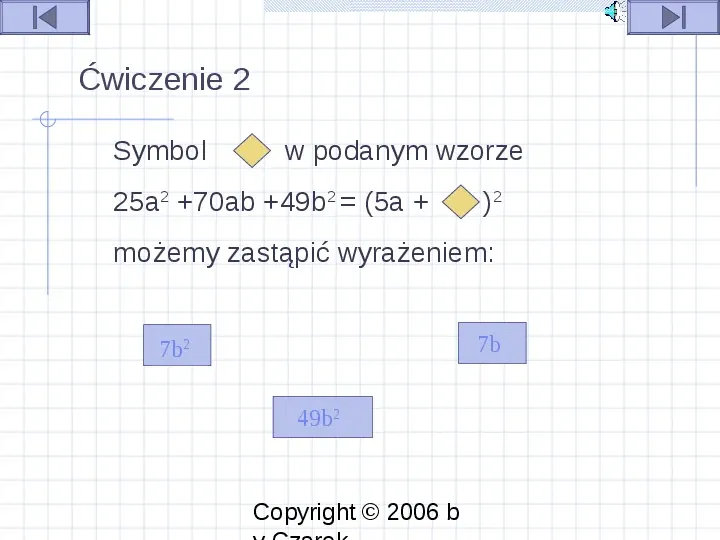
Ćwiczenie 2 Symbol w podanym wzorze 25a2 70ab 49b2 (5a )2 możemy zastąpić wyrażeniem: 7b 7b2 49b2 Copyright 2006 b

Slide 16

NIESTETY ZŁA ODPOWIEDZ SPRÓBUJ JESZCZE RAZ Copyright 2006 b

Slide 17

PRAWIDŁOWA ODPOWIEDŹ!!! GRATULUJE Copyright 2006 b

Slide 18

Wzór na kwadrat różnicy Aby oglądnąć filmik należy kliknąć na pole obok Copyright 2006 b

Slide 19

Wzór na kwadrat różnicy Interpretacja geometrycz na Wyprowadzenie wzoru Interpretacja słowna Symbolika wzoru Przykłady Ćwiczenia Copyright 2006 b

Slide 20

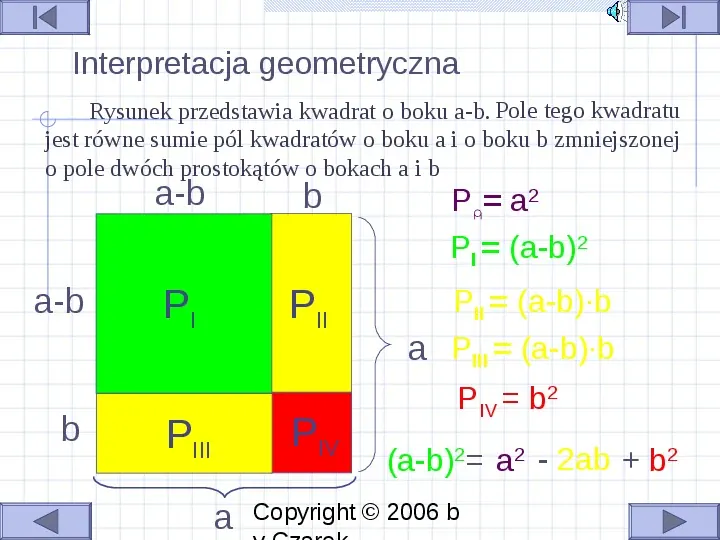
Interpretacja geometryczna Rysunek przedstawia kwadrat o boku a-b. Pole tego kwadratu jest równe sumie pól kwadratów o boku a i o boku b zmniejszonej o pole dwóch prostokątów o bokach a i b a-b b a-b b P a2 PI (a-b)2 PI PII PII (a-b)b a PIII (a-b)b PIV PIII a PIV b2 (a-b)2 a2 - 2ab b2 Copyright 2006 b

Slide 21

Wyprowadzanie wzoru (a - b)2 wykonujemy mnożenie sum algebraicznych (a - b)(a - b) redukujemy wyrazy podobne a2 - ab - ab - b2 otrzymujemy gotowy wzór a - 2ab b 2 2 Copyright 2006 b

Slide 22

Interpretacja słowna Kwadrat różnicy dwóch wyrażeń a i b jest równy sumie ich kwadratów pomniejszonej o podwojony iloczyn tych wyrażeń (a - b)2 a2 - 2ab b2 Copyright 2006 b

Slide 23

Symbolika wzoru Kwadrat różnicy - przekształca iloczyn postaci (a-b)(a-b) i pozwala na szybkie wykonanie obliczeń. (a - b) a - 2ab b 2 2 2 lub w postaci symbolicznej (a - ) b 2 2 a -2 2 b b a Copyright 2006 b

Slide 24

Przykłady (4b - 3)2 (4b)2 - 24b3 32 16b2 - 246 9 (6x 3z)2 (6x)2 - 26x3z (3z)2 36x2 - 36xz 9z2 Copyright 2006 b

Slide 25

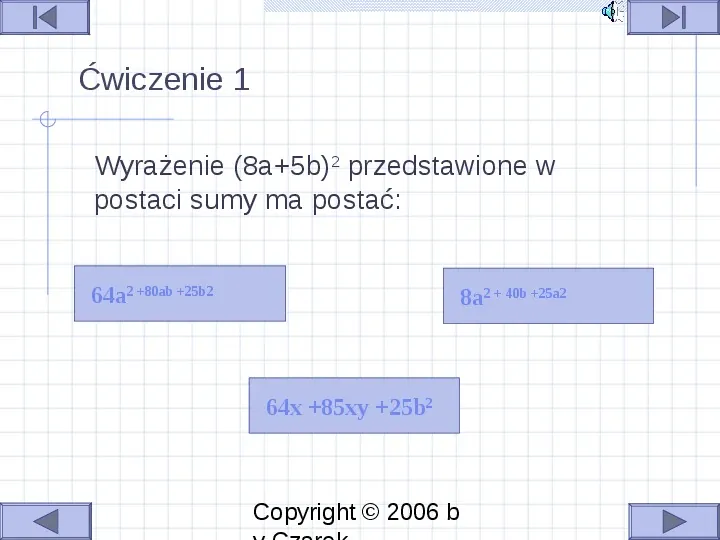
Ćwiczenie 1 Wyrażenie (8a5b)2 przedstawione w postaci sumy ma postać: 64a2 80ab 25b2 8a2 40b 25a2 64x 85xy 25b2 Copyright 2006 b

Slide 26

NIESTETY ZŁA ODPOWIEDZ SPRÓBUJ JESZCZE RAZ Copyright 2006 b

Slide 27

PRAWIDŁOWA ODPOWIEDŹ!!! GRATULUJE Copyright 2006 b

Slide 28

Ćwiczenie 2 Podaj wyrażenie 400 120 9 w postaci różnicy: (20 3)2 (20 3)2 (30 - 2)2 Copyright 2006 b

Slide 29

PRAWIDŁOWA ODPOWIEDŹ!!! GRATULUJE Copyright 2006 b

Slide 30

Wzór na różnicę kwadratów Aby oglądnąć filmik należy kliknąć na pole obok Copyright 2006 b

Slide 31

Wzór na różnicę kwadratów Interpretacja geometrycz na Dowód Interpretacja słowna Przykłady Ćwiczenia Copyright 2006 b

Slide 32

Interpretacja geometryczna Różnica pól kwadratów o bokach a i b jest równa polu prostokąta o bokach a b i a b a b a-b b a a-b a b a-b b a a b 2 2 (a b) (a b) Copyright 2006 b

Slide 33

Dowód a b (a b)(a b) 2 2 (a - b)(a b) a(ab) - b(ab) a2 ab - ba - b2 a2 b2 Copyright 2006 b

Slide 34

Interpretacja słowna Iloczyn sumy dwóch wyrażeń a i b przez ich różnicę jest równy różnicy kwadratów tych wyrażeń a2 b2 (a b) (a b) Copyright 2006 b

Slide 35

Przykłady 62 32 (6 3) (6 3) 3 9 202 42 (20 4) (20 4) 16 24 Copyright 2006 b

Slide 36

Ćwiczenie 1 Wyrażenie 102 - 42 przedstawione jako iloczyn ma postać: (10 4) (10 4) (10 4) (10 4) (10 4) (10 4) Copyright 2006 b

Slide 37

NIESTETY ZŁA ODPOWIEDZ SPRÓBUJ JESZCZE RAZ Copyright 2006 b

Slide 38

PRAWIDŁOWA ODPOWIEDŹ!!! GRATULUJE Copyright 2006 b

Slide 39

Ćwiczenie 2 Co powinno znajdować się w miejscu kropek (34f ...) (34f 6g) : 6k 34f 6g Copyright 2006 b

Slide 40

NIESTETY ZŁA ODPOWIEDZ SPRÓBUJ JESZCZE RAZ Copyright 2006 b

Slide 41

PRAWIDŁOWA ODPOWIEDŹ!!! GRATULUJE Copyright 2006 b

Slide 42

Test sprawdzający Aby oglądnąć filmik należy kliknąć na pole obok Copyright 2006 b

Slide 43

UWAGA! Aby rozwiązać test, należy oglądnąć całą prezentację POCZĄT EK TEST Copyright 2006 b

Slide 44

Test sprawdzający W podanym wyrażeniu 202 2 20 1 12 użyto wzoru na: a) kwadrat sumy b) kwadrat różnicy c) różnicę kwadratów Copyright 2006 b

Slide 45

NIESTETY ZŁA ODPOWIEDZ SPRÓBUJ JESZCZE RAZ Copyright 2006 b

Slide 46

PRAWIDŁOWA ODPOWIEDŹ!!! GRATULUJE Copyright 2006 b

Slide 47

Znajdź wyrażenie w którym użyto wzór na kwadrat sumy: a) 9a2 36ab 4b2 b) 9k2 - 36kl 4l2 c) (10z 6y) (10z 6y) Copyright 2006 b

Slide 48

NIESTETY ZŁA ODPOWIEDZ SPRÓBUJ JESZCZE RAZ Copyright 2006 b

Slide 49

PRAWIDŁOWA ODPOWIEDŹ!!! GRATULUJE Copyright 2006 b

Slide 50

Autor Bibliografia Koniec Pokazu Copyright 2006 b

Slide 51

Autor Cezary Król kl.2 H Rok szk. 200506 Gimnazjum nr 2 w Mielcu krolewicz1o2.pl Copyright 2006 b

Slide 52

Bibliografia Matematyka Podręcznik dla 2 klasy gimnazjum Maciej Bryński i Janusz Kaja wydawnictwo Juka Matematyka Zbiór zadań dla 2 klasy gimnazjum Norbert Dróbka i Karol Szymański wydawnictwo Juka Zeszyt przedmiotowy z matematyki kl.2 Copyright 2006 b

Slide 53

Dziękuję za uwagę KONIEC Copyright 2006 b