Pola figur płaskich

Zobacz slidy

Treść prezentacji

Slide 1

ANNA BERLIŃSKA KOMZA GIMNAZJUM NR 1 W SIERADZU

Slide 2

Pole jest liczbą, która wyraża ilość kwadratów jednostkowych mieszczących się w obszarze danej figury. Pole tej figury jest równe 12, gdyż w obszarze tej figury mieści się dwanaście jednakowych kwadratów.

Slide 3

Kwadrat o boku 1 mm i polu równym 1 mm 2 2 Kwadrat o boku 1 cm i polu równym 1 cm Kwadrat o boku 1 dm i polu równym 1 dm itd. 2

Slide 4

To jest 1 cm 2. To jest 1 dm 2. Czy wiesz, że w jednym decymetrze kwadratowym mieści się sto centymetrów kwadratowych! 2 1 dm 100 cm 2

Slide 5

Jednostki kwadratowe służą do wyrażania pola (powierzchni) danej figury. Podstawowe jednostki kwadratowe, to: jeden milimetr kwadratowy 1mm 2 jeden centymetr kwadratowy 1cm 2 jeden decymetr kwadratowy 1 dm 2 jeden metr kwadratowy 1m 2 jeden kilometr kwadratowy 1 km 2

Slide 6

Jeden ar (1a), to pole kwadratu o boku 10 m. 1 a 100 m 2 Jeden hektar (1ha), to pole kwadratu o boku 100 m. 1 ha 10000 m 2 1 ha 100 a

Slide 7

2 Ile 1 m ma milimetrów kwadratowych ? Jeden metr kwadratowy, to pole kwadratu o boku jednego metra. Jeden metr ma sto centymetrów,czyli tysiąc milimetrów. Zatem w 1m2 mieści się 1000 000 kwadratów o boku 1 mm. Możemy więc krótko zapisać zależność: 2 2 1 m 1 000 000 mm

Slide 8

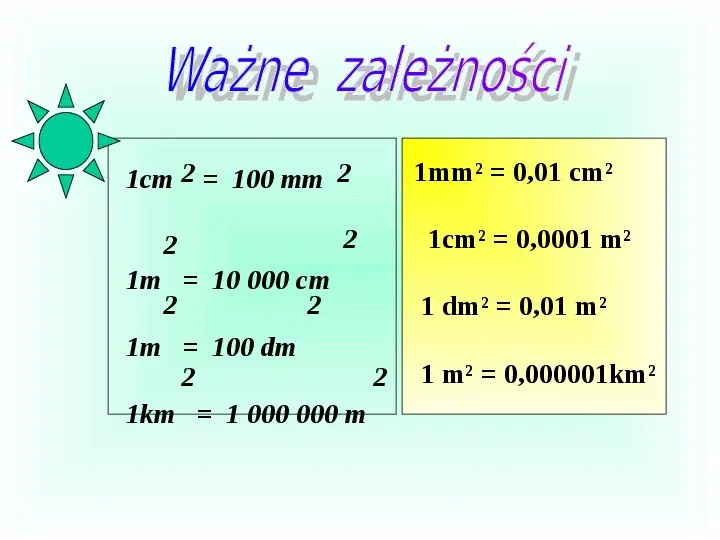
1cm 2 100 mm 2 2 2 1m 10 000 cm 2 2 1m 100 dm 2 2 1km 1 000 000 m 1mm 0,01 cm 1cm 0,0001 m 1 dm 0,01 m 1 m 0,000001km

Slide 9

PLANIMETRIA TO NAUKA O FIGURACH PŁASKICH Długość odcinka możemy zmierzyć za pomocą linijki. Mało kto wie, że przyrząd do mierzenia pól wynalazł niemiecki inżynier J. Hermann. Było to w roku 1814 . Urządzenie nazywa się planimetr. Planimetr najczęściej jest używany przez geodetów do mierzenia powierzchni obszarów na mapach.

Slide 10

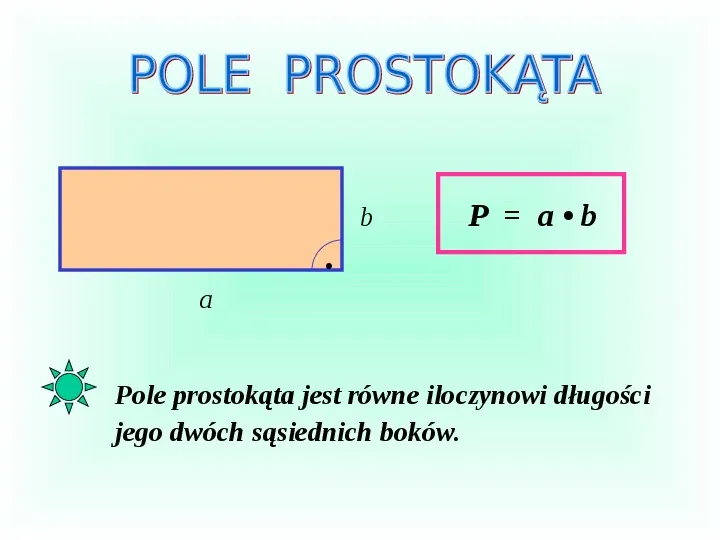
b P ab a Pole prostokąta jest równe iloczynowi długości jego dwóch sąsiednich boków.

Slide 11

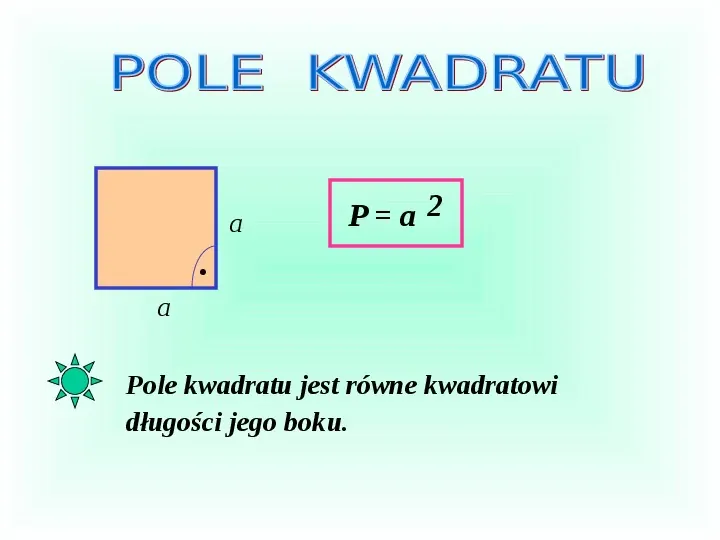
a Pa 2 a Pole kwadratu jest równe kwadratowi długości jego boku.

Slide 12

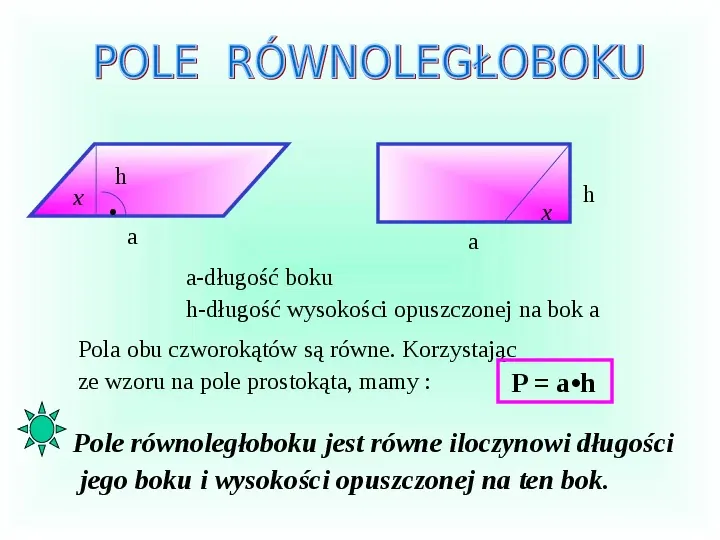
h a x h a x a-długość boku h-długość wysokości opuszczonej na bok a Pola obu czworokątów są równe. Korzystając ze wzoru na pole prostokąta, mamy : P ah Pole równoległoboku jest równe iloczynowi długości jego boku i wysokości opuszczonej na ten bok.

Slide 13

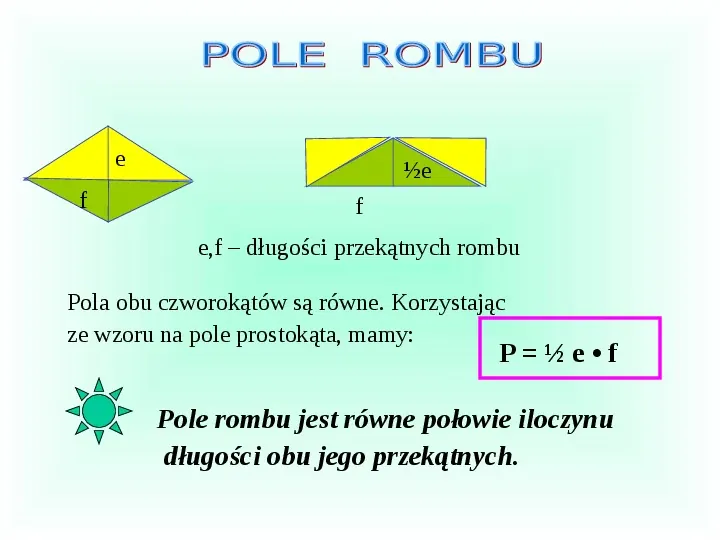
e f e f e,f długości przekątnych rombu Pola obu czworokątów są równe. Korzystając ze wzoru na pole prostokąta, mamy: P ef Pole rombu jest równe połowie iloczynu długości obu jego przekątnych.

Slide 14

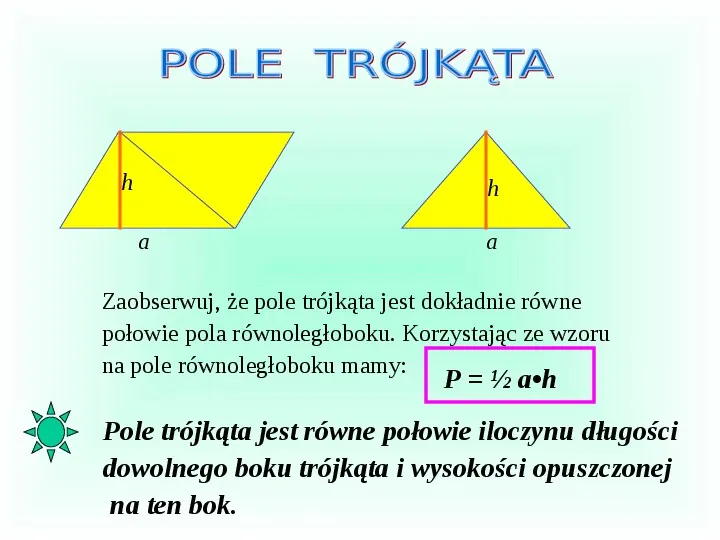
h h a a Zaobserwuj, że pole trójkąta jest dokładnie równe połowie pola równoległoboku. Korzystając ze wzoru na pole równoległoboku mamy: P ah Pole trójkąta jest równe połowie iloczynu długości dowolnego boku trójkąta i wysokości opuszczonej na ten bok.

Slide 15

b a a i b boki leżące na ramionach kąta prostego, czyli przyprostokątne trójkąta P ab Pole trójkąta prostokątnego równe jest połowie iloczynu długości jego przyprostokątnych.

Slide 16

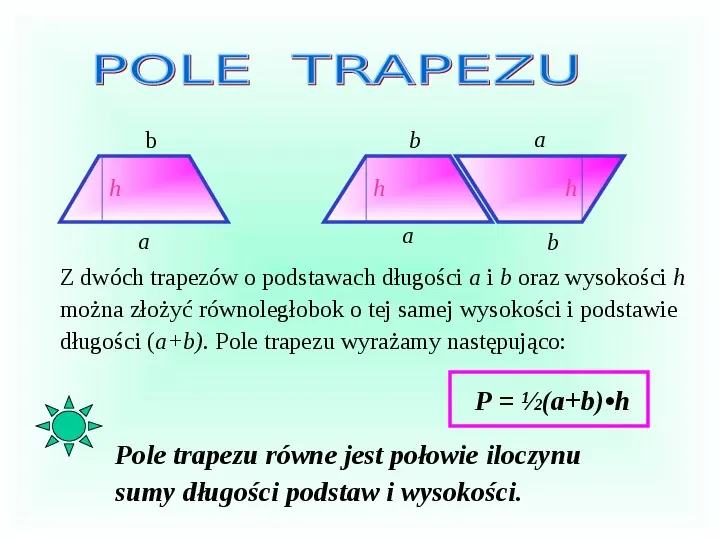
b h b h a h a a b Z dwóch trapezów o podstawach długości a i b oraz wysokości h można złożyć równoległobok o tej samej wysokości i podstawie długości (ab). Pole trapezu wyrażamy następująco: P (ab)h Pole trapezu równe jest połowie iloczynu sumy długości podstaw i wysokości.

Slide 17

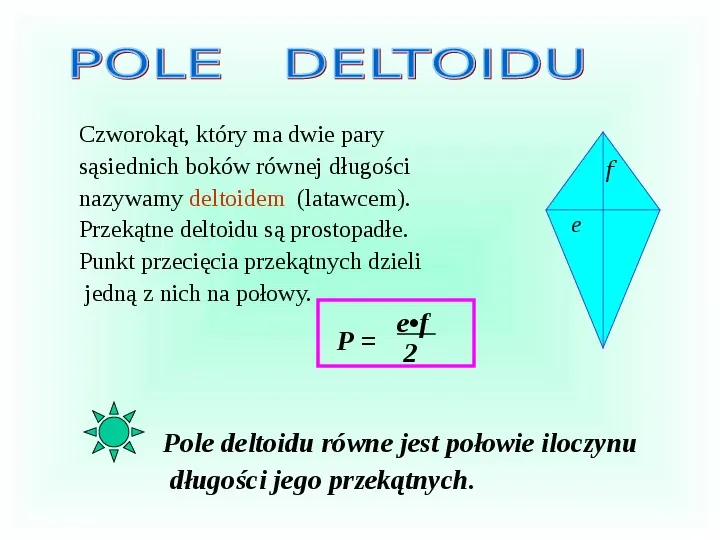
Czworokąt, który ma dwie pary sąsiednich boków równej długości nazywamy deltoidem (latawcem). Przekątne deltoidu są prostopadłe. Punkt przecięcia przekątnych dzieli jedną z nich na połowy. f e ef P 2 Pole deltoidu równe jest połowie iloczynu długości jego przekątnych.

Slide 18

E F D Jak obliczyć pole sześciokąta ABCDEF ? A B C Należy podzielić ten sześciokąt na dwa trójkąty AEF i ABE oraz jeden romb BCDE. Obliczyć pola tych trzech figur i dodać otrzymane wyniki.(Można wykonać inny podział sześciokąta.)

Slide 19

Zadanie 1 Największy skonstruowany na świecie latawiec miał powierzchnię 553 m . Ile to arów? Zadanie 2 Największy wyprodukowany na świecie koc miał powierzchnię 17 289 m. Ile to hektarów?

Slide 20

Zadanie 3 Okno ma powierzchnię 0,8 m. Ile to centymetrów kwadratowych? Zadanie 4 Działka ma powierzchnię 0,03 km. Ile to metrów kwadratowych?

Slide 21

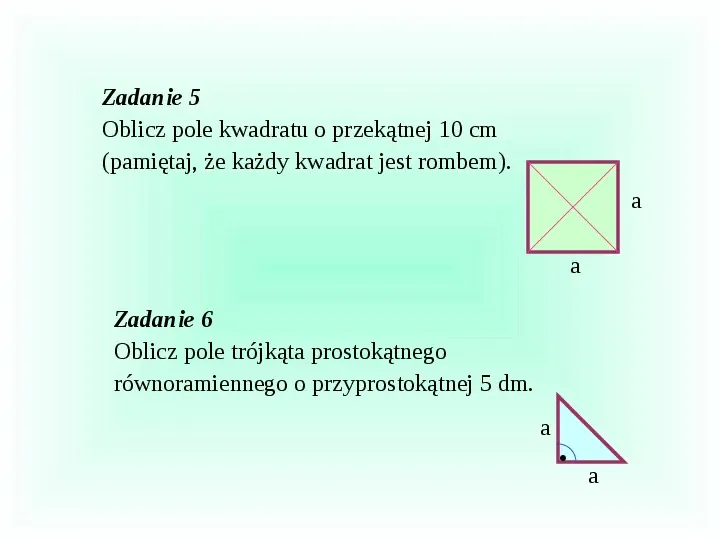
Zadanie 5 Oblicz pole kwadratu o przekątnej 10 cm (pamiętaj, że każdy kwadrat jest rombem). a a Zadanie 6 Oblicz pole trójkąta prostokątnego równoramiennego o przyprostokątnej 5 dm. a a

Slide 22

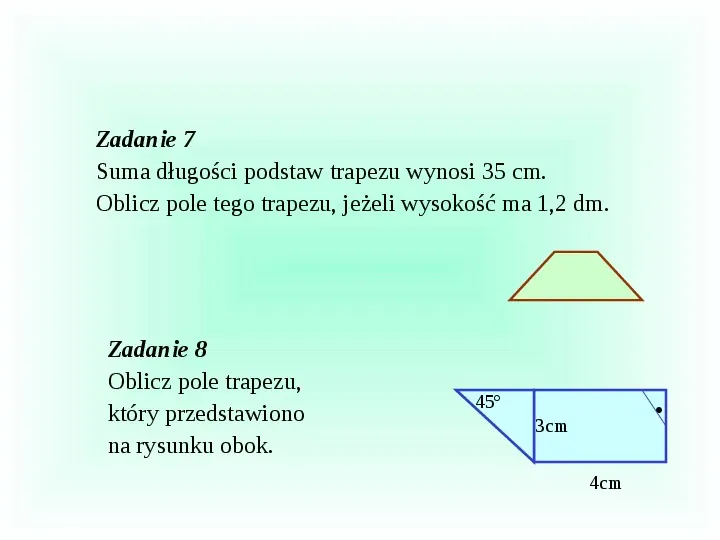
Zadanie 7 Suma długości podstaw trapezu wynosi 35 cm. Oblicz pole tego trapezu, jeżeli wysokość ma 1,2 dm. Zadanie 8 Oblicz pole trapezu, który przedstawiono na rysunku obok. 45 3cm 4cm

Slide 23

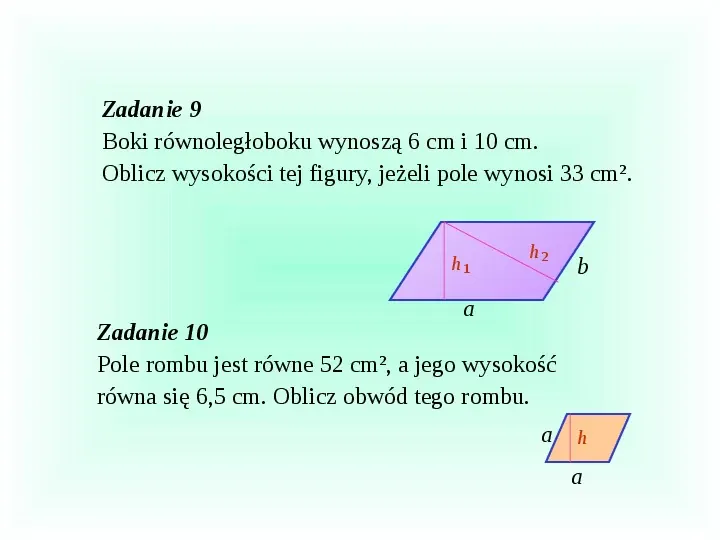
Zadanie 9 Boki równoległoboku wynoszą 6 cm i 10 cm. Oblicz wysokości tej figury, jeżeli pole wynosi 33 cm. h h b a Zadanie 10 Pole rombu jest równe 52 cm, a jego wysokość równa się 6,5 cm. Oblicz obwód tego rombu. a h a

Slide 24

Zadanie 11 Ramiona trapezu prostokątnego mają długości 4cm i 5 cm. Pole trapezu jest równe 92 cm. Oblicz obwód tego trapezu. Zadanie 12 Narysuj w układzie współrzędnych trójkąt KLM o wierzchołkach K(0,0), L(1,-8), M(-3,-4). Oblicz pole tego trójkąta. Odczytaj odpowiednie odcinki z układu wpółrzędnych (nie mierz ich linijką).

Slide 25

Zadanie 1 Zadanie 2 Zadanie 3 Zadanie 4 Zadanie 5 Zadanie 6 Zadanie 7 Zadanie 8 Zadanie 9 Zadanie 10 Zadanie 11 Zadanie 12 5.53 a 1,7289 ha 8 000 cm 30 000 m 50 cm 12,5 dm 210 cm (2,1 dm) 10,5 cm 3,3 cm oraz 5,5 cm 32cm 55cm 14 j

Slide 26

To już koniec drogi uczniu! Mam nadzieję, że podobała Ci się ta lekcja. Jeżeli doszedłeś do tej strony, to znaczy, że dobrze wywiązałeś się z przedstawionych zadań. Dziękuję za Twoją pracę na lekcji. Życzę miłego dnia. Prezentację w całości opracowała i wykonała mgr inż. Anna Berlińska - Komza