Astronomia obserwacyjna

Zobacz slidy

Treść prezentacji

Slide 1

Astronomia obserwacyjna Wykład 4 Ruch planet, komet i sztucznych satelitów Ziemi na sferze niebieskiej 12:31 12:31 1

Slide 2

Układ 2 ciał W opisie ruchu planety wokół Słońca lub księżyca wokół macierzystej planety stosuje się najczęściej przybliżenie 2 punktowych ciał. Jest ono uzasadnione ze względu na: 1. dużą wartość stosunku mas Słońca i planety albo planety i jej księżyca, 2. małe rozmiary ciał względem dzielących je odległości. Dla układu dwóch ciał orbita jednego ciała względem drugiego jest krzywą stożkową (koło, elipsa, parabola, hiperbola). Źródło: Wikipedia 12:31 12:31 2

Slide 3

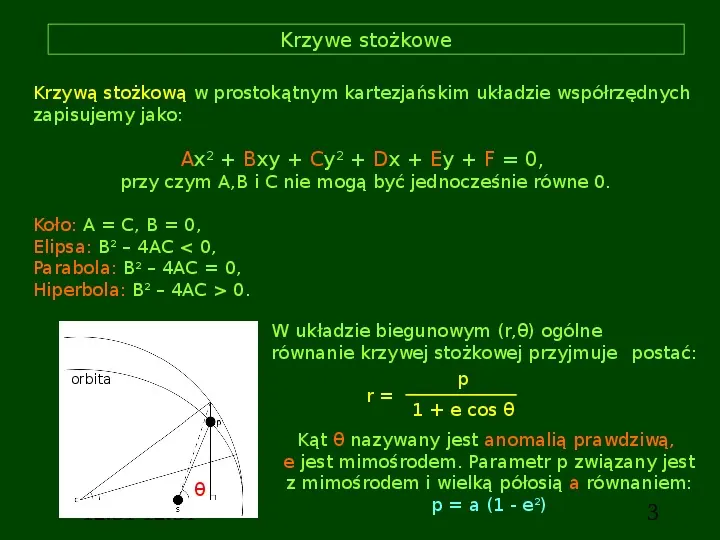
Krzywe stożkowe Krzywą stożkową w prostokątnym kartezjańskim układzie współrzędnych zapisujemy jako: Ax2 Bxy Cy2 Dx Ey F 0, przy czym A,B i C nie mogą być jednocześnie równe 0. Koło: A C, B 0, Elipsa: B2 4AC 0, Parabola: B2 4AC 0, Hiperbola: B2 4AC 0. W układzie biegunowym (r,θ) ogólne równanie krzywej stożkowej przyjmuje postać: p r 1 e cos θ orbita θ 12:31 12:31 Kąt θ nazywany jest anomalią prawdziwą, e jest mimośrodem. Parametr p związany jest z mimośrodem i wielką półosią a równaniem: p a (1 - e2) 3

Slide 4

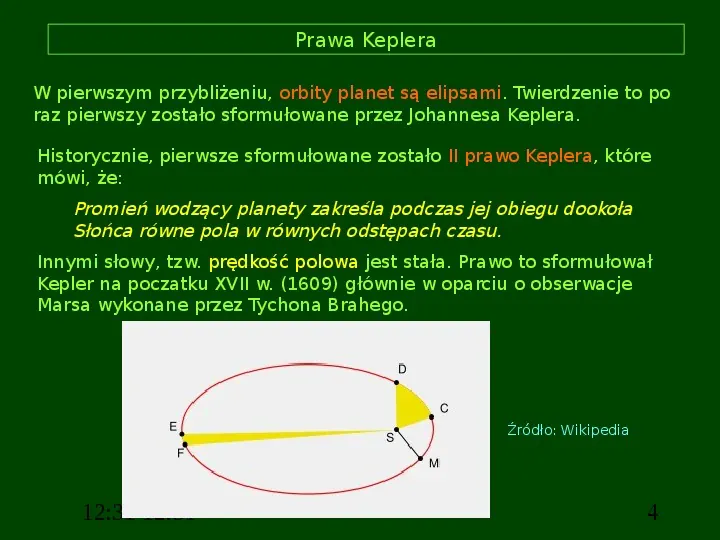
Prawa Keplera W pierwszym przybliżeniu, orbity planet są elipsami. Twierdzenie to po raz pierwszy zostało sformułowane przez Johannesa Keplera. Historycznie, pierwsze sformułowane zostało II prawo Keplera, które mówi, że: Promień wodzący planety zakreśla podczas jej obiegu dookoła Słońca równe pola w równych odstępach czasu. Innymi słowy, tzw. prędkość polowa jest stała. Prawo to sformułował Kepler na poczatku XVII w. (1609) głównie w oparciu o obserwacje Marsa wykonane przez Tychona Brahego. Źródło: Wikipedia 12:31 12:31 4

Slide 5

Prawa Keplera Natomiast I prawo Keplera mówi, że: Wszystkie planety okrążają Słońce po elipsach, mających jedno wspólne ognisko, w którym znajduje się Słońce. Około 10 lat po pierwszych dwóch, Kepler sformułował III prawo, Które zapisuje się tak: Kwadraty czasów obiegów poszczególnych planet dookoła Słońca mają się do siebie tak, jak sześciany ich średnich odległości od Słońca. lub I i II prawo Keplera wyjaśniają zmienną prędkość ruchu planet, natomiast III prawo podaje związek, jaki zachodzi między rzeczywistymi rozmiarami orbit a okresami orbitalnymi. 12:31 12:31 5

Slide 6

III prawo Keplera III prawo Keplera sformułowane w ten sposób nie jest ścisłe, np. a3P2 wyrażone w AU3rok2 wynosi 0,99996 dla Merkurego i 1,00223 dla Jowisza. III prawo Keplera sformułowane ściśle dla dowolnego układu dwóch ciał (także o porównywalnych masach) nazywa się uogólnionym III prawem Keplera i wygląda tak: gdzie G jest stałą grawitacji, a M1 i M2 oznaczają dwie masy dwu ciał krążących wokół środka ich masy (barycentrum). V a-12 Dla planet M1M2 zmienia się niewiele, bo M MP M 12:31 12:31 6

Slide 7

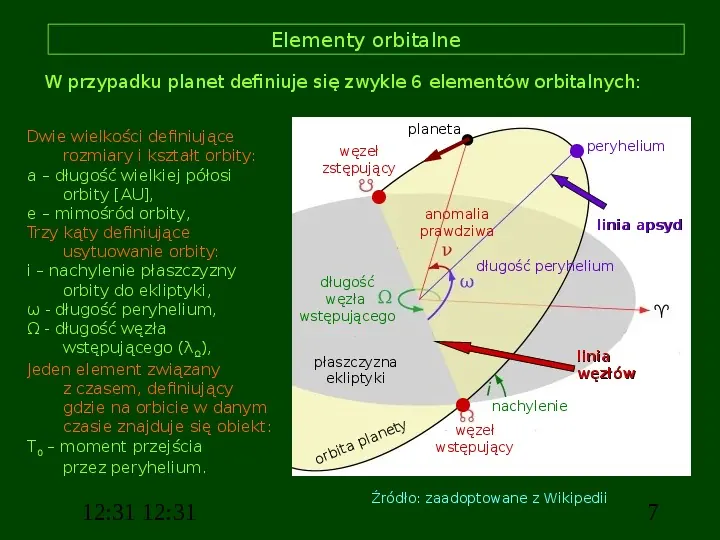
Elementy orbitalne W przypadku planet definiuje się zwykle 6 elementów orbitalnych: Dwie wielkości definiujące rozmiary i kształt orbity: a długość wielkiej półosi orbity [AU], e mimośród orbity, Trzy kąty definiujące usytuowanie orbity: i nachylenie płaszczyzny orbity do ekliptyki, ω - długość peryhelium, Ω - długość węzła wstępującego (λΩ), Jeden element związany z czasem, definiujący gdzie na orbicie w danym czasie znajduje się obiekt: T0 moment przejścia przez peryhelium. 12:31 12:31 planeta peryhelium węzeł zstępujący anomalia prawdziwa długość peryhelium długość węzła wstępującego linia węzłów płaszczyzna ekliptyki i ta orb ne pla ty linia apsyd nachylenie węzeł wstępujący Źródło: zaadoptowane z Wikipedii 7

Slide 8

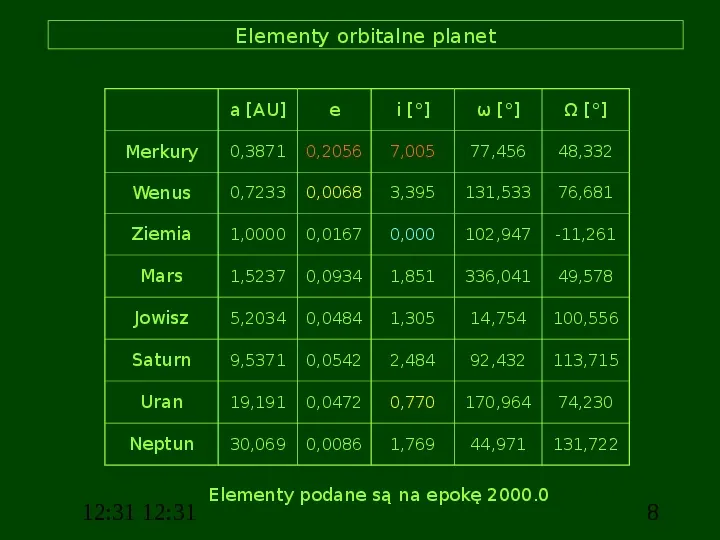
Elementy orbitalne planet a [AU] e i [] ω [] Ω [] Merkury 0,3871 0,2056 7,005 77,456 48,332 Wenus 0,7233 0,0068 3,395 131,533 76,681 Ziemia 1,0000 0,0167 0,000 102,947 -11,261 Mars 1,5237 0,0934 1,851 336,041 49,578 Jowisz 5,2034 0,0484 1,305 14,754 100,556 Saturn 9,5371 0,0542 2,484 92,432 113,715 Uran 19,191 0,0472 0,770 170,964 74,230 Neptun 30,069 0,0086 1,769 44,971 131,722 12:31 12:31 Elementy podane są na epokę 2000.0 8

Slide 9

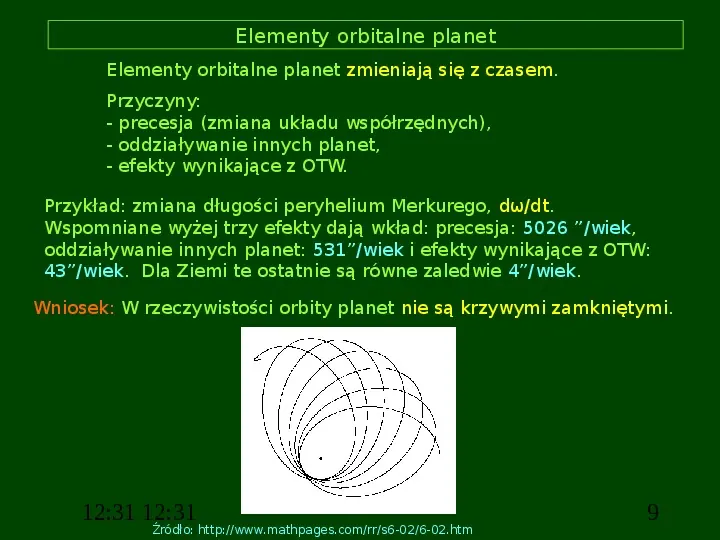
Elementy orbitalne planet Elementy orbitalne planet zmieniają się z czasem. Przyczyny: - precesja (zmiana układu współrzędnych), - oddziaływanie innych planet, - efekty wynikające z OTW. Przykład: zmiana długości peryhelium Merkurego, dωdt. Wspomniane wyżej trzy efekty dają wkład: precesja: 5026 wiek, oddziaływanie innych planet: 531wiek i efekty wynikające z OTW: 43wiek. Dla Ziemi te ostatnie są równe zaledwie 4wiek. Wniosek: W rzeczywistości orbity planet nie są krzywymi zamkniętymi. 12:31 12:31 Źródło: http:www.mathpages.comrrs6-026-02.htm 9

Slide 10

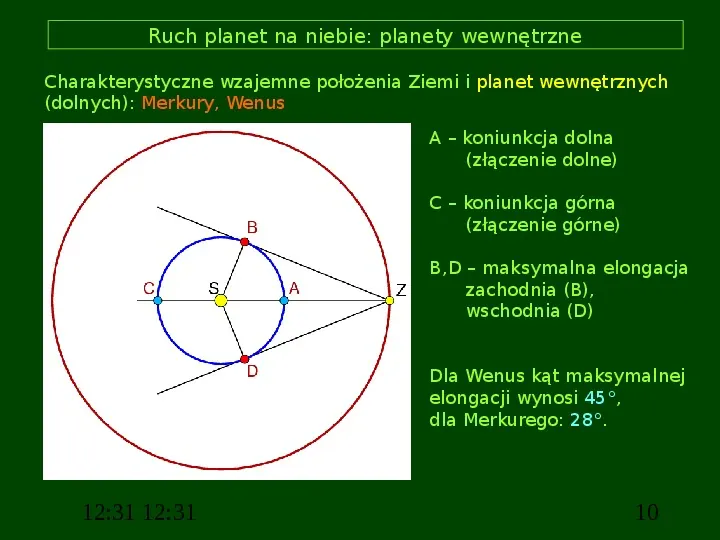
Ruch planet na niebie: planety wewnętrzne Charakterystyczne wzajemne położenia Ziemi i planet wewnętrznych (dolnych): Merkury, Wenus A koniunkcja dolna (złączenie dolne) C koniunkcja górna (złączenie górne) B,D maksymalna elongacja zachodnia (B), wschodnia (D) Dla Wenus kąt maksymalnej elongacji wynosi 45, dla Merkurego: 28. 12:31 12:31 10

Slide 11

Ruch planet na niebie: planety wewnętrzne Planety wewnętrzne przechodzą cały zakres faz, które obserwujemy u Księżyca. Dodatkowo (zwłaszcza dla Wenus) zmiany odległości od Ziemi są duże, co powoduje także duże zmiany rozmiarów kątowych tych planet. Dla Wenus: 0,255 1,745 AU (6,8) Dla Merkurego: 0,517 1,483 AU (2,9) Białkowska kolekcja obrazów Wenus zebrana przez G.Kopackiego 12:31 12:31 11

Slide 12

Ruch planet na niebie: planety wewnętrzne Podczas koniunkcji dolnej może dochodzić do przejść planet wewnętrznych przed tarczą Słońca (podczas koniunkcji górnej planeta może przejść za tarczą Słońca). Dodatkowy warunek: planeta musi się znajdować blisko węzła orbity. tranzyt Merkurego 7 maja 2003 12:31 12:31 tranzyt Wenus 8 czerwca 2004 Źródło: APOD 12

Slide 13

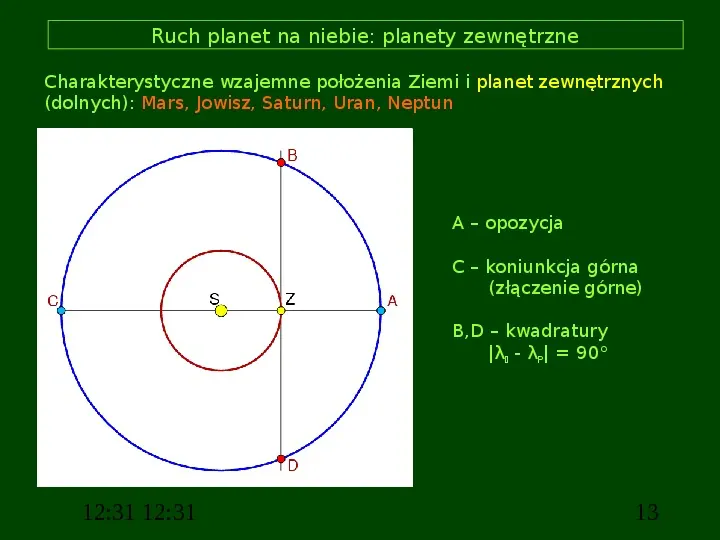
Ruch planet na niebie: planety zewnętrzne Charakterystyczne wzajemne położenia Ziemi i planet zewnętrznych (dolnych): Mars, Jowisz, Saturn, Uran, Neptun A opozycja C koniunkcja górna (złączenie górne) B,D kwadratury λ - λP 90 12:31 12:31 13

Slide 14

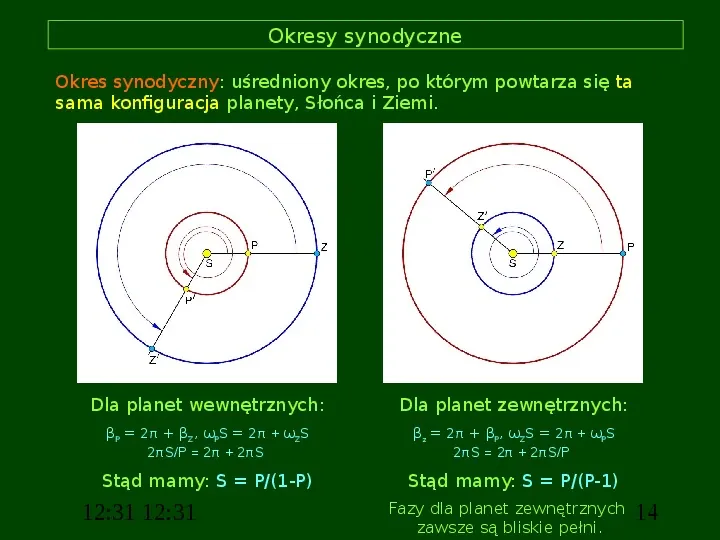
Okresy synodyczne Okres synodyczny: uśredniony okres, po którym powtarza się ta sama konfiguracja planety, Słońca i Ziemi. Dla planet wewnętrznych: Dla planet zewnętrznych: βP 2π βZ, ωPS 2π ωZS 2πSP 2π 2πS βz 2π βP, ωZS 2π ωPS 2πS 2π 2πSP Stąd mamy: S P(1-P) Stąd mamy: S P(P-1) 12:31 12:31 Fazy dla planet zewnętrznych zawsze są bliskie pełni. 14

Slide 15

Pozorne ruchy planet: ruch wsteczny Ruch planety na tle gwiazd może być dość skomplikowany. W szczególności, planeta taka może poruszać się ruchem wstecznym (maleje jej długość ekliptyczna) i zataczać pętle na niebie. Tutaj: Mars i Uran Źródło: Wikipedia 12:31 12:31 15

Slide 16

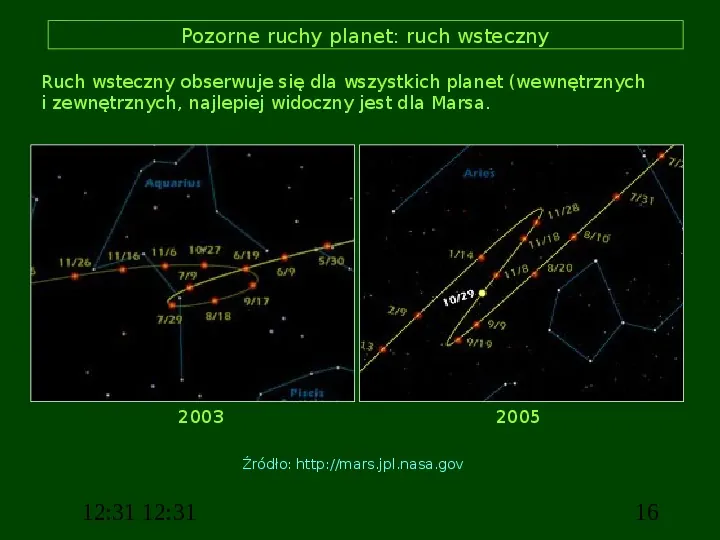
Pozorne ruchy planet: ruch wsteczny Ruch wsteczny obserwuje się dla wszystkich planet (wewnętrznych i zewnętrznych, najlepiej widoczny jest dla Marsa. 2003 2005 Źródło: http:mars.jpl.nasa.gov 12:31 12:31 16

Slide 17

Planety Źródło: http:www.nineplanets.plintro.html 12:31 Więcej wiadomości o planetach: kurs fizyka układów planetarnych, semestr 4 12:31 17

Slide 18

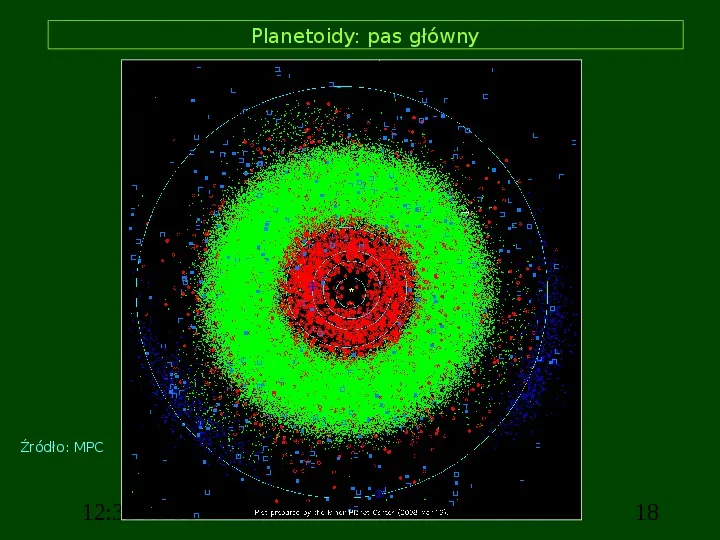
Planetoidy: pas główny Źródło: MPC 12:31 12:31 18

Slide 19

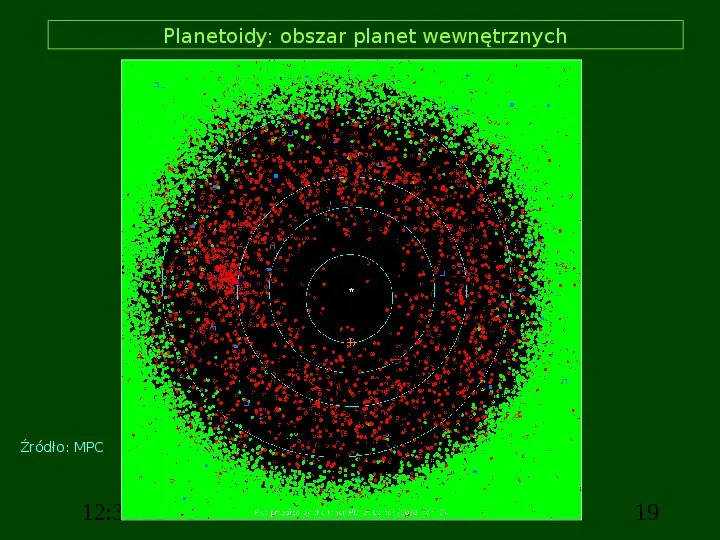
Planetoidy: obszar planet wewnętrznych Źródło: MPC 12:31 12:31 19

Slide 20

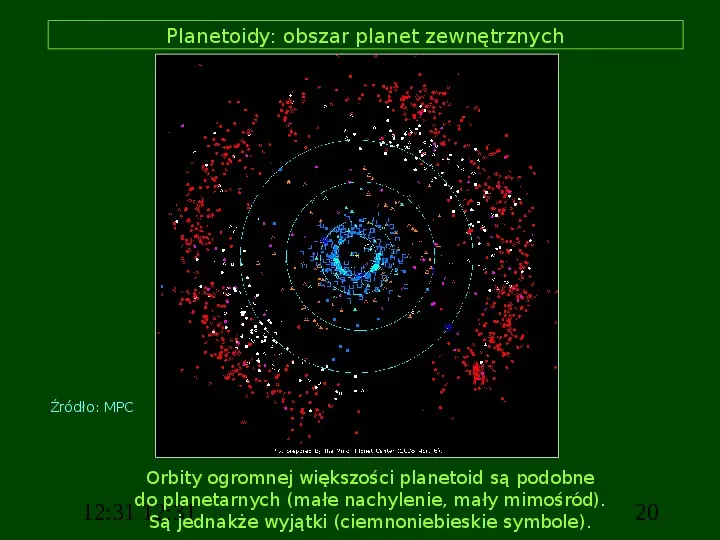
Planetoidy: obszar planet zewnętrznych Źródło: MPC Orbity ogromnej większości planetoid są podobne do planetarnych (małe nachylenie, mały mimośród). 12:31 12:31 Są jednakże wyjątki (ciemnoniebieskie symbole). 20

Slide 21

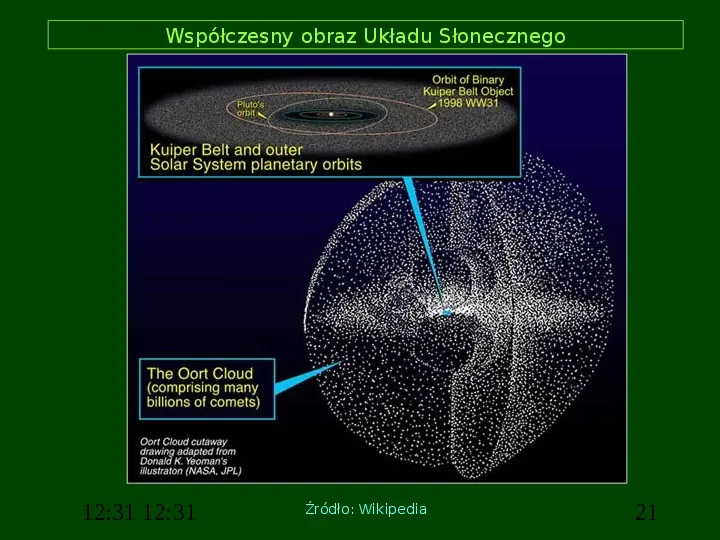
Współczesny obraz Układu Słonecznego 12:31 12:31 Źródło: Wikipedia 21

Slide 22

Komety Obserwowane orbity komet to najczęściej orbity eliptyczne lub eliptyczne, bliskie parabolicznym. Te o najmniejszych mimośrodach mają najczęściej cechy orbitalne podobne do planetoid (ruch prosty, niewielkie nachylenia). Jeśli okres orbitalny jest krótszy niż 200 lat nazywa się je krótkookresowymi. Znamy obecnie ponad 3,000 komet, z których kilkaset to komety krótkookresowe. Źródło: Wikipedia 12:31 12:31 1P Halley: P 75,2 roku a 17,8 AU (0,586 - 35,1 AU) e 0,967 i 162,3 2P Encke: P 3,30 roku a 2,218 AU (0,330 4,11 AU) e 0,847 i 11,8 73P Schwassmann-Wachmann 3: P 5,35 roku a 3,06 AU (0,939 5,19 AU) e 0,693 i 11,4 22

Slide 23

Komety Inne komety, to: długookresowe, orbity eliptyczne, ale mimośrody bardzo bliskie okresy szacowane są na dziesiątki tysięcy a nawet miliony lat. Niewątpliwie związane są jednak z Układem Słonecznym. jednopojawieniowe o orbitach parabolicznych albo nawet hiperbolicznych. Orbita hiperboliczna mogłaby świadczyć, że kometa pochodzi spoza US. Najczęściej jednak jest to kometa pochodząca z dalekich obszarów US (obłok Oorta), której orbita może stać się hiperboliczna wskutek oddziaływania z planetami (głównie Jowiszem). Komety głównego pasa: orbity podobne do obiektów głównego pasa planetoid. Kometa Hyakutake 12:31 12:31 Źródło: Wikipedia 23

Slide 24

Układ Ziemia - Księżyc Układ Ziemia-Księżyc nazywa się niekiedy planetą podwójną, ze względu na dość duży stosunek mas. Masa Księżyca stanowi 1,215 masy układu Ziemia-Księżyc (MZMK 81,3). Masa tego układu wynosi 6,049 1024 kg. Promień równikowy Księżyca (1737 km) stanowi 27 promienia równikowego Ziemi (6378 km). Średnia gęstość Księżyca wynosi około 3,34 gcm3, Ziemi: 5,52 gcm3 Środek masy układu Ziemia-Księżyc znajduje się wewnątrz Ziemi, średnio 4671 km od jej środka. Okres obrotu Księżyca wokół osi jest równy okresowi obiegu wokół Ziemi (27,3217 d): ta synchroniczność wymuszona została siłami pływowymi. Orbita Księżyca jest eliptyczna (e 0,0549, a 384 402 km). Odległość Księżyca zmienia się w granicach od 363 do 406 tys. km. 12:31 12:31 24

Slide 25

Libracja Księżyca Libracja: w długości i szerokości Źródło: APOD 12:31 12:31 25

Slide 26

Układ Ziemia - Księżyc Nachylenie orbity Księżyca do ekliptyki wynosi średnio 509. Wskutek oddziaływań perturbacyjnych pochodzących od Słońca, linia węzłów orbity Księżyca wędruje bardzo szybko. Węzły orbity Księżyca cofają się po ekliptyce. Jeden pełny obrót linii węzłów trwa 18,6 roku. W wyniku tego cofania miesiąc smoczy (od węzła do węzła) jest krótszy niż miesiąc gwiazdowy i wynosi 27,2122 d. Oprócz tego obserwujemy szybki ruch linii apsyd, w kierunku zgodnym z ruchem Księżyca po orbicie. Z tego względu miesiąc anomalistyczny (od perygeum do perygeum) jest dłuższy niż miesiąc gwiazdowy i wynosi 27,5546 d. Pełny obrót linii apsyd trwa 8,85 roku. cykl zakryć Plejad 12:31 12:31 26

Slide 27

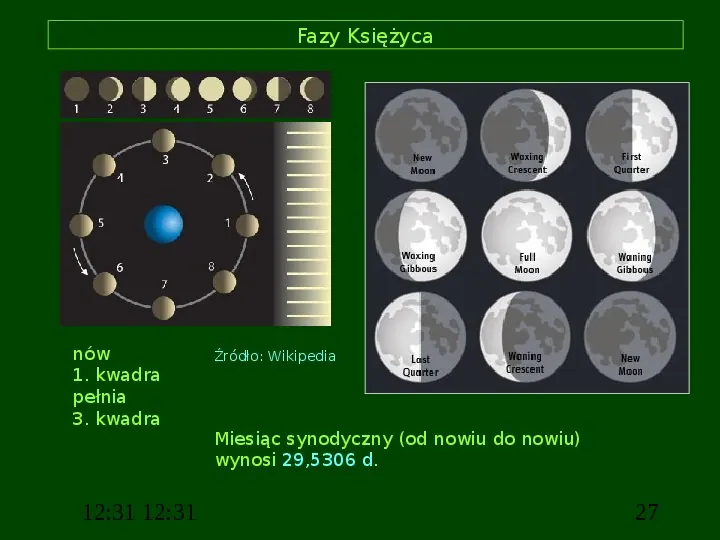
Fazy Księżyca nów 1. kwadra pełnia 3. kwadra 12:31 12:31 Źródło: Wikipedia Miesiąc synodyczny (od nowiu do nowiu) wynosi 29,5306 d. 27

Slide 28

Światło popielate Księżyca Źródło: APOD, Vic Winter 12:31 12:31 28

Slide 29

Zaćmienia w układzie Ziemia-Księżyc Z uwagi na małe nachylenie orbity Księżyca, w układzie Ziemia-Księżyc-Słońce dochodzi do zaćmień, tym bardziej, że średnice kątowe Słońca i Księżyca są podobne. Słońca: między 3137 a 3231. Księżyca: między 2955 a 3328. Do zaćmień może dojść tylko wtedy, kiedy Księżyc w pełni lub nowiu znajduje się blisko węzłów swojej orbity. Powtarzalność zjawisk zaćmień może następować co wartość, która jest w przybliżeniu wielokrotnością miesiąca smoczego (27,2122 d) i synodycznego (29,5306 d). Np. 13 Msm (353,759 d) 12 Msyn (354,367 d), Δ 0,608 d. Astronomowie chaldejscy znaleźli lepszą współmierność: 223 Msyn (6585,324 d) 242 Msm (6585,352 d, Δ 0,028 d) 18 lat 11 dni 1 saros. Po okresie sarosu powtarzają się zaćmienia o podobnych cechach. W czasie 1 sarosu dochodzi do około 70 zaćmień, w tym około 42 to Zaćmienia Słońca, a 28 zaćmienia Księżyca. 12:31 12:31 29

Slide 30

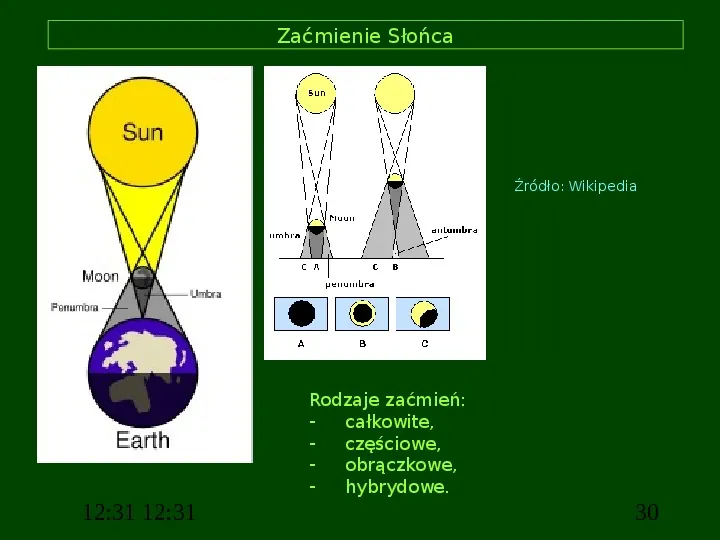
Zaćmienie Słońca Źródło: Wikipedia Rodzaje zaćmień: całkowite, częściowe, obrączkowe, hybrydowe. 12:31 12:31 30

Slide 31

Zaćmienie Słońca Źródło: Wikipedia 12:31 12:31 31

Slide 32

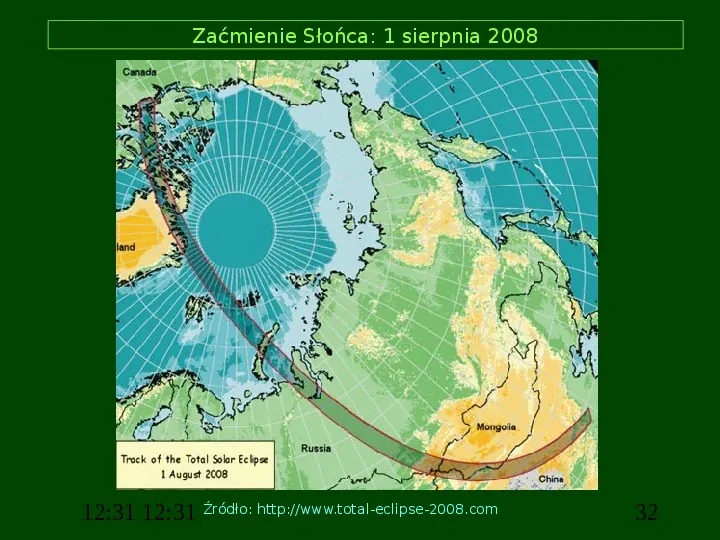
Zaćmienie Słońca: 1 sierpnia 2008 12:31 12:31 Źródło: http:www.total-eclipse-2008.com 32

Slide 33

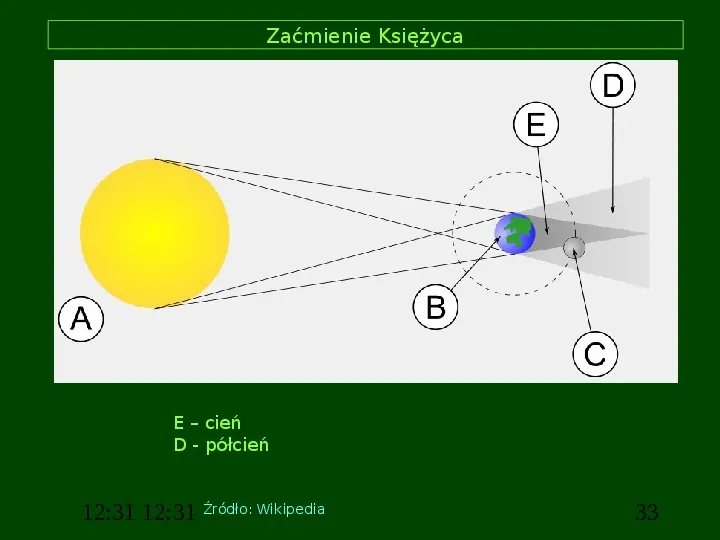
Zaćmienie Księżyca E cień D - półcień 12:31 12:31 Źródło: Wikipedia 33

Slide 34

Zaćmienie Księżyca 12:31 12:31 Źródło: Wikipedia 34

Slide 35

Sztuczne satelity Ziemi Sztuczne satelity Ziemi można podzielić ze względu na przeznaczenie (komunikacyjne, nawigacyjne, meteorologiczne, obserwatoria satelitarne, wojskowe, szpiegowskie i inne). Ze względu na orbitę satelity możemy je podzielić na: - położenie centrum (geocentryczne, heliocentryczne, galaktocentryczne, inne). - wysokość orbity (niskie, do 2000 km, średnie (pow. 2000 km), wysokie (pow. Orbity geocentrycznej). - nachylenie płaszczyzny orbity do równika (biegunowa). - mimośród (kołowa, eliptyczna, paraboliczna, hiperboliczna) - synchroniczność (geostacjonarna, geosynchroniczna, półsynchroniczna (12 h), podsynchroniczna, nadsynchroniczna, - specjalne (halo, Lissajous: w okolicach punktów Lagrangea, transferowa do Księżyca. 12:31 12:31 Źródło: MPC 35

Slide 36

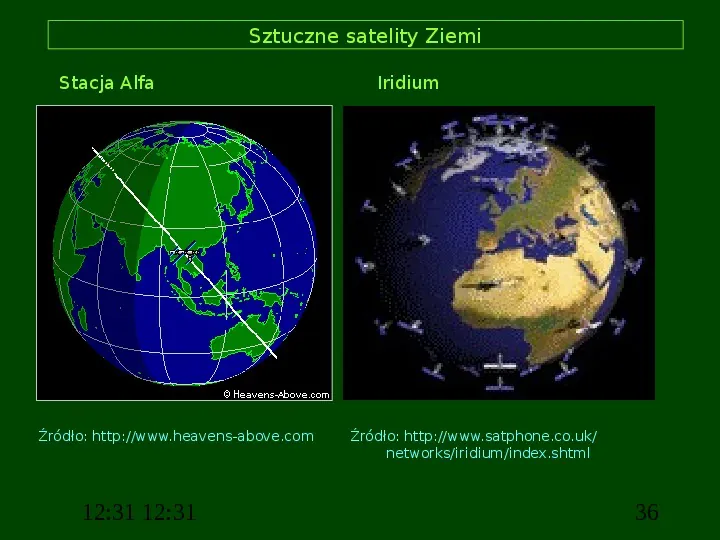
Sztuczne satelity Ziemi Stacja Alfa Źródło: http:www.heavens-above.com 12:31 12:31 Iridium Źródło: http:www.satphone.co.uk networksiridiumindex.shtml 36