Twierdzenie Talesa

Zobacz slidy

Treść prezentacji

Slide 1

Twierdzenie Talesa Opracowała: Alina Kaczmarczyk

Slide 2

Twierdzenie Talesa

Slide 3

Spis treści: Twierdzenie Talesa. Z historii... O Talesie. Zadania. Karta odpowiedzi do zadań.

Slide 4

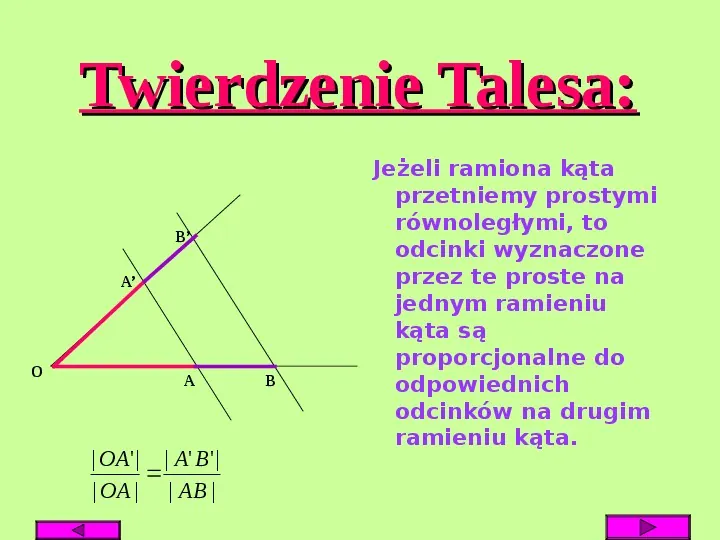
Twierdzenie Talesa: B A O A OA A B OA AB B Jeżeli ramiona kąta przetniemy prostymi równoległymi, to odcinki wyznaczone przez te proste na jednym ramieniu kąta są proporcjonalne do odpowiednich odcinków na drugim ramieniu kąta.

Slide 5

Tales z Miletu Tales z Miletu ( ok. 640-546 p.n.e.) jest uważany za jednego z siedmiu najwybitniejszych mędrców starożytności. Był nie tylko filozofem, ale także matematykiem i astronomem. Potrafił podobno przewidywać zaćmienia Słońca i Księżyca. Prawdopodobnie przewidziane przez niego zaćmienie Słońca w dniu 28 V 585 r.p.n.e. Wpłynęło na przebieg bitwy nad rzeką Halys. Podobno Tales jako pierwszy ustalił, że rok trwa 365 dni. Określił także, w jaki sposób można kierować się w nawigacji położeniem gwiazd Małego Wozu. Oprócz twierdzenia odkrył także, że kąt wpisany oparty na średnicy okręgu jest kątem prostym. W wielu krajach właśnie to twierdzenie nazywane jest twierdzeniem Talesa.

Slide 6

Zadania

Slide 7

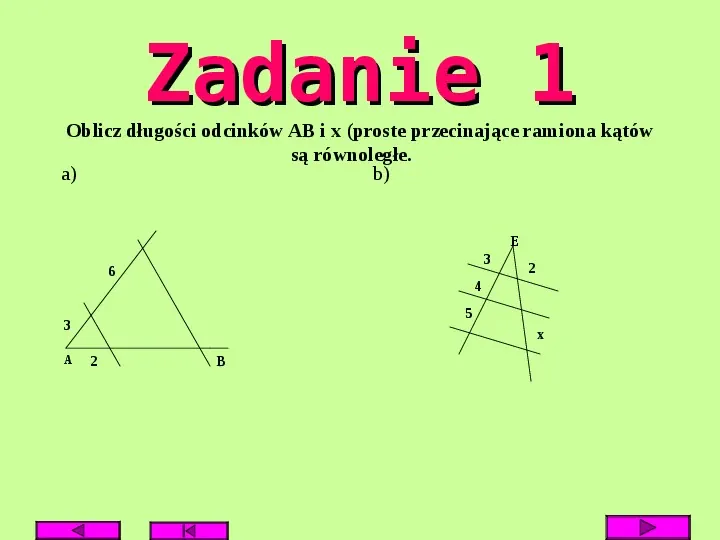
Zadanie 1 Oblicz długości odcinków AB i x (proste przecinające ramiona kątów są równoległe. a) b) E 3 6 4 5 3 A 2 x 2 B

Slide 8

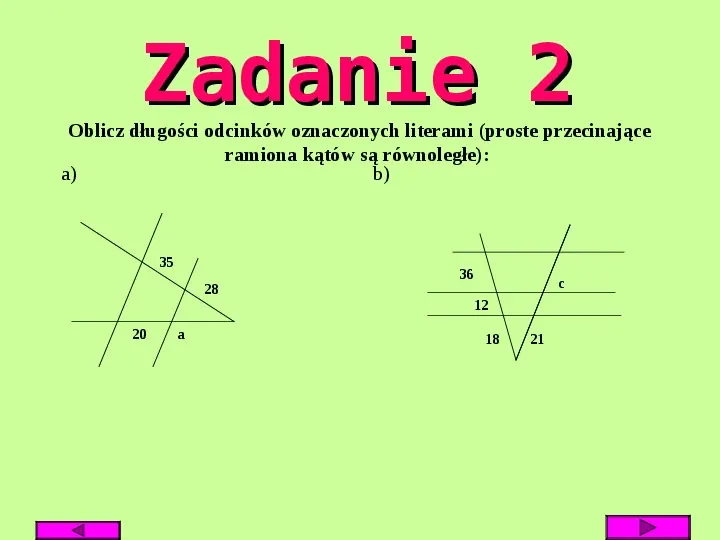
Zadanie 2 Oblicz długości odcinków oznaczonych literami (proste przecinające ramiona kątów są równoległe): a) b) 35 36 c 28 12 20 a 18 21

Slide 9

Zadanie 3 Popatrz na rysunek obok. Znajdź brakujące wyrazy proporcji (proste k i l są równoległe). a) t z b) b a x c) y l k d) x x y z ? a b z ? t ? z t ? x ? a ?

Slide 10

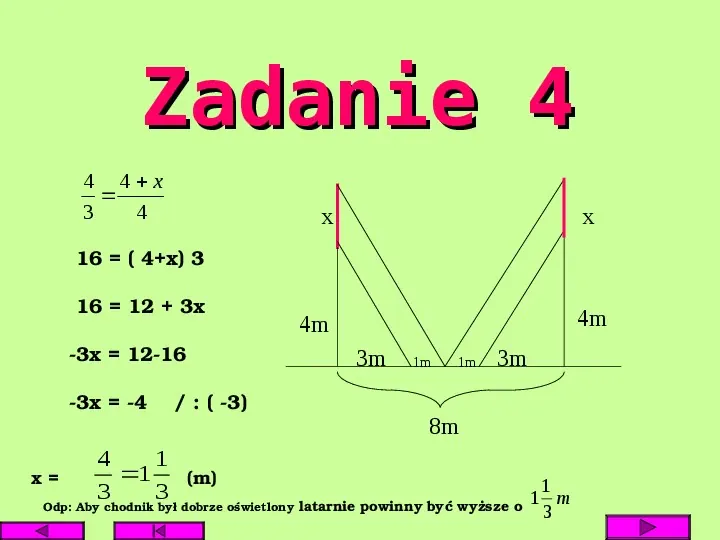
Zadanie 4 Na chodniku przy pewne ulicy ustawiono latarnie o wysokości 4 m, w odstępach co 8 m. Okazało się, że wysokość latarni została źle dobrana, gdyż między nimi pozostają na chodniku nieoświetlone pasy szerokości 2 m. O ile wyższe powinny być latarnie, aby chodnik był dobrze oświetlony?

Slide 11

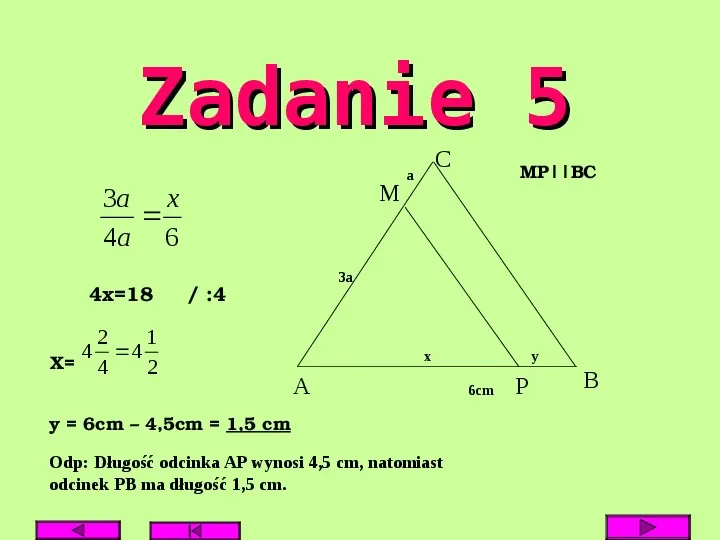
Zadanie 5 W trójkącie ABC bok AB ma długość 6 cm. Na boku AC zaznaczono punkt M taki, że odcinek AM jest trzy razy dłuższy od odcinka MC. Przez punkt M poprowadzono prostą równoległą do boku BC, która przecięła bok AB w punkcie P. Oblicz długości odcinków AP i PB.

Slide 12

Karta odpowiedzi Zadanie Zadanie Zadanie Zadanie Zadanie 1 2 3 4 5

Slide 13

Zadanie 1 a)     2 3 AB 9 3AB 18 : 3   AB 6 b) 3 5 2 x 3 x 10 : 3 1 x 3 3

Slide 14

Zadanie 2 a) a 20 28 35 a 4 28 7                  7a  284    :7           a  44           a  16  b) c 36 21 18 c 2 21 1 c  42

Slide 15

Zadanie 3 a)       b)  x x y z z t a b z z t c)  y t z t x y d)  x xy a b

Slide 16

Zadanie 4 4 4x 3 4 x x           16  ( 4x) 3           16  12  3x          3x  1216            3x  4     : ( 3)  x   4 1 1 3 3 (m) 4m 4m 3m 1m 1m 3m 8m 1 1  Odp: Aby chodnik był dobrze oświetlony latarnie powinny być wyższe o  3 m

Slide 17

Zadanie 5 M 3a x 4a 6         MPBC 3a             4x18      :4 2 1      4 4        X 4 2 C a x A y  6cm  4,5cm  1,5 cm Odp: Długość odcinka AP wynosi 4,5 cm, natomiast odcinek PB ma długość 1,5 cm. y 6cm P B