Konstrukcje geometryczne na płaszczyźnie

Zobacz slidy

Treść prezentacji

Slide 1

Konstrukcje geometryczne 10 listopada 2000

Slide 2

Konstrukcje geometryczne na płaszczyźnie. MENU Cele pracy cele Opis pracy O konstrukcjach geometrycznych k. g. Konstrukcje elementarne k. el. Wielokąty foremne Zdania konstrukcyjne Okrąg wpisany i opisany na wielokącie Jednokładność, tw. Talesa, tw. Pitagorasa zad. k. okręgi zast. w. for. KONIEC

Slide 3

CELE PRACY Problemy matematyczne towarzyszą ludziom od czasów antycznych po dzień dzisiejszy. Matematyka jest bowiem obecna w wielu dziedzinach działalności człowieka, niezbędna w wykonywaniu wielu zawodów, służy rozwijaniu kwalifikacji i kompetencji intelektualnych. Wielu uczniów boryka się z problemami w przyswajaniu wiedzy matematycznej. Lekcje matematyki wydają się im niezrozumiałe i nudne. Z myślą o nich stworzyłam tę prezentację, która, mam nadzieję, uatrakcyjni zajęcia lekcyjne. Głównym celem prezentacji jest stworzenie pomocy dydaktycznej z zakresu treści dotyczących konstrukcji geometrycznych na płaszczyźnie.

Slide 4

Poszczególne slajdy zamierzam wykorzystać na zajęciach, na których uczniowie: uczą się rozwiązywać zadania konstrukcyjne z uwzględnieniem wszystkich etapów rozwiązania (patrz Zadania) wykonują typowe konstrukcje geometryczne (patrz Konstrukcje elementarne) poznają wielokąty foremne i ich własności stosują tw. Pitagorasa, tw. Talesa i własności jednokładności w wykonywaniu konstrukcji konstruują okręgi: wpisany w wielokąt i opisany na wielokącie MENU

Slide 5

KONSTRUKCJE GEOMETRYCZNE Wykonanie konstrukcji polega na narysowaniu figury geometrycznej spełniającej podane warunki, przy pomocy określonych przyrządów konstrukcyjnych. Historycznie ujmując, najstarszymi konstrukcjami geometrycznymi są konstrukcje za pomocą cyrkla i linijki, zw. również konstrukcjami klasycznymi lub konstrukcjami platońskimi. Takie konstrukcje umożliwiają poprowadzenie prostej przez dane dwa punkty, konstrukcję okręgu o danym środku i danym promieniu, znalezienie punktów przecięcia wykreślonych prostych i okręgów oraz wybór dowolnego punktu na skonstruowanej linii (prostej lub okręgu). Konstrukcjami klasycznymi są np. KONSTRUKCJA SYMETRALNEJ ODCINKA KONSTRUKCJA DWUSIECZNEJ KĄTA MENU

Slide 6

Nie wszystkie zadania konstrukcyjne dają się wykonać metodą cyrkla i linijki [konstrukcje niewykonalne]; niektóre zadania konstrukcyjne można wykonać przy jeszcze większym ograniczeniu środków niż w metodzie cyrkla i linijki [konstrukcje Mohra-Mascheroniego]. Analogiczna do metody cyrkla i linijki na płaszczyźnie metoda k.g. w przestrzeni pozwala: poprowadzić płaszczyznę przez trzy dane niewspółliniowe punkty, skonstruować sferę o danym środku i o danym promieniu, znaleźć linię przecięcia dwóch skonstruowanych powierzchni (płaszczyzn i sfer), wybrać dowolny punkt na skonstruowanej powierzchni, poprowadzić prostą przez dane dwa punkty oraz wykonać dowolną konstrukcję geometryczną metodą cyrkla i linijki na utworzonej powierzchni. MENU

Slide 7

KONSTRUKCJE NIEWYKONALNE Konstrukcje niewykonalne to tradycyjne określenie zadań konstrukcyjnych, których nie można wykonać za pomocą cyrkla i linijki. Przykładami konstrukcji niewykonalnych są trzy sławne zadania konstrukcyjne sformułowane w starożytnej Grecji: Podwojenie sześcianu Trysekcja kąta Kwadratura koła Zadania te zostały przez starożytnych Greków rozwiązane. Wątpliwości wzbudził sposób przeprowadzenia tych konstrukcji (użyte przyrządy konstrukcyjne). Wybitny filozof grecki Platon (IV w p.n.e.), który w założonej przez siebie Akademii zajmował się również konstrukcjami geometrycznymi, ustalił, że konstrukcje można wykonywać, posługując się wyłącznie cyrklem i linijką (bez podziałki). Autorytet Platona był tak wielki, że podane przez niego ograniczenia przyjęły się powszechnie. Wówczas okazało się, że rozwiązania trzech powyższych zadań stały się nieaktualne. Przez kolejne wieki próbowano te zadania rozwiązać posługując się cyrklem i linijką. Dopiero w XIX w. Udowodniono, że takich konstrukcji wykonać nie można. Termin kwadratura koła wszedł nawet do języka potocznego na określenie sprawy, której nie sposób rozwiązać. MENU

Slide 8

PODWOJENIE SZEŚCIANU ( problem delijski ) Zbudować sześcian o objętości dwa razy większej niż objętość danego sześcianu. Nazwa problem delijski, jak głosi legenda, wiąże się z problemem, który mieli rozstrzygnąć mieszkańcy wyspy Delos (obecnie Dilos). Aby uchronić wyspę przed nieszczęściami i przebłagać bogów, musieli oni zbudować ołtarz dwa razy większy od ołtarza znajdującego się w świątyni Apollina. Architekci, nie mogąc rozwiązać tego problemu zwrócili się do matematyków, którzy sprowadzili go do podwojenia sześcianu. Zadanie podwojenia sześcianu polega na konstrukcji odcinka o długości 3a 2 , gdzie a jest długością odcinka danego. Konstrukcja ta jest konstrukcją niewykonalną za pomocą cyrkla i linijki, ponieważ liczba 3 2 nie jest liczbą konstruowalną. Uczony grecki Eratostenes z Cyreny zbudował przyrząd mezolabium. MENU

Slide 9

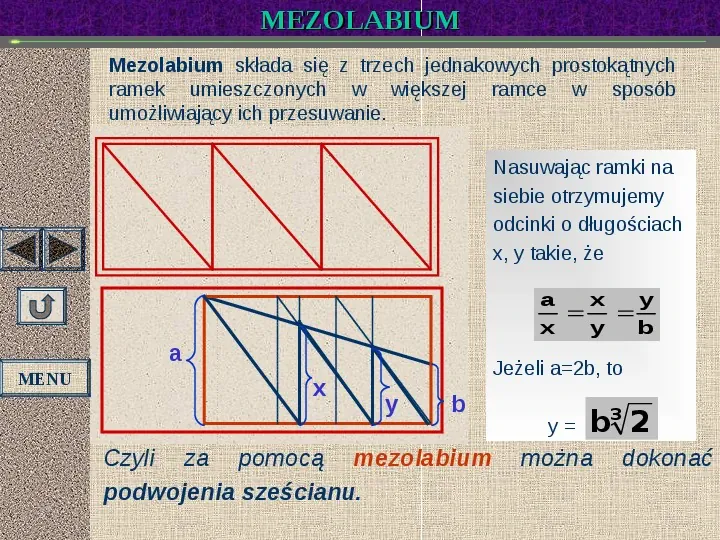
MEZOLABIUM Mezolabium składa się z trzech jednakowych prostokątnych ramek umieszczonych w większej ramce w sposób umożliwiający ich przesuwanie. Nasuwając ramki na siebie otrzymujemy odcinki o długościach x, y takie, że a x y x y b a MENU x Jeżeli a2b, to y b Czyli za pomocą mezolabium podwojenia sześcianu. y b3 2 można dokonać

Slide 10

TRYSEKCJA KĄTA Zadanie konstrukcyjne postawione przez matematyków starożytnej Grecji. Podzielić kąt na trzy równe części Trysekcja kąta jest konstrukcją niewykonalną dla nieskończenie wielu kątów. W każdym przedziale (a; b), 0 a b 2 istnieje taka liczba c, że trysekcja kąta o mierze równej c jest niewykonalna za pomocą cyrkla i linijki. Można wykonać trysekcję kąta o mierze równej k n , gdzie k jest dowolną liczbą naturalną, natomiast n i 3 są liczbami względnie pierwszymi [tzn. NWD(n,3)1]. Konsekwencją niewykonalności trysekcji kąta o mierze 3 jest np. niewykonalność konstrukcji dziewięciokąta foremnego. MENU

Slide 11

KWADRATURA KOŁA Kwadratura figury geometrycznej to zadanie konstrukcyjne polegające na konstrukcji metodą cyrkla i linijki kwadratu o polu równym polu danej figury geometrycznej. Kwadratura dowolnego wielokąta jest wykonalna. Aby ją przeprowadzić, wystarczy zauważyć, że: każdy wielokąt można przedstawić jako sumę skończonej liczby trójkątów o rozłącznych wnętrzach można przeprowadzić kwadraturę dowolnego trójkąta [zob. kwadratura trójkąta] można skonstruować kwadrat o polu równym sumie dwóch kwadratów Kwadratura koła jest konstrukcją niewykonalną, ponieważ liczba jest liczbą przestępną. Możliwe są jedynie konstrukcje kwadratów o polach bliskich polu danego koła. MENU

Slide 12

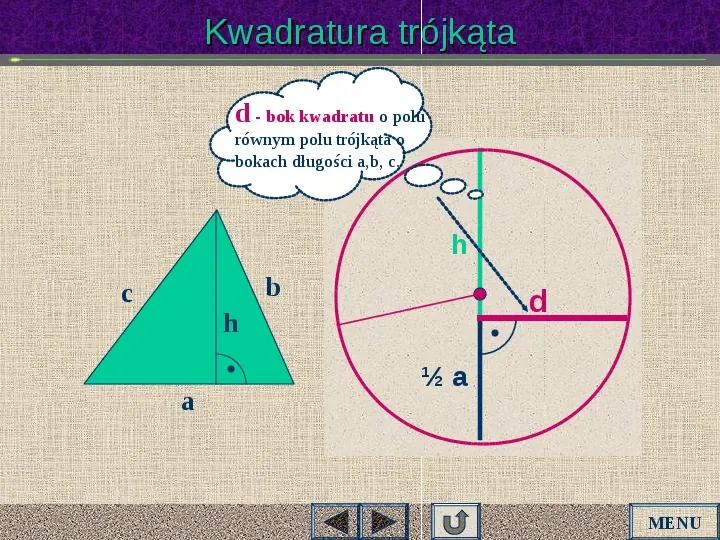
Kwadratura trójkąta d - bok kwadratu o polu równym polu trójkąta o bokach długości a,b, c. h b c d h a a MENU

Slide 13

KONSTRUKCJE Mohra-Mascheroniego Konstrukcje geometryczne wykonane za pomocą cyrkla (bez użycia linijki), tj. metodą umożliwiającą konstrukcję okręgu o danym środku i danym promieniu, znalezienie punktów przecięcia dwóch skonstruowanych okręgów i wybór dowolnego punktu na skonstruowanym okręgu. Uważa się przy tym, że prosta jest dana, jeżeli dane są jej dwa różne punkty. Matematyk wł. L. Mascheroni oraz wcześniej matematyk duń. G. Mohr udowodnili, że zadania konstrukcyjne polegające na wyznaczeniu punktu przecięcia dwóch prostych przechodzących przez dane punkty oraz na wyznaczeniu punktów przecięcia danego okręgu z prostą przechodzącą przez dane punkty można rozwiązać tylko za pomocą cyrkla. Tym samym każdą konstrukcję wykonalną przy użyciu cyrkla i linijki można przeprowadzić korzystając tylko z cyrkla. W praktyce okazuje się jednak, że dla większości konstrukcji jest to zadanie bardzo długie i żmudne. PRZYKŁAD konstrukcji Mohra-Mascheroniego MENU

Slide 14

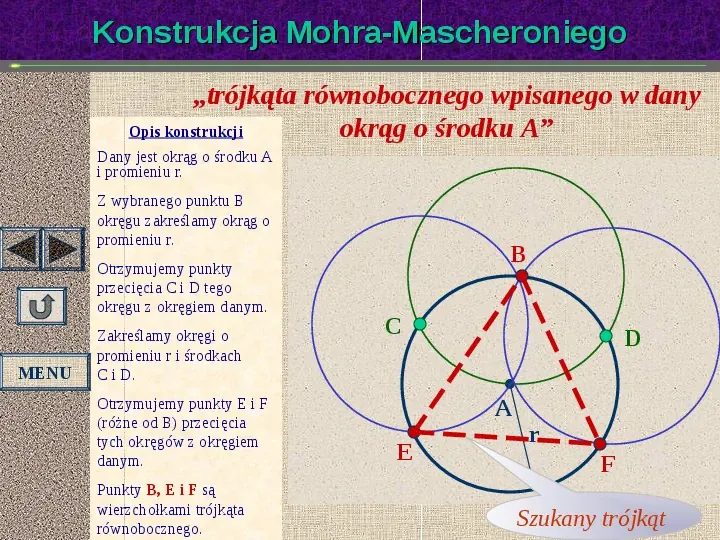
Konstrukcja Mohra-Mascheroniego trójkąta równobocznego wpisanego w dany Opis konstrukcji okrąg o środku A Dany jest okrąg o środku A i promieniu r. Z wybranego punktu B okręgu zakreślamy okrąg o promieniu r. Otrzymujemy punkty przecięcia C i D tego okręgu z okręgiem danym. MENU Zakreślamy okręgi o promieniu r i środkach C i D. Otrzymujemy punkty E i F (różne od B) przecięcia tych okręgów z okręgiem danym. Punkty B, E i F są wierzchołkami trójkąta równobocznego. B C D A E r F Szukany trójkąt

Slide 15

Konstrukcje elementarne Aby rozwiązania zadań konstrukcyjnych były czytelne, a opisy konstrukcji niezbyt długie , często posługujemy się konstrukcjami elementarnymi. Należą do nich m.in. Przykłady Symetralna odcinka Dwusieczna kąta Prosta prostopadła do danej prost ej przechodząca przez dany punkt Prosta równoległa do danej prostej w danej odległości od tej prostej Styczna do danego okręgu przecho dząca przez dany punkt leżący na zewnątrz okręgu MENU

Slide 16

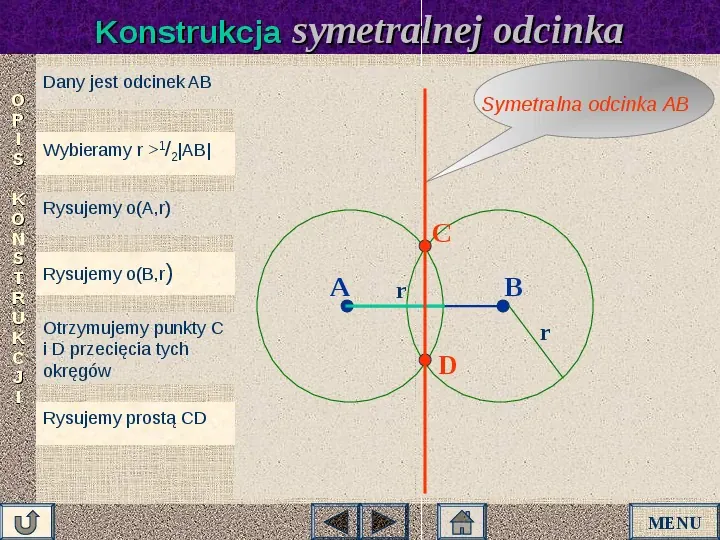
Konstrukcja symetralnej odcinka Dany jest odcinek AB O P I Wybieramy r 12AB S K O N S T R U K C J I Symetralna odcinka AB Rysujemy o(A,r) Rysujemy o(B,r) Otrzymujemy punkty C i D przecięcia tych okręgów C A B r r D Rysujemy prostą CD MENU

Slide 17

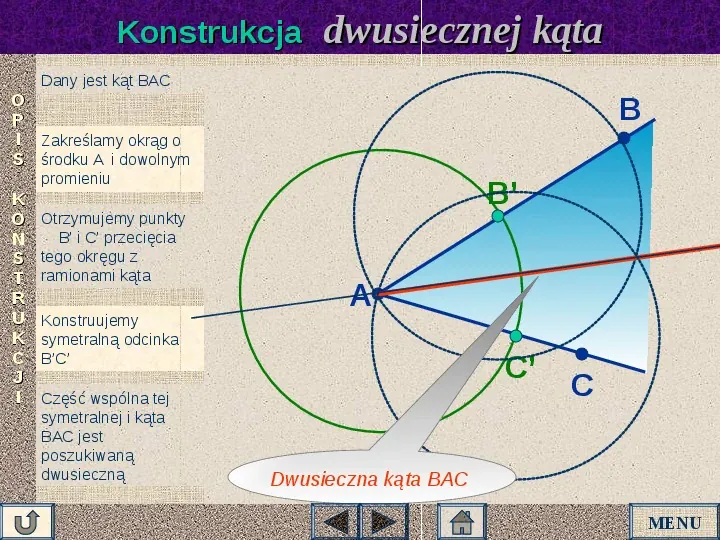
Konstrukcja dwusiecznej kąta Dany jest kąt BAC O P I Zakreślamy okrąg o S środku A i dowolnym B promieniu K O N S T R U K C J I Otrzymujemy punkty B i C przecięcia tego okręgu z ramionami kąta Konstruujemy symetralną odcinka BC Część wspólna tej symetralnej i kąta BAC jest poszukiwaną dwusieczną B A C C Dwusieczna kąta BAC MENU

Slide 18

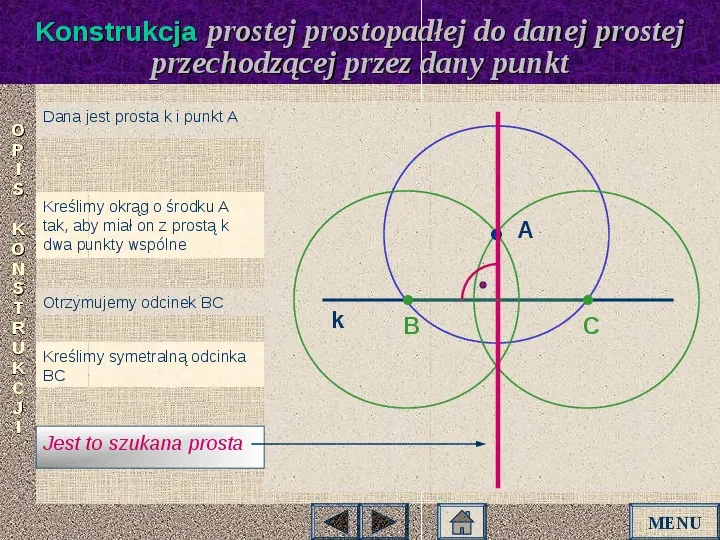
Konstrukcja prostej prostopadłej do danej prostej przechodzącej przez dany punkt O P I S Dana jest prosta k i punkt A Kreślimy okrąg o środku A tak, aby miał on z prostą k dwa punkty wspólne K O N S T Otrzymujemy odcinek BC R U Kreślimy symetralną odcinka K BC C J I A k B C Jest to szukana prosta MENU

Slide 19

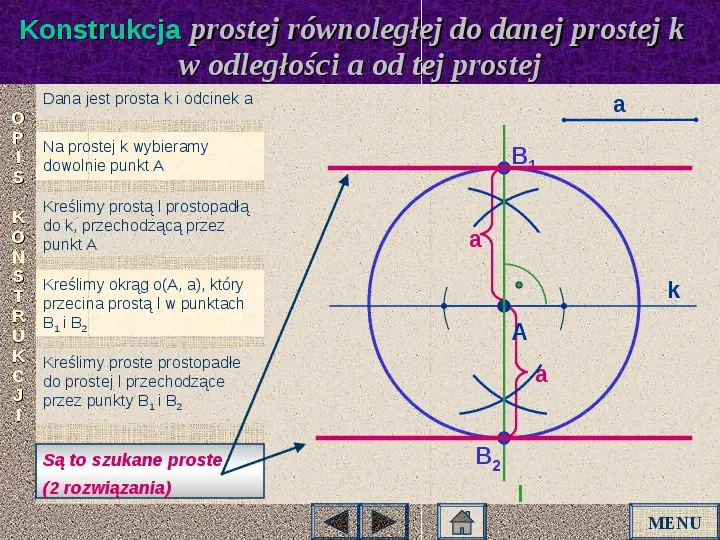
Konstrukcja prostej równoległej do danej prostej k w odległości a od tej prostej Dana jest prosta k i odcinek a a O P Na prostej k wybieramy I dowolnie punkt A S K O N S T R U K C J I Kreślimy prostą l prostopadłą do k, przechodzącą przez punkt A B1 a Kreślimy okrąg o(A, a), który przecina prostą l w punktach B1 i B2 k A Kreślimy proste prostopadłe do prostej l przechodzące przez punkty B1 i B2 Są to szukane proste (2 rozwiązania) a B2 l MENU

Slide 20

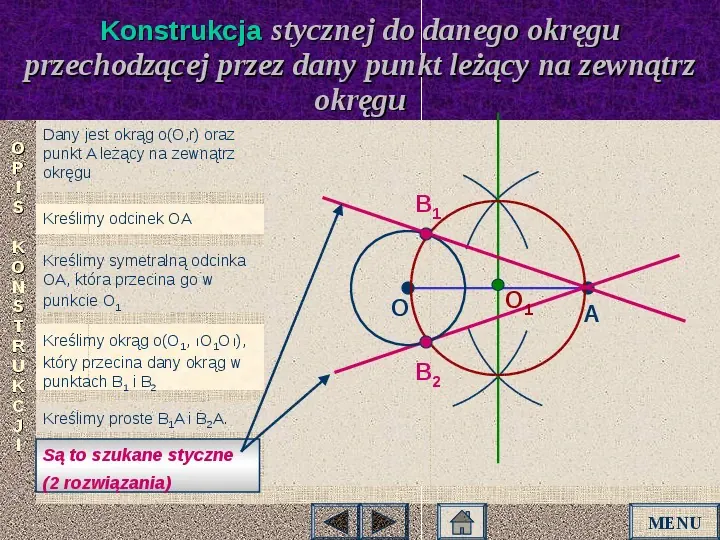
Konstrukcja stycznej do danego okręgu przechodzącej przez dany punkt leżący na zewnątrz okręgu O P I S K O N S T R U K C J I Dany jest okrąg o(O,r) oraz punkt A leżący na zewnątrz okręgu B1 Kreślimy odcinek OA Kreślimy symetralną odcinka OA, która przecina go w punkcie O1 Kreślimy okrąg o(O1, O1O), który przecina dany okrąg w punktach B1 i B2 O1 O A B2 Kreślimy proste B1A i B2A. Są to szukane styczne (2 rozwiązania) MENU

Slide 21

Wielokąty foremne Wielokąt foremny Jest to wielokąt, który ma wszystkie boki równej długości i wszystkie kąty równe. Własności: 1. Jest wielokątem wypukłym. 2. Na każdym wielokącie foremnym można opisać okrąg. W każdy wielokąt foremny można wpisać okrąg. Okręgi te są współśrodkowe. Przykłady: Trójkąt równoboczny konstrukcja Kwadrat konstrukcja Pięciokąt foremny konstrukcja Sześciokąt foremny 3. Symetralna boku jest jego osią symetrii. 4. Dwusieczna kąta zawiera się w jego osi symetrii. MENU konstrukcja

Slide 22

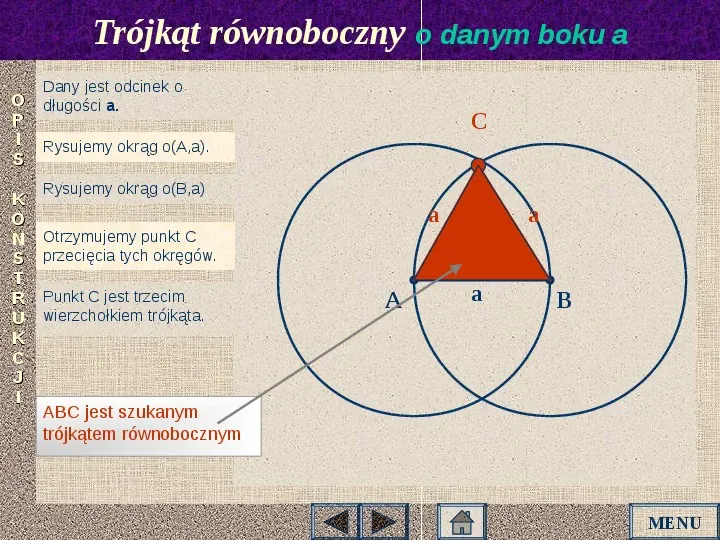
Trójkąt równoboczny o danym boku a Dany jest odcinek o długości a. O P I Rysujemy okrąg o(A,a). S K O N S T R U K C J I C Rysujemy okrąg o(B,a) a a Otrzymujemy punkt C przecięcia tych okręgów. Punkt C jest trzecim wierzchołkiem trójkąta. A a B ABC jest szukanym trójkątem równobocznym MENU

Slide 23

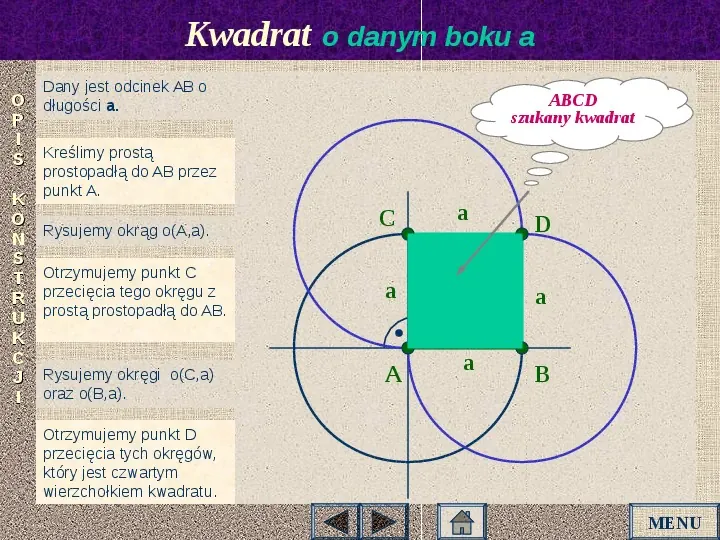
Kwadrat o danym boku a Dany jest odcinek AB o długości a. O P I S Kreślimy prostą K O N S T R U K C J I ABCD szukany kwadrat prostopadłą do AB przez punkt A. Rysujemy okrąg o(A,a). Otrzymujemy punkt C przecięcia tego okręgu z prostą prostopadłą do AB. Rysujemy okręgi o(C,a) oraz o(B,a). C a a A D a a B Otrzymujemy punkt D przecięcia tych okręgów, który jest czwartym wierzchołkiem kwadratu. MENU

Slide 24

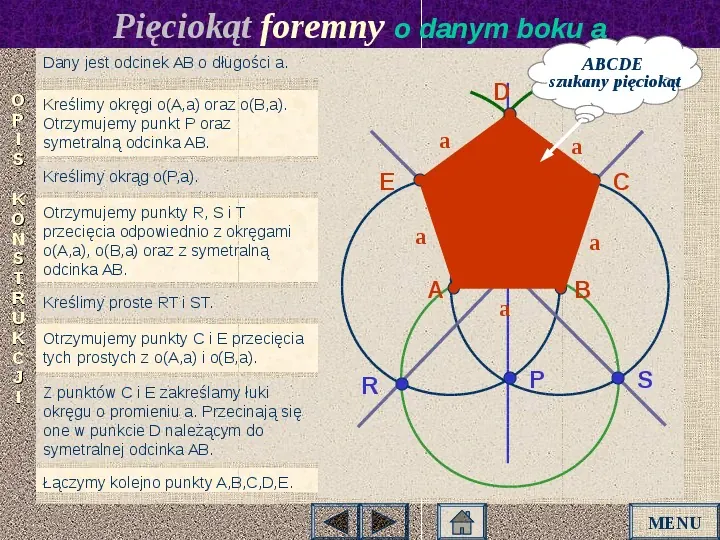
Pięciokąt foremny o danym boku a Dany jest odcinek AB o długości a. D O Kreślimy okręgi o(A,a) oraz o(B,a). P Otrzymujemy punkt P oraz I symetralną odcinka AB. S a Kreślimy okrąg o(P,a). K O N S T R U K C J I a E Otrzymujemy punkty R, S i T przecięcia odpowiednio z okręgami o(A,a), o(B,a) oraz z symetralną odcinka AB. C a Otrzymujemy punkty C i E przecięcia tych prostych z o(A,a) i o(B,a). R a T A Kreślimy proste RT i ST. Z punktów C i E zakreślamy łuki okręgu o promieniu a. Przecinają się one w punkcie D należącym do symetralnej odcinka AB. ABCDE szukany pięciokąt B a P S Łączymy kolejno punkty A,B,C,D,E. MENU

Slide 25

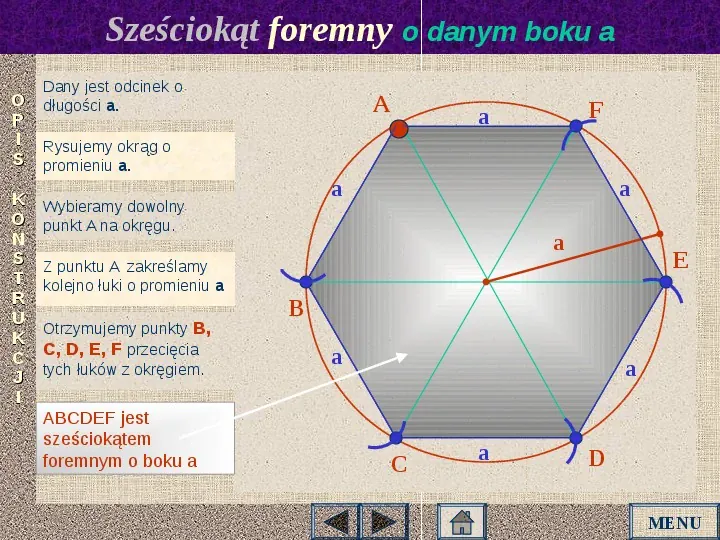
Sześciokąt foremny o danym boku a Dany jest odcinek o długości a. O P I Rysujemy okrąg o S promieniu a. K O N S T R U K C J I A F a a Wybieramy dowolny punkt A na okręgu. a a E Z punktu A zakreślamy kolejno łuki o promieniu a Otrzymujemy punkty B, C, D, E, F przecięcia tych łuków z okręgiem. ABCDEF jest sześciokątem foremnym o boku a B a a C a D MENU

Slide 26

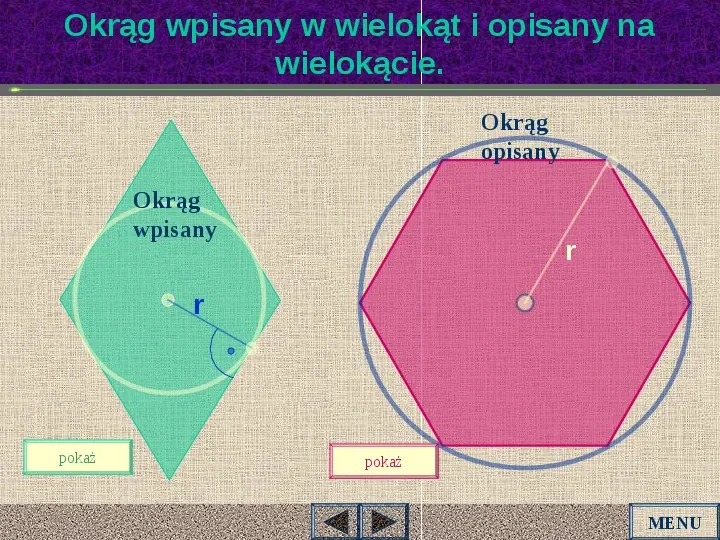
Okrąg wpisany w wielokąt i opisany na wielokącie. Okrąg opisany Okrąg wpisany r r pokaż pokaż MENU

Slide 27

Okrąg wpisany w wielokąt. Definicja: Twierdzenie: można opisać na okręgu (okrąg można Jeżeli każdy bok Wielokąt wpisać w wielokąt) wtedy i tylko wtedy, gdy wielokąta jest dwusieczne kątów wewnętrznych tego wielokąta przecinają się w jednym punkcie. Ten punkt jest styczny do środkiem okręgu wpisanego w wielokąt. okręgu, to wielokąt jest W dowolny trójkąt można wpisać okrąg. opisany na konstrukcja okręgu, a okrąg nazywa się Okrąg można wpisać w czworokąt okręgiem wtedy i tylko wtedy, gdy sumy długości wpisanym w przeciwległych boków czworokąta są równe. wielokąt. konstrukcja MENU

Slide 28

Okrąg opisany na wielokącie. Definicja: Definicja Twierdzenie: Wielokąt można wpisać w okrąg (okrąg można opisać na wielokącie) wtedy i tylko wtedy, gdy symetralne boków tego wielokąta przecinają się w jednym punkcie. Ten punkt jest środkiem okręgu opisanego na wielokącie. Wielokąt, którego wszystkie wierzchołki należą do pewnego okręgu, Na dowolnym trójkącie można opisać nazywa się okrąg. wielokątem konstrukcja wpisanym w okrąg , okrąg zaś- Okrąg można opisać na czworokącie okręgiem wtedy i tylko wtedy, gdy sumy kątów czworokąta są opisanym na przeciwległych równe (i wynoszą 180). konstrukcja wielokącie. MENU

Slide 29

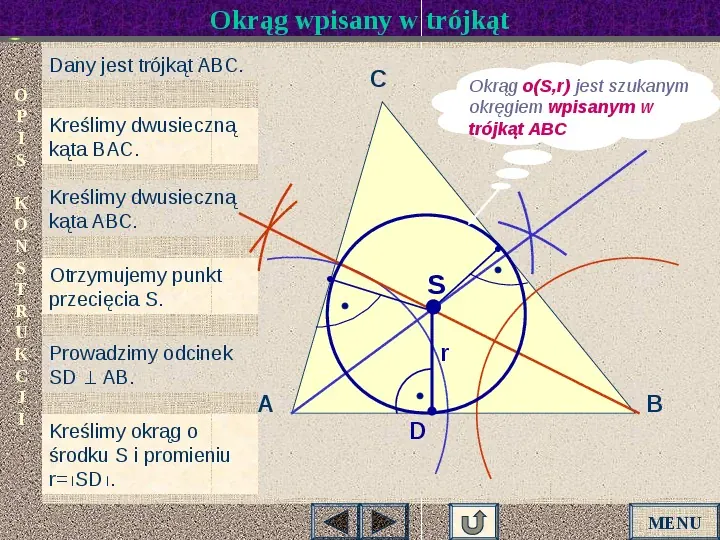
Okrąg wpisany w trójkąt Dany jest trójkąt ABC. O P I S K O N S T R U K C J I C Okrąg o(S,r) jest szukanym okręgiem wpisanym w trójkąt ABC Kreślimy dwusieczną kąta BAC. Kreślimy dwusieczną kąta ABC. Otrzymujemy punkt przecięcia S. S r Prowadzimy odcinek SD AB. A Kreślimy okrąg o środku S i promieniu rSD. D B MENU

Slide 30

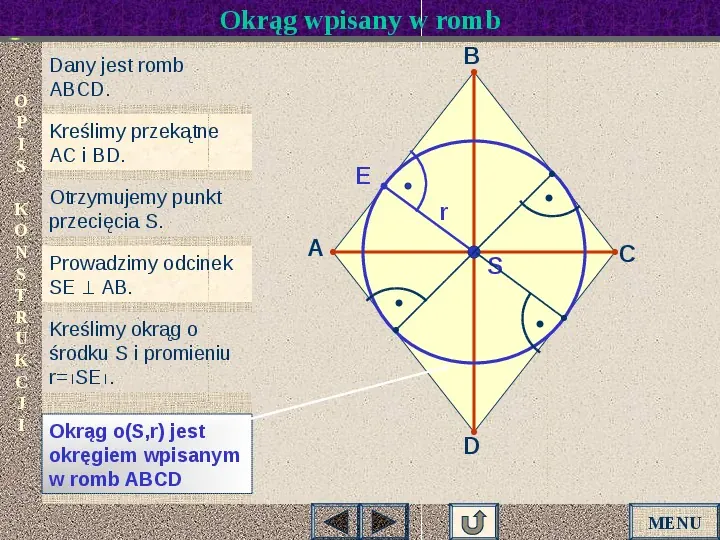
Okrąg wpisany w romb O P I S K O N S T R U K C J I B Dany jest romb ABCD. Kreślimy przekątne AC i BD. E Otrzymujemy punkt przecięcia S. Prowadzimy odcinek SE AB. r A S C Kreślimy okrąg o środku S i promieniu rSE. Okrąg o(S,r) jest okręgiem wpisanym w romb ABCD D MENU

Slide 31

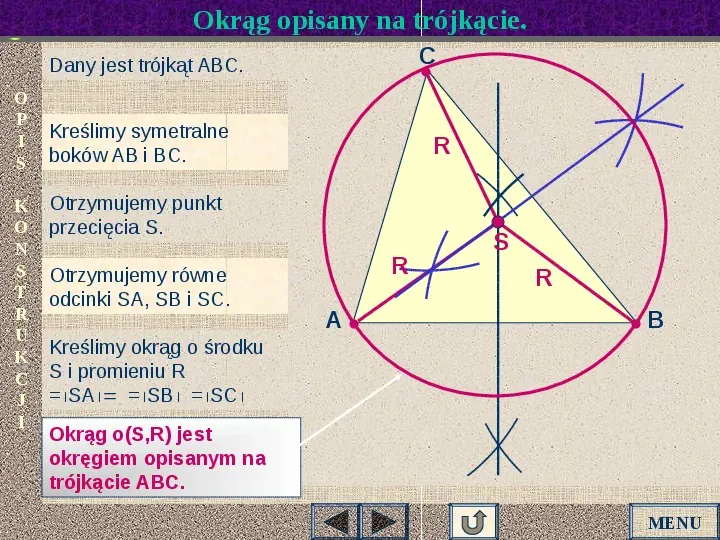
Okrąg opisany na trójkącie. C Dany jest trójkąt ABC. O P I S K O N S T R U K C J I Kreślimy symetralne boków AB i BC. R Otrzymujemy punkt przecięcia S. Otrzymujemy równe odcinki SA, SB i SC. R A S R B Kreślimy okrąg o środku S i promieniu R SASBSC Okrąg o(S,R) jest okręgiem opisanym na trójkącie ABC. MENU

Slide 32

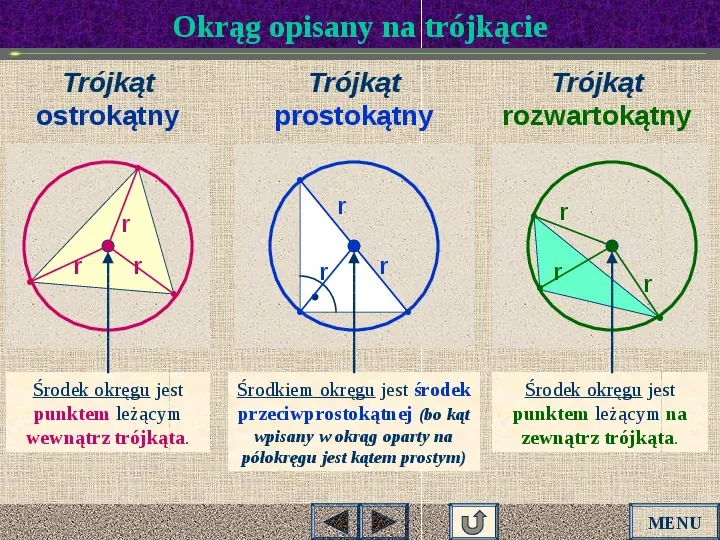
Okrąg opisany na trójkącie Trójkąt ostrokątny Trójkąt prostokątny r r r r Środek okręgu jest punktem leżącym wewnątrz trójkąta. r Trójkąt rozwartokątny r r Środkiem okręgu jest środek przeciwprostokątnej (bo kąt wpisany w okrąg oparty na półokręgu jest kątem prostym) r r Środek okręgu jest punktem leżącym na zewnątrz trójkąta. MENU

Slide 33

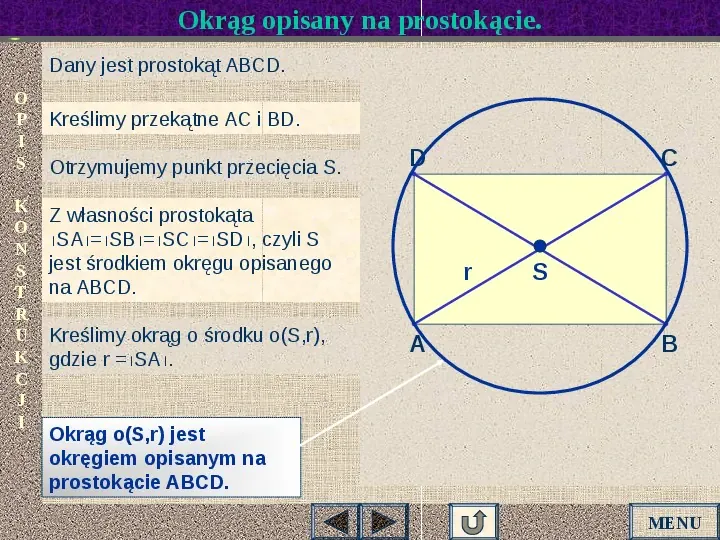
Okrąg opisany na prostokącie. Dany jest prostokąt ABCD. O P I S K O N S T R U K C J I Kreślimy przekątne AC i BD. Otrzymujemy punkt przecięcia S. D Z własności prostokąta SASBSCSD, czyli S jest środkiem okręgu opisanego na ABCD. Kreślimy okrąg o środku o(S,r), gdzie r SA. C Ar A A ASA A A A A B Okrąg o(S,r) jest okręgiem opisanym na prostokącie ABCD. MENU

Slide 34

Tw. Pitagorasa, Talesa i jednokładność zastosowanie w wykonywaniu konstrukcji. Twierdzenie Pitagorasa Twierdzenie Talesa Jednokładność i jej własności MENU

Slide 35

Twierdzenie Pitagorasa: Jeżeli trójkąt jest prostokątny, to suma kwadratów długości przyprostokątnych jest równa kwadratowi długości przeciwprostokątnej. ZAŁ. b c TEZA: 2 2 a b c 2 a a, b długości przyprostokątnych c długość przeciwprostokątnej Zastosowanie MENU

Slide 36

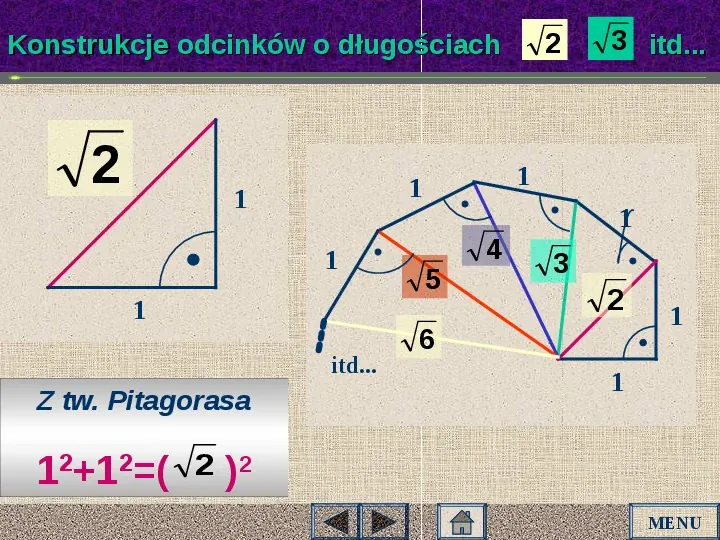
2, Konstrukcje odcinków o długościach 2 1 1 itd... Z tw. Pitagorasa 2 2 1 1 ( 2 1 1 1 3 itd... 5 4 1 3 2 6 1 1 )2 MENU

Slide 37

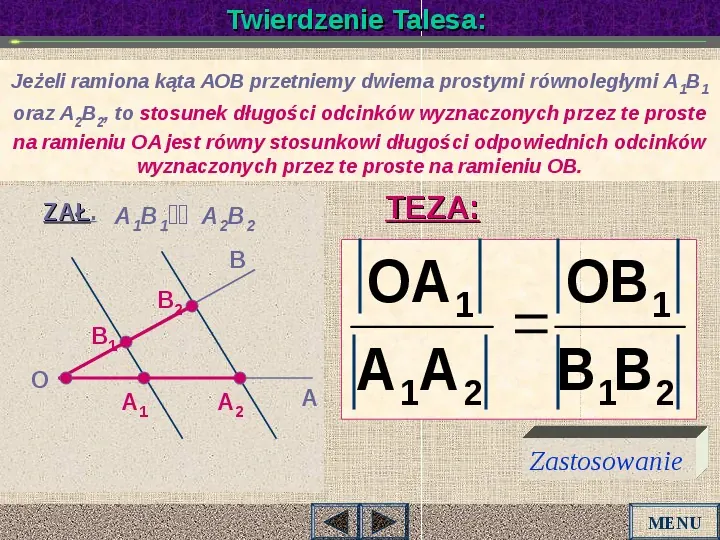
Twierdzenie Talesa: Jeżeli ramiona kąta AOB przetniemy dwiema prostymi równoległymi A 1B1 oraz A2B2, to stosunek długości odcinków wyznaczonych przez te proste na ramieniu OA jest równy stosunkowi długości odpowiednich odcinków wyznaczonych przez te proste na ramieniu OB. TEZA: ZAŁ. ZAŁ A1B1A2B2 B B2 B1 O A1 A2 A OA 1 OB 1 A 1A 2 B1B 2 Zastosowanie MENU

Slide 38

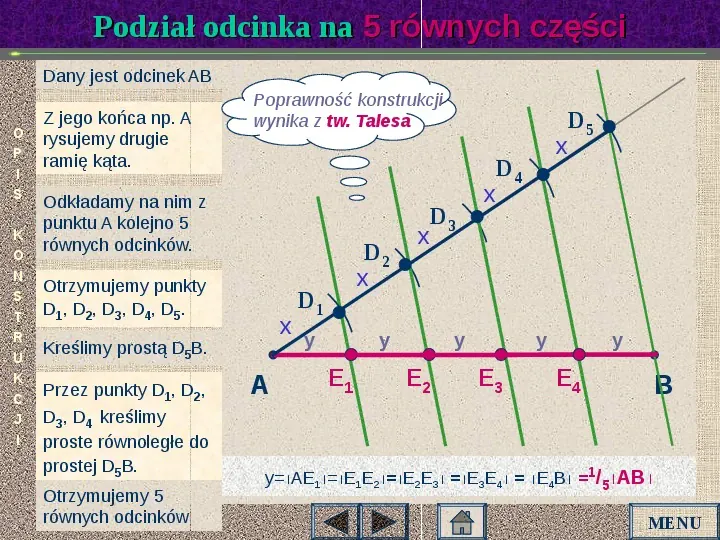
Podział odcinka na 5 równych części Dany jest odcinek AB O P I S K O N S T R U K C J I Z jego końca np. A rysujemy drugie ramię kąta. Poprawność konstrukcji wynika z tw. Talesa Odkładamy na nim z punktu A kolejno 5 równych odcinków. D3 Otrzymujemy punkty D1, D2, D3, D4, D5. x Kreślimy prostą D5B. Przez punkty D1, D2, D3, D4 kreślimy proste równoległe do prostej D5B. Otrzymujemy 5 równych odcinków D5 A D2 x D1 y D4 x x y E1 x y E2 y y E3 E4 B yAE1E1E2E2E3 E3E4 E4B 15AB MENU

Slide 39

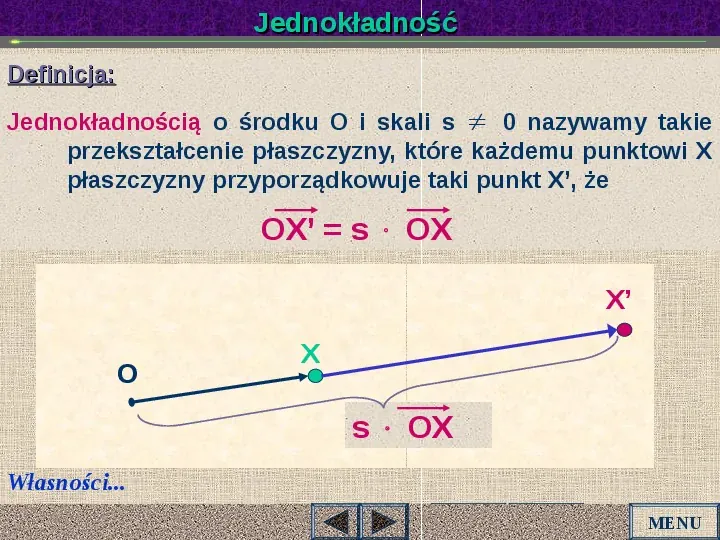
Jednokładność Definicja: Jednokładnością o środku O i skali s 0 nazywamy takie przekształcenie płaszczyzny, które każdemu punktowi X płaszczyzny przyporządkowuje taki punkt X, że OX s OX X O X s OX Własności... MENU

Slide 40

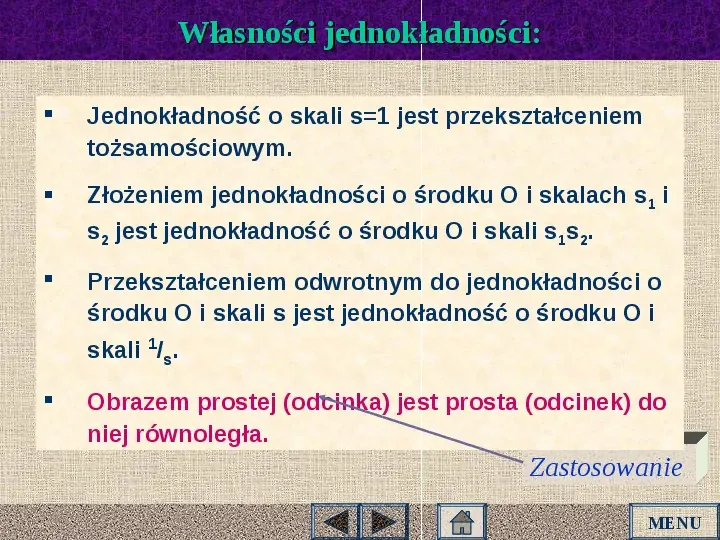
Własności jednokładności: Jednokładność o skali s1 jest przekształceniem tożsamościowym. Złożeniem jednokładności o środku O i skalach s1 i s2 jest jednokładność o środku O i skali s1s2. Przekształceniem odwrotnym do jednokładności o środku O i skali s jest jednokładność o środku O i skali 1s. Obrazem prostej (odcinka) jest prosta (odcinek) do niej równoległa. Zastosowanie MENU

Slide 41

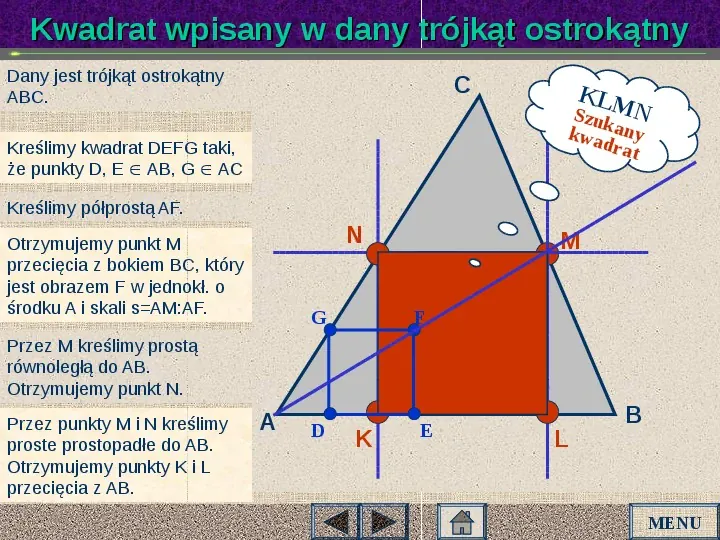
Kwadrat wpisany w dany trójkąt ostrokątny Dany jest trójkąt ostrokątny ABC. C KLM N S zuka kwa ny drat Kreślimy kwadrat DEFG taki, że punkty D, E AB, G AC Kreślimy półprostą AF. N Otrzymujemy punkt M przecięcia z bokiem BC, który jest obrazem F w jednokł. o środku A i skali sAM:AF. G M F Przez M kreślimy prostą równoległą do AB. Otrzymujemy punkt N. Przez punkty M i N kreślimy proste prostopadłe do AB. Otrzymujemy punkty K i L przecięcia z AB. A D K E L B MENU

Slide 42

ZADANIE KONSTRUKCYJNE 1) Etapy rozwiązania zadania konst rukcyjnego. 2) Jak rozwiązywać zadania konstru kcyjne ? (przykłady) MENU

Slide 43

Etapy rozwiązania: Analiza zadania szkicujemy rysunek tak, jakby zadanie było rozwiązane, zaznaczamy elementy dane i szukane; określamy, jak od danych przejść do szukanych. Konstrukcja i jej opis konstruujemy szukaną figurę (używając jedynie cyrkla i linijki) i opisujemy czynności, które wykonujemy. Dowód poprawności konstrukcji wykazujemy, że uzyskane przez nas rozwiązanie spełnia warunki zadania. Dyskusja istnienia i liczby rozwiązań ustalamy warunki zadania, dla których istnieje rozwiązanie oraz stwierdzamy, czy istnieje jedno rozwiązanie, czy też może być ich więcej. MENU

Slide 44

PRZYKŁADY ZADAŃ ZADANIE 1: Skonstruuj trójkąt ABC mając dane: sumę boków AB BC, kąt ABC i wysokość CD; ZADANIE 2: Dany jest okrąg o(A, R) i prosta k. Skonstruuj okrąg o danym promieniu r styczny zewnętrznie do okręgu o(A, R) i styczny do prostej k; MENU

Slide 45

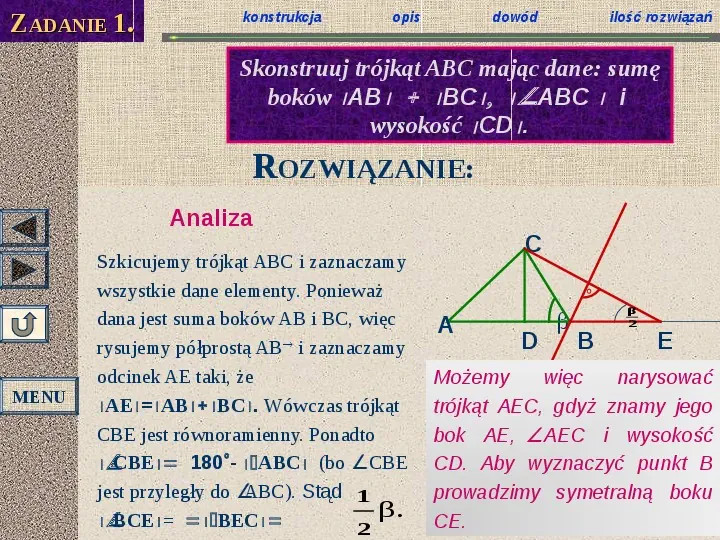
ZADANIE 1. konstrukcja opis dowód ilość rozwiązań Skonstruuj trójkąt ABC mając dane: sumę boków AB BCABC i wysokość CD . ROZWIĄZANIE: Analiza MENU Szkicujemy trójkąt ABC i zaznaczamy wszystkie dane elementy. Ponieważ dana jest suma boków AB i BC, więc rysujemy półprostą ABi zaznaczamy odcinek AE taki, że AEABBC. Wówczas trójkąt CBE jest równoramienny. Ponadto CBE180- ABC(bo CBE jest przyległy do ABC). Stąd 1 β. BCEBEC 2 C A D B β 2 E Możemy więc narysować trójkąt AEC, gdyż znamy jego bok AE,AEC i wysokość CD. Aby wyznaczyć punkt B prowadzimy symetralną boku CE.

Slide 46

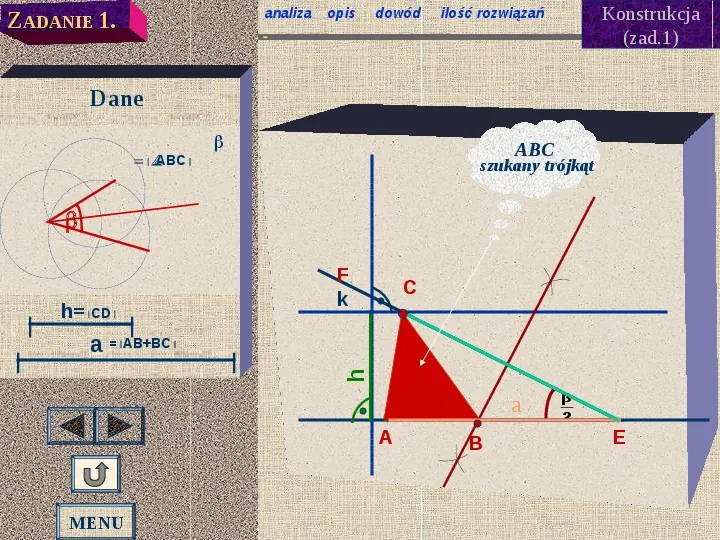
analiza ZADANIE 1. opis dowód Konstrukcja (zad.1) ilość rozwiązań Dane ABC ABC szukany trójkąt hCD F k C h a ABBC a A MENU B β 2 E

Slide 47

Opis konstrukcji (zad. 1). analiza konstrukcja dowód ilość rozwiązań Rysujemy prostą, wybieramy na niej dowolny punkt A i odkładamy odcinek AEa Konstruujemy kąt o mierze β i odkładamy go tak, aby jego wierzchołkiem był punkt E 2i jedno ramię zawierało się w półprostej EA. Drugie ramię oznaczamy EF Prowadzimy prostą k równoległą do prostej AE w odległości h od tej prostej. Przecina ona półprostą EF w punkcie C. MENU Konstruujemy symetralną odcinka EC, która przecina AE w punkcie B. ABC jest szukanym trójkątem. odcinek

Slide 48

Dowód poprawności konstrukcji (zad. 1). analiza konstrukcja opis ilość rozwiązań Punkt B należy do symetralnej odcinka CE, zatem BCBEiABBCABBEa. Trójkąt BEC jest β równoramienny i z konstrukcji wynika, że CEB . Stąd 2 CBE 180 - . Kąty CBE i CBA są przyległe, więc CBA 180 - (180 - ) ABC. Ponadto z konstrukcji wynika, że punkt C leży na prostej równoległej do prostej AE, odległej o MENU h od prostej AE, więc wysokość CD ma daną długość h.

Slide 49

Istnienie i liczba rozwiązań (zad. 1). analiza konstrukcja opis dowód 1 lub 0 Warunkiem dostatecznym istnienia rozwiązania jest, aby 0 ABC 180 oraz by symetralna MENU odcinka CE przecięła bok AE. W takim przypadku jest jedno rozwiązanie zadania; w przeciwnym wypadku brak rozwiązań.

Slide 50

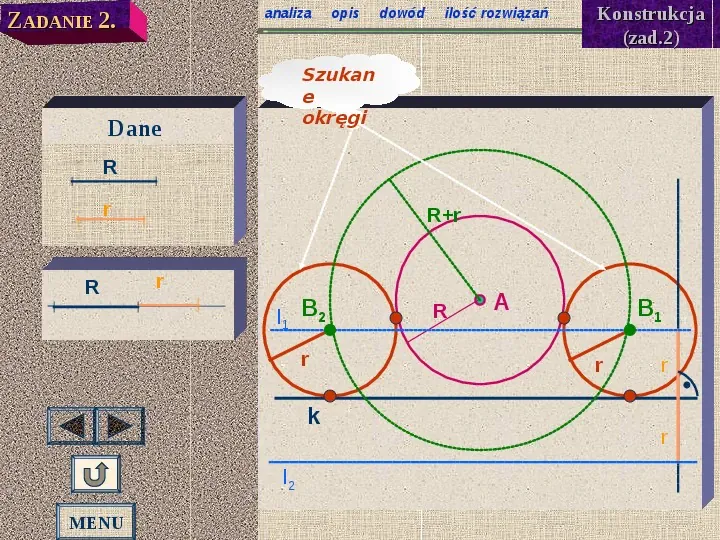
ZADANIE 2. konstrukcja opis dowód ilość rozwiązań Dany jest okrąg o(A,R) i prosta k. Skonstruuj okrąg o danym promieniu r styczny zewnętrznie do okręgu o(A, R) i styczny do prostej k. ROZWIĄZANIE: Analiza MENU Aby narysować szukany okrąg, należy wyznaczyć punkt B, który jest jego środkiem. Ponieważ okrąg dany i szukany mają być styczne zewnętrznie, więc odległość ich środków ma być równa sumie ich promieni (ABRr). Punkt B jest więc punktem okręgu o(A, Rr). Z drugiej strony szukany okrąg ma być styczny do prostej k, więc jego środek (punkt B) leży w odległości r od prostej k tzn. d(B, k)r. A R r B k

Slide 51

analiza ZADANIE 2. opis dowód ilość rozwiązań Konstrukcja (zad.2) Szukan e okręgi Dane R r R Rr r l1 B2 r k l2 MENU R A B1 r r r

Slide 52

Opis konstrukcji (zad. 2). konstrukcja analiza dowód ilość rozwiązań Budujemy odcinek o długości Rr. Zakreślamy okrąg o(A, Rr). Kreślimy proste l , l równoległe do prostej k w 1 2 odległości r od tej prostej. Otrzymujemy MENU punkty B1 i B2 przecięcia prostych z okręgiem o (A, Rr). tych Kreślimy okręgi o(B , r) i o(B , r). 1 2 Okręgi o(B1, r) i o(B2, r) spełniają warunki zadania.

Slide 53

Dowód poprawności konstrukcji (zad. 2). Konstrukcja opis analiza ilość rozwiązań Z konstrukcji wynika, że odległość punktów B1 i B2 od punktu A jest równa Rr, zatem okręgi o(B1,r) i o(B2,r) są styczne zewnętrznie MENU z okręgiem o(A,r). Punkty B1 i B2 leżą na prostej l1 takiej, że d(l1,k) r, więc zbudowane okręgi są styczne do prostej k.

Slide 54

Istnienie i liczba rozwiązań (zad. 2). konstrukcja opis dowód analiza 0,1,2,3,4 Zadanie ma tyle rozwiązań, ile jest punktów wspólnych sumy prostych l1 i l2 z okręgiem o(A, Rr). Oprócz otrzymanych dwóch rozwiązań mamy jeszcze następujące przypadki: MENU Brak rozwiązań Jedno rozwiązanie Trzy rozwiązania Cztery rozwiązania

Slide 55

Brak rozwiązań konstrukcja opis dowód Suma prostych l1 i l2 nie analiza ma punktów wspólnych z okręgiem o(A, 0 Rr) Rr R A l1 MENU k r r l2

Slide 56

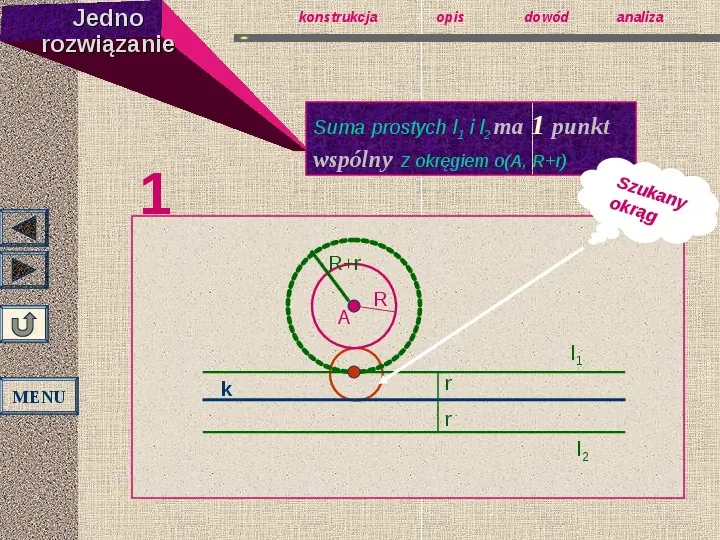
Jedno rozwiązanie konstrukcja opis Suma prostych l1 i l2 ma dowód analiza 1 punkt wspólny z okręgiem o(A, Rr) 1 Szu k okrą any g Rr A R l1 MENU k r r l2

Slide 57

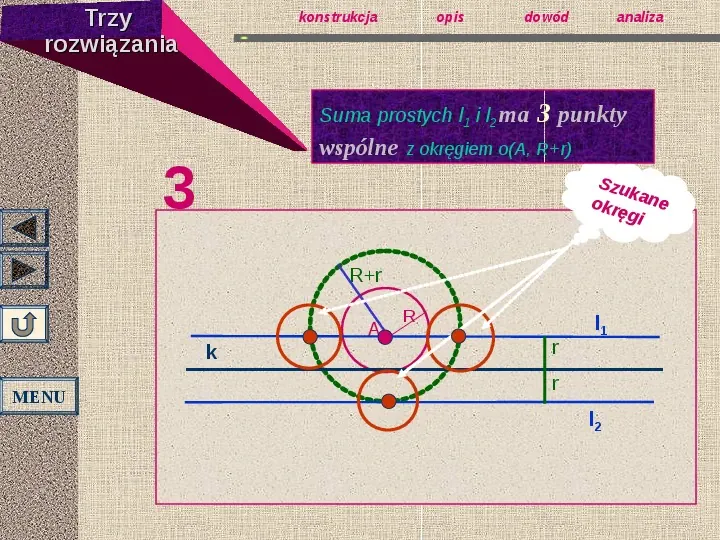
Trzy rozwiązania konstrukcja opis dowód Suma prostych l1 i l2 ma analiza 3 punkty wspólne z okręgiem o(A, Rr) 3 Szu k okrę ane gi Rr A k MENU R r l1 r l2

Slide 58

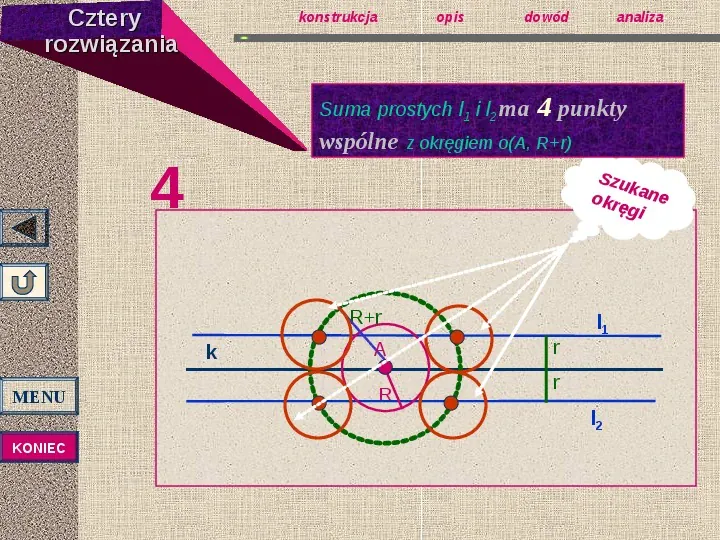
Cztery rozwiązania konstrukcja opis dowód Suma prostych l1 i l2 ma 4 punkty wspólne z okręgiem o(A, Rr) 4 Szu k okrę ane gi Rr k MENU KONIEC analiza A R r l1 r l2