Praktyczne wykorzystanie Twierdzenia Talesa

Zobacz slidy

Treść prezentacji

Slide 1

Praktyczne wykorzystanie Twierdzenia Talesa

Slide 2

Tales z Miletu Tales urodził się w Milecie, stolicy starożytnej greckiej prowincji Jonia, położonej na zachodnim wybrzeżu Azji Mniejszej, na terytorium należącym współcześnie do Turcji, około 620 r. p.n.e. Uważa się go za pierwszego z siedmiu mędrców, czyli uczonych mężów żyjących na przełomie VI i VI wieku przed narodzeniem Chrystusa. Lista siedmiu mędrców różniła się w zależności od miejsca, ale każdy z nich cieszył się wielkim uznaniem w swym rodzinnym mieście i zapamiętany był dzięki charakterystycznej maksymie. Ta, przypisywana Talesowi, brzmiała: Nadmierna pewność siebie prowadzi do klęski. Tales zmarł, jak się przypuszcza, około roku 540 p.n.e. Niektórzy historycy nauki uważają Talesa z Miletu za postać mityczną, podobnie jak Jazona, Perseusza czy innych herosów; postać Talesa symbolizuje okoliczności, w jakich tworzono podstawy ówczesnej wiedzy i filozofii i jest traktowania jako spersonifikowany nośnik pewnych idei.

Slide 3

Tales z Miletu KOSMOLOGIA Poglądy kosmologiczne głoszone przez Talesa znane są w głównej mierze dzięki przekazom Arystotelesa. Idea propagowana przez Talesa, jakoby wszystko, co istnieje, pochodziło z wody, występowała także w mitologii starożytnych Egipcjan i Babilończyków, jak również w poezji epickiej, której autorstwo przypisywano Homerowi. Tales próbował wytłumaczyć zjawiska zachodzące w świecie przyrody odwołując się do samej przyrody a nie do ingerencji bogów; dla przykładu był przekonany, że wszelkie trzęsienia ziemi biorą się właśnie stąd, że unosi się ona na powierzchni wody.

Slide 4

Tales z Miletu ASTRONOMIA W wieku XIX wykazano, że całkowite zaćmienie Słońca, które zostało przepowiedziane przez Talesa, miało faktycznie miejsce 28 maja 585 r. p.n.e. Doprowadziło ono wówczas do zaprzestania bitwy między armiami Lidii (krainy znajdującej się obecnie w zachodniej części Azji Mniejszej) i Medii (krainy wchodzącej obecnie w skład terytorium północno-zachodniego Iranu). Przepowiednia ta przyczyniła się do wzmocnienia reputacji Talesa jako astronoma. Jednakże dzisiaj sądzi się, że Tales nie posiadał odpowiedniej wiedzy, by określić dokładnie rozmiary cienia Księżyca oraz miejsca, w którym ten cień będzie padał.

Slide 5

Tales z Miletu GEOMETRIA Talesa uważa się powszechnie za twórcę abstrakcyjnej geometrii w jej czysto dedukcyjnej postaci, jaką rozwinąć miał później Euklides. Wprowadzone przez niego metody dedukcyjne stanowiły wielki postęp w stosunku do przybliżonych uogólnień podawanych przez uczonych egipskich czy babilońskich. Mówi się, że Tales wykorzystał swą wiedzę geometryczną do podawania odległości od brzegu, w jakiej znajdował się statek płynący po morzu oraz do obliczania wysokości piramid w Egipcie.

Slide 6

Twierdzenia geometryczne Talesa Zgodnie z przekazami starożytnych, a w szczególności greckiego filozofa Proklosa, działającego w V w. p.n.e., Talesowi przypisuje się następujące twierdzenia geometryczne: 1. Średnica dzieli okrąg na połowy. 2. Dwa kąty przy podstawie trójkąta równoramiennego są równe. 3. Kąty wierzchołkowe, czyli kąty naprzeciw siebie, powstałe na skutek przecięcia dwóch linii prostych, są równe. 4. Kąt wpisany w okrąg i oparty na jego średnicy jest kątem prostym. 5. Jeżeli w dwóch trójkątach bok i przyległe do niego kąty są równe, to te trójkąty są przystające.

Slide 7

Twierdzenie Talesa Jeżeli ramiona kąta lub ich przedłużenia przetniemy dwiema prostymi równoległymi, to długości odcinków, w wyznaczonych przez te proste na jednym ramieniu kąta lub jego przedłużeniu, są proporcjonalne do długości odpowiednich odcinków wyznaczonych przez te proste, na drugim ramieniu kąta lub na jego przedłużeniu. TWIERDZENIE ODWROTNE DO TWIERDZENIA TALESA Jeżeli ramiona kąta lub ich przedłużenie przetniemy dwiema prostymi i długości odcinków wyznaczonych przez te proste na jednym ramieniu kąta lub jego przedłużeniu są proporcjonalne do długości odpowiednich odcinków na drugim ramieniu kata lub jego przedłużeniu, to te proste są równoległe.

Slide 8

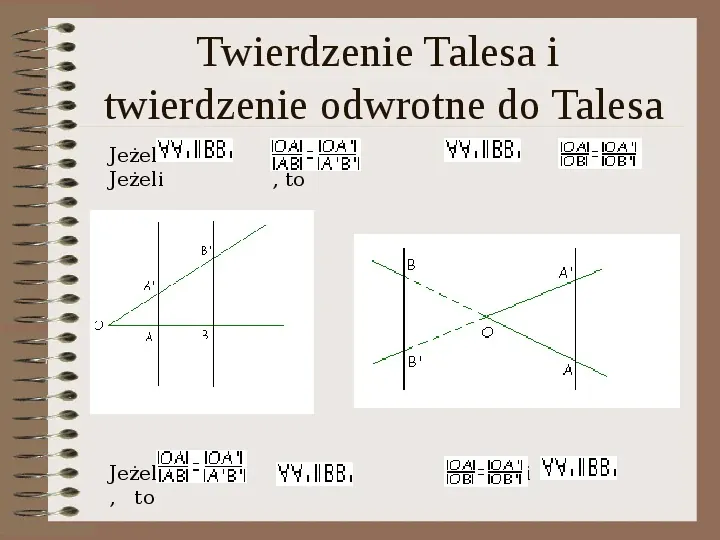
Twierdzenie Talesa i twierdzenie odwrotne do Talesa Jeżeli Jeżeli Jeżeli , to , to , to , to Jeżeli

Slide 9

ZADANIA Zadanie 1 Z odległości 5 m wykonano zdjęcie człowieka mającego 170 cm wzrostu, aparatem, którego długość obiektywu w chwili wykonania zdjęcia była równa 0,1 m. Oblicz, jaką wysokość ma obraz tego człowieka na AB wysokość osoby fotografii. AB wysokość obrazu tej osoby na fotografii Odp. Obraz człowieka na fotografii ma wysokość 3,4 cm

Slide 10

Zadanie 2 Jacek i Wacek stoją na przeciwnych brzegach rzeki. Korzystając z danych na rysunku, oblicz szerokość rzeki. 5m x 8m 20 m 100 m 8 x : 8 x 12,5 m szerokość rzeki Odp. Rzeka ma szerokość 12,5 m.

Slide 11

Zadanie 3 danych rysunku. Oblicz wysokość drzewa na podstawie zamieszczonych na 36 m x 12 m 2m 12 x 72 m x 6 m wysokość korony drzewa 6 2 8 m wysokość drzewa Odp. Drzewo ma 8 m wysokości.

Slide 12

Zadanie 4 Oblicz szerokość rzeki na podstawie danych zamieszczonych na rysunku 3,2 m 2 m x30 m 2 x 96 m x 48 m szerokość rzeki Odp. Szerokość rzeki wynosi 48 m.

Slide 13

Tales z Miletu będąc już w podeszłym wieku wybrał się do Egiptu, gdzie zadziwił wszystkich metodą mierzenia wysokości piramid za pomocą długości cienia. Zadanie 5 Oblicz wysokość piramidy Cheopsa, mając dane : długość krawędzi podstawy 230 m, długość cienia piramidy 250 m, długość użytego drąga 3 m, długość cienia drąga 7 m 0,5 230 m 250 m 365 m długość połowy podstawy i 3m cienia 7 m x365 m 1095 7 x :7 x 156,43 m Odp. Piramida Cheopsa ma wysokość 156,43 m.

Slide 14

Zadanie 6 Dom o szerokości 15 m sfotografowano aparatem, którego odległość soczewki od błony fotograficznej jest równa 8 cm. Oblicz odległość aparatu od domu, jeżeli szerokość domu na zdjęciu jest równa 10 cm. x 1500 8 10 12000 10 x x 1200 cm 12 m Odp. Odległość aparatu od domu wynosi 12 m.

Slide 15

Zadanie 7 W skansenie żuraw studzienny. Jego dźwignię AB podparto w punkcie C tak, że ramiona dźwigni mają długości: AC 2,4 i CB 7,2 m. O ile metrów opuści się koniec dźwigni B, gdy koniec A podniesie się na wysokość 4 metrów. 7,2 m 2,4 m x4 m 28, 8 2,4x: 2,4 x 12m Odp. Koniec dźwigni B opuści się o 12 m.

Slide 16

Zadanie 8 Maszt wysok0ości 5 m rzuca cień długości 7,5 m. W tym samym czasie w tej samej miejscowości pewien budynek rzuca cień długości 36 m. Jaką wysokość ma ten budynek. 36 m 5 m7,5 m X 2,5 x 180 X 24 m Odp. Budynek ma wysokość 24 m.

Slide 17

Zadanie 9 Zwiń kartkę papieru w rurkę. Jakiej wielkości przedmioty można obejrzeć przez tę rurkę z odległości 100 metrów, jeżeli rurka ma długość 20 cm , a średnicę 2 cm? 100 m x 0,2 m 0,02 m 0,2 2 : 0,2 x 10 m Odp. Wielkość przedmiotów z odległości 100 m wynosi 10 m.

Slide 18

Zadanie 10 Drabina o długości 2,5 m po oparciu o ścianę domu sięga na wysokość 2 m. a) Jak wysoko sięga drabina o długości 3,5 m, jeśli jest ustawiona pod tym samym kątem? 2,5 m 2 m 3,5 m x 2,5 x 7 m : 2,5 x 2,8 m Odp. Drabina sięga na wysokość 2,8 m.

Slide 19

b) Jaką długość ma drabina, jeśli ustawiona pod tym samym kątem sięga na wysokość 1,8 m? 2,5 m 2m x1,8 m 4,5 m 2 x : 2 x 2,25 m Odp. Długość drabiny wynosi 2,25 m.

Slide 20

Bibliografia Matematyka podręcznik dla liceum ogólnokształcącego 1 wyd. Nowa Era W. Babiański, L. Chańko, D. Ponczek Matematyka podręcznik dla liceum ogólnokształcącego 1 wyd. Podkowa A. Cewe, M. Krawczyk, M. Kruk Matematyka podręcznik dla liceum ogólnokształcącego 1 wyd. Nowik S. Zieleń Multimedialna Encyklopedia nauki wyd. AMOS