Twierdzenie Banacha o punkcie stałym

Zobacz slidy

Treść prezentacji

Slide 1

Twierdzenie Banacha o punkcie stałym Piotr Arciszewski

Slide 2

Jedno z twierdzeń Banacha o punkcie stałym dla każdego przekształcenia zwężającego ciąg obrazów punktów (figur) jest zbieżny do punktu stałego. Przekształcenia zwężające, to przekształcenia mające własność powodującą zmniejszanie się odległości punktów po przekształceniu. Przekształcenie takie np. jednokładność w skali 0S1(ma punkt, który przechodzi na siebie samego). Zastosowanie wielokrotne takiej jednokładności przybliża kolejno otrzymywane punkty do środka jednokładności.

Slide 3

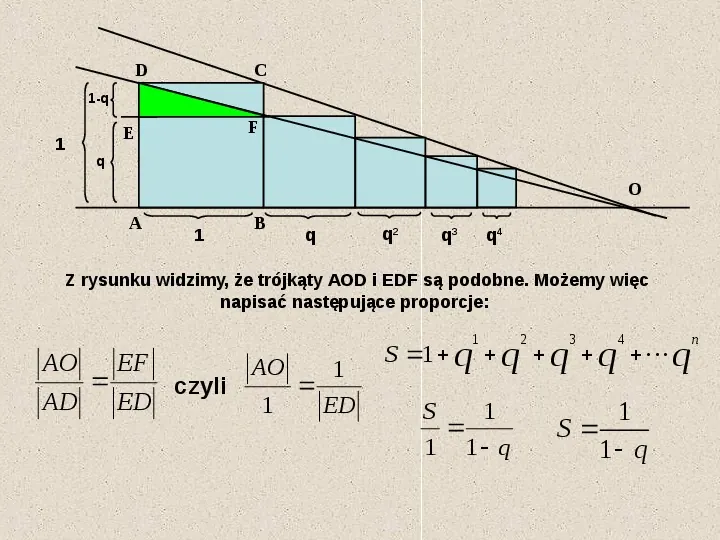
D C 1-q 1 F E q O A 1 B q q2 q3 q4 Z rysunku widzimy, że trójkąty AOD i EDF są podobne. Możemy więc napisać następujące proporcje: 1 AO AD EF ED czyli AO 1 1 ED 2 3 4 S 1 q q q q q S 1 1 1 q 1 S 1 q n

Slide 4

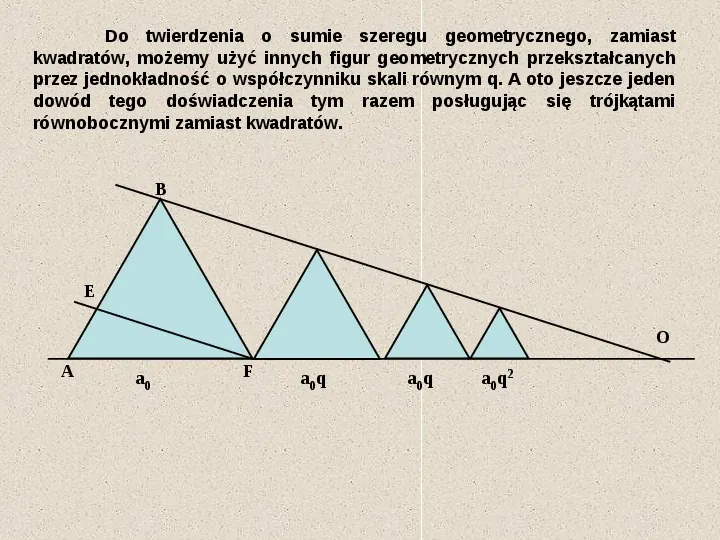
Do twierdzenia o sumie szeregu geometrycznego, zamiast kwadratów, możemy użyć innych figur geometrycznych przekształcanych przez jednokładność o współczynniku skali równym q. A oto jeszcze jeden dowód tego doświadczenia tym razem posługując się trójkątami równobocznymi zamiast kwadratów. B E O A a0 F a0q a0q a0q2

Slide 5

Inne przekształcenie to przekształcenie, które zbliża punkty na osi liczbowej np. 10,5x x Po kolejnym zastosowaniu tego przekształcenia dla dowolnej liczby otrzymujemy wyniki, których kalkulator już nie rozróżnia. O to przykład dla liczby 7. To jest położenie naszej liczby na osi liczbowej. -1 0 1 2 3 4 5 6 7

Slide 6

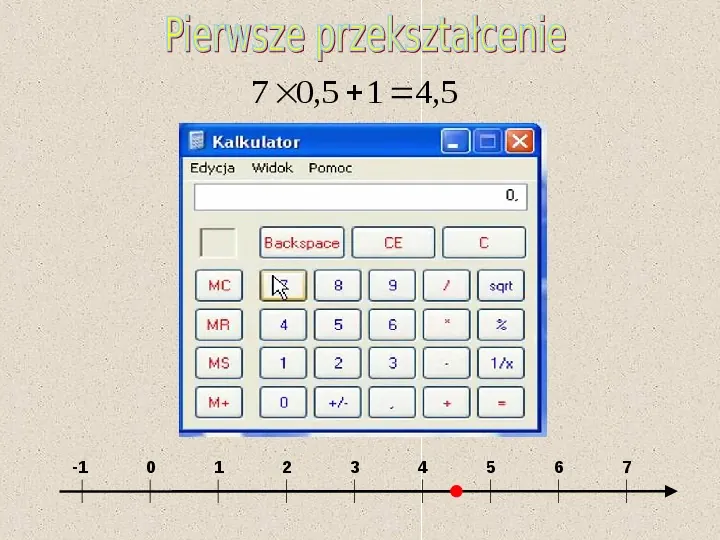
7 0,5 1 4,5 -1 0 1 2 3 4 5 6 7

Slide 7

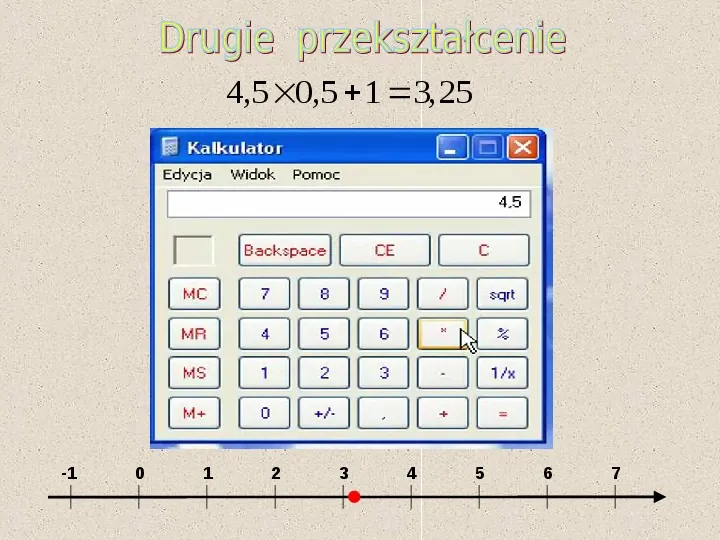
4,5 0,5 1 3,25 -1 0 1 2 3 4 5 6 7

Slide 8

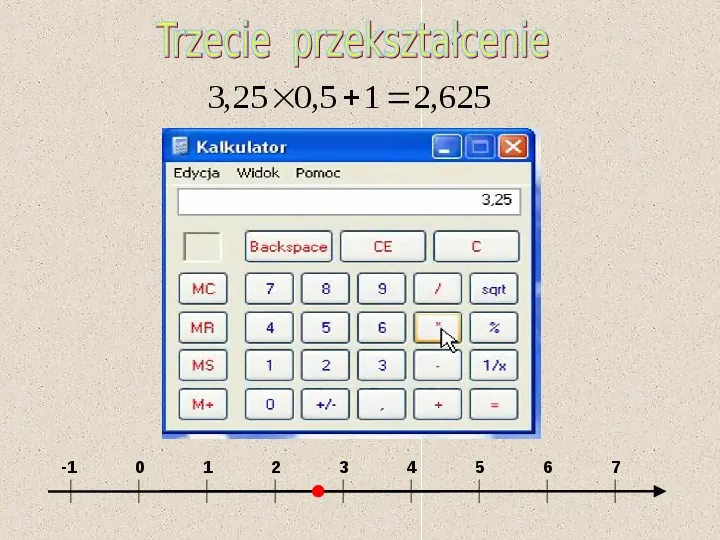
3,25 0,5 1 2,625 -1 0 1 2 3 4 5 6 7

Slide 9

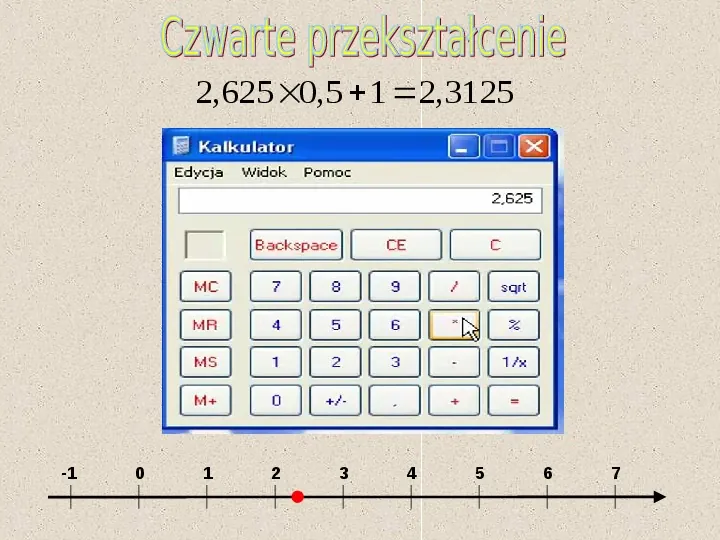
2,625 0,5 1 2,3125 -1 0 1 2 3 4 5 6 7

Slide 10

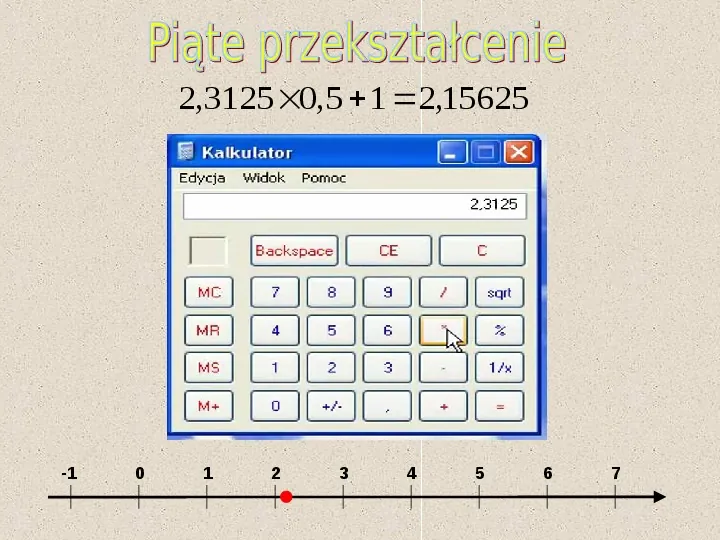
2,3125 0,5 1 2,15625 -1 0 1 2 3 4 5 6 7

Slide 11

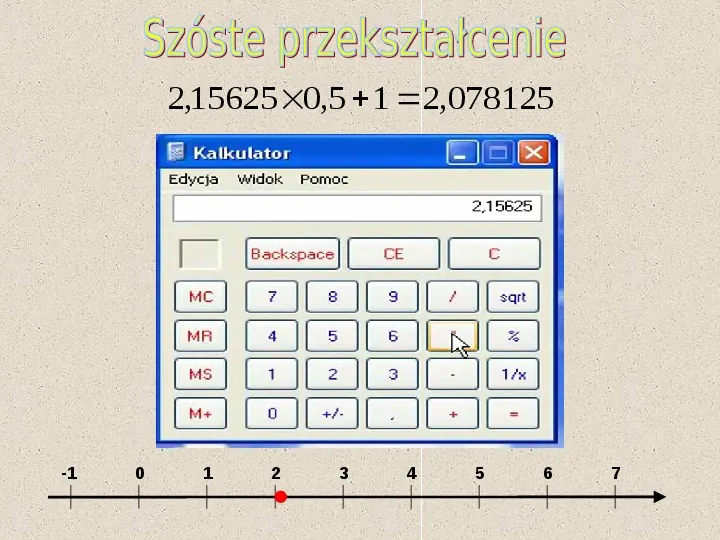
2,15625 0,5 1 2,078125 -1 0 1 2 3 4 5 6 7

Slide 12

To przekształcenie jest rozwiązaniem zadania o cegle: Cegła waży kilo i pół cegły. Ile waży cegła? x 1 0,5x

Slide 13

x 1 0,5x - 0,5x 0,5x 1

Slide 14

x2