Trójkąty

Zobacz slidy

Treść prezentacji

Slide 2

Prezentacja dotyczy następujących tematów: Miara kątów w trójkącie Trójkąty przystające Trójkąty podobne

Slide 3

Podstawowe wiadomości o trójkącie Trójkąt jest obszarem płaszczyzny zawartym między trzema przecinającymi się parami (nie wszystkie w tym samym punkcie) prostymi np. g1, g2 i g3. Mówiąc prościej, trójkąt jest wielokątem z najmniejszą możliwą liczbą wierzchołków trzema. Trójkąt jest prostą figurą, ale jego znaczenie w geometrii jest bardzo duże, m.in. ze względu na to, że wszystkie wielokąty dają się rozłożyć na trójkąty. Ponadto wiele zadań konstrukcyjnych i obliczeniowych można sprowadzić do konstrukcji i obliczeń dotyczących trójkąta

Slide 4

Klasyfikacja trójkątów ze względu na boki

Slide 5

Ogólne twierdzenie dotyczące trójkątów i nie tylko Suma miar kątów wewnętrznych dowolnego trójkąta wynosi zawsze 180 α β γ 180 Znając miary dwóch kątów w trójkącie, automatycznie znamy miarę trzeciego kąta. Każdy trójkąt ma trzy wysokości. Są to odcinki łączące wierzchołki z ich rzutami prostokątnymi na przeciwległe boki lub zawierające je proste. Proste zawierające wysokości trójkąta przecinają się w jednym punkcie zwanym ortocentrum trójkąta.

Slide 6

W trójkącie równobocznym, jak sama nazwa wskazuje, wszystkie boki są tej samej długości. Wynika stąd, że wszystkie kąty w trójkącie równobocznym mają równe miary. Ponieważ suma miar kątów w dowolnym trójkącie wynosi 180, mamy więc: 180 α β γ 3 60 W trójkącie równobocznym odpowiednie środkowe, symetralne boków, dwusieczna kątów i wysokości pokrywają się i długość a 3 ich równa jest 2 , gdzie a jest długością boku trójkąta równobocznego. Wynika z tego też, że środek ciężkości, środek okręgu opisanego, środek okręgu wpisanego i ortocentrum leżą w tym samym punkcie.

Slide 7

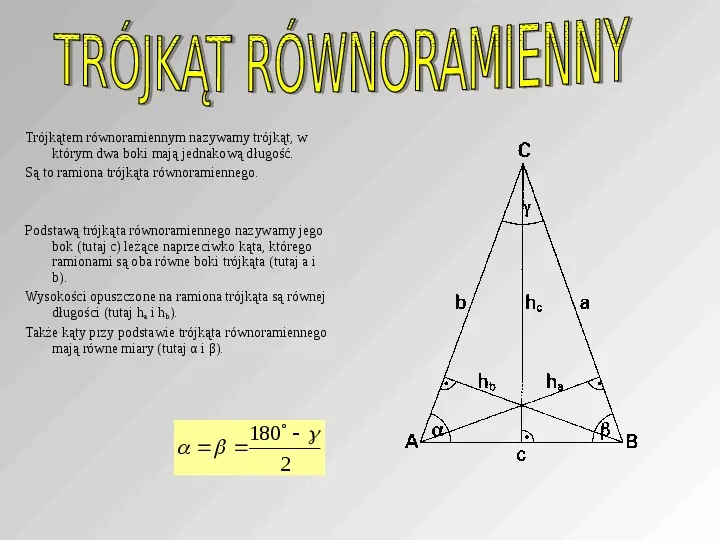
Trójkątem równoramiennym nazywamy trójkąt, w którym dwa boki mają jednakową długość. Są to ramiona trójkąta równoramiennego. Podstawą trójkąta równoramiennego nazywamy jego bok (tutaj c) leżące naprzeciwko kąta, którego ramionami są oba równe boki trójkąta (tutaj a i b). Wysokości opuszczone na ramiona trójkąta są równej długości (tutaj ha i hb). Także kąty przy podstawie trójkąta równoramiennego mają równe miary (tutaj α i β). 180 2

Slide 8

KLASYFIKACJA TRÓJKĄTÓW ZE WZGLĘDU NA KĄTY

Slide 9

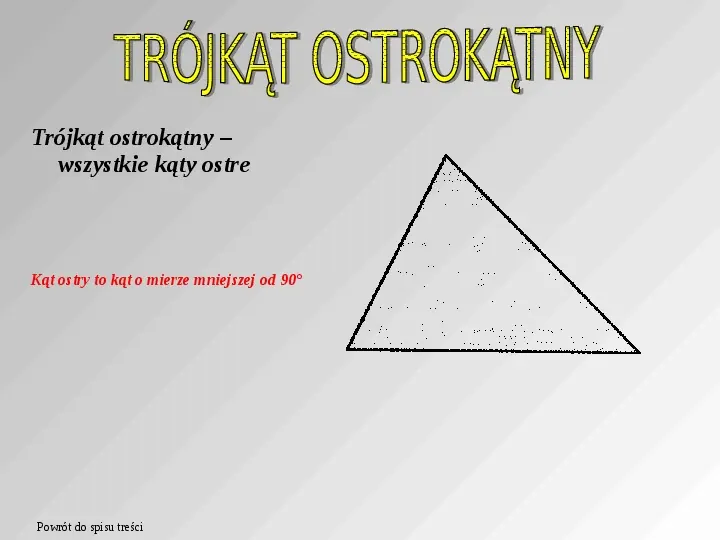
Trójkąt ostrokątny wszystkie kąty ostre Kąt ostry to kąt o mierze mniejszej od 90 Powrót do spisu treści

Slide 10

Trójkąt rozwartokątny jeden kąt rozwarty Kąt rozwarty to kąt o mierze większej od 90 i mniejszej od 180 Powrót do spisu treści

Slide 11

Trójkąt prostokątny jeden kąt prosty Kąt prosty to kąt o mierze równej 90 Najważniejsze i najczęściej używane własności trójkątów prostokątnych są związane z twierdzeniem Pitagoras. a2 b2 c2 Twierdzenie Pitagoras: pole kwadratu zbudowanego na przeciwprostokątnej trójkąta prostokątnego jest równe sumie pól kwadratów zbudowanych na przyprostokątnych tak formułowano twierdzenie Pitagorasa w starożytności. h2 p q Pole kwadratu, którego bok ma długość równą długości wysokości trójkąta opuszczonej z wierzchołka kąta prostego, jest równe polu prostokąta, którego bokami są odcinki,na które ta wysokość dzieli przeciwprostokątną trójkąta.

Slide 13

Do rozstrzygnięcia przystawania dwóch trójkątów bez znaczenia jest ich położenie na płaszczyźnie: czy są względem siebie w odbiciu lustrzanym, obrócone czy przesunięte. Istotne jest, czy ich kąty wewnętrzne mają równe miary, a boki równe długości Trójkąty są przystające , jeśli ich odpowiednie boki i kąty są równe.

Slide 14

CECHA BBB Jeśli trzy boki jednego trójkąta są odpowiednio równe trzem bokom drugiego trójkąta , to są przystające.

Slide 15

CECHA BKB Jeśli dwa boki i kąt zawarty między nimi w jednym trójkącie są odpowiednio równe dwóm bokom i kątowi zawartemu między nim w drugim trójkącie, to te trójkąty są przystające.

Slide 16

CECHA KBK Jeśli bok i dwa kąty leżące przy nim w jednym trójkącie są odpowiednio równe bokowi i dwóm leżącym przy nim kątom w drugim trójkącie, to trójkąty te są przystające.

Slide 18

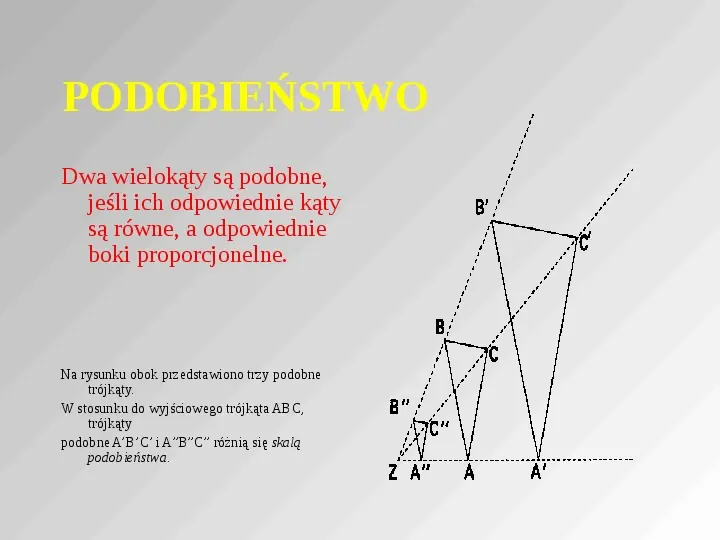
PODOBIEŃSTWO Dwa wielokąty są podobne, jeśli ich odpowiednie kąty są równe, a odpowiednie boki proporcjonelne. Na rysunku obok przedstawiono trzy podobne trójkąty. W stosunku do wyjściowego trójkąta ABC, trójkąty podobne ABC i ABC różnią się skalą podobieństwa.

Slide 19

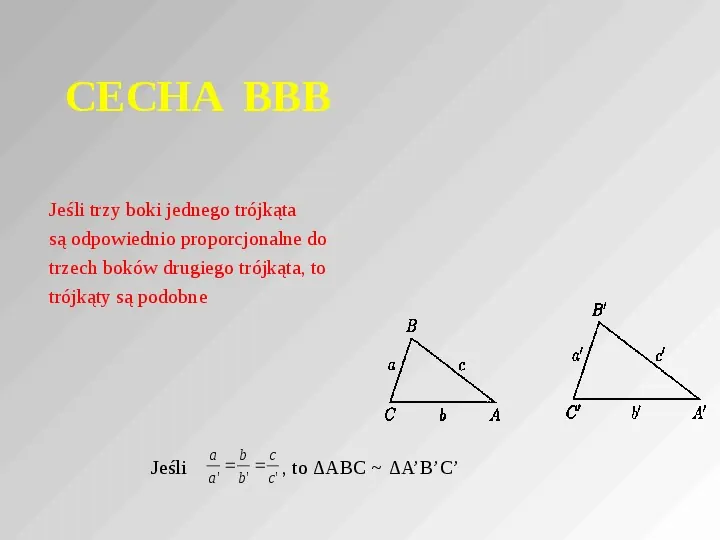
CECHA BBB Jeśli trzy boki jednego trójkąta są odpowiednio proporcjonalne do trzech boków drugiego trójkąta, to trójkąty są podobne Jeśli a b c , a b c to ABC ABC

Slide 20

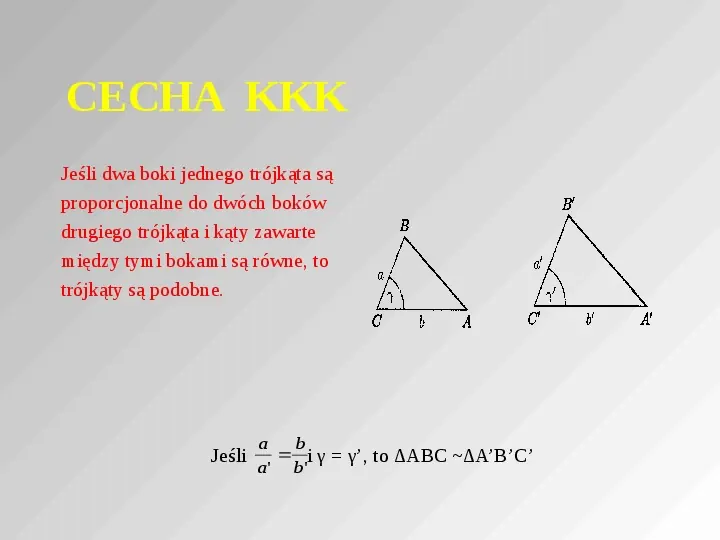
CECHA KKK Jeśli dwa boki jednego trójkąta są proporcjonalne do dwóch boków drugiego trójkąta i kąty zawarte między tymi bokami są równe, to trójkąty są podobne. Jeśli a b i γ γ, to ABC ABC a b

Slide 21

PREZENTACJĘ przygotował: