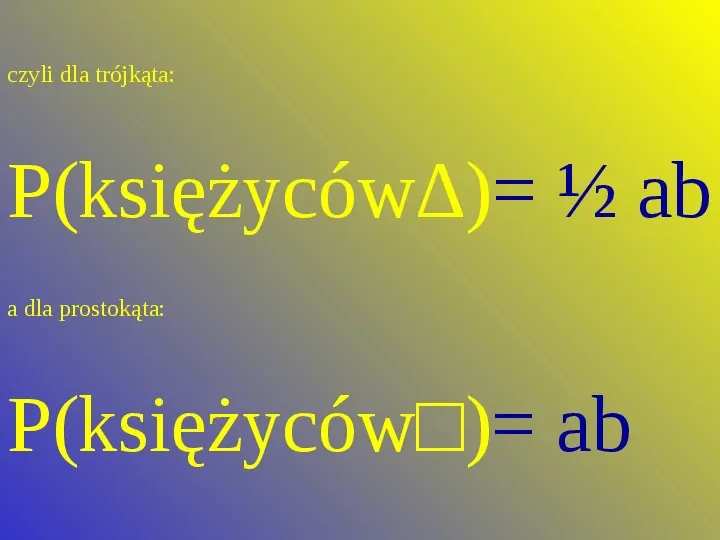Księżyce Hipokratesa

Zobacz slidy

Treść prezentacji

Slide 1

Hipokrates z Chios dowiódł, że suma pól tzw. księżyców Hipokratesa równa się polu powierzchni trójkąta ABC. Jak tego dowiódł?

Slide 2

Czym są księżyce Hipokratesa? Konstrukcja księżyców na trójkącie, prostokącie, trapezie oraz kwadracie. Obliczanie pola powierzchni i obwodów. Co można zauważyć ?

Slide 3

Hipokrates z Chios joński matematyk i sofista. Otworzył szkołę geometrii w Atenach, w latach ok. 450 420 p.n.e. Uczył w tej szkole za opłatą za co usunięto go ze szkoły pitagorejczyków. Prowadząc badania nad kwadraturą koła odkrył księżyce Hipokratesa. gr. Ἱπποκράτης ὁ Χῖος Hippokrates ho Chios,V w. p. n. e

Slide 4

Księżyce Hipokratesa to dwie figury o płaskim kształcie, przypominające sierpy Księżyca, odcięte na płaszczyźnie przez łuki półokręgów, których średnicami są przyprostokątne oraz półokręgu, którego średnicą jest przeciwprostokątna trójkąta prostokątnego. Suma pól księżyców Hipokratesa równa jest polu tego trójkąta. Figury te rozważał Hipokrates z Chios jako konstrukcję pomocniczą w problemie kwadratury koła.

Slide 5

Kwadratura koła to zadanie geometryczne polegające na skonstruowaniu kwadratu o polu równym powierzchni danego koła. Zagadnienie to sformułowano w starożytnej Grecji. Jedną z prób jego rozwiązania były właśnie księżyce Hipokratesa.

Slide 6

Zacznijmy od trójkąta. Należy przygotować odpowiednie przybory do zadań konstrukcyjnych, a następnie:

Slide 7

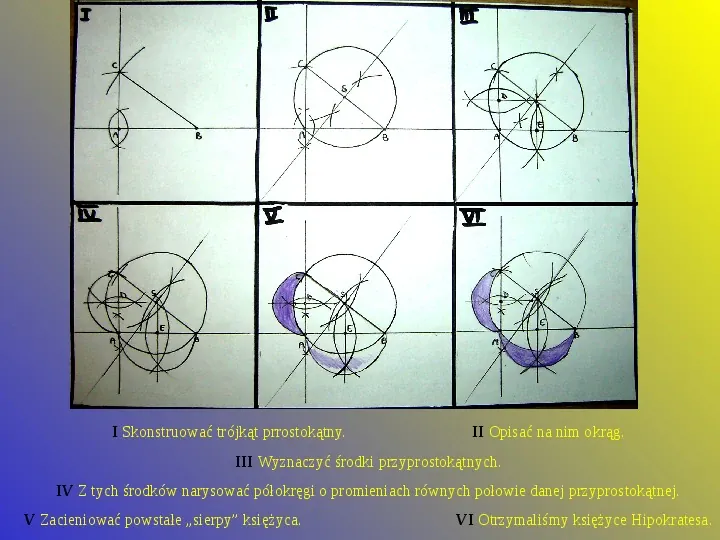
I Skonstruować trójkąt prrostokątny. II Opisać na nim okrąg. III Wyznaczyć środki przyprostokątnych. IV Z tych środków narysować półokręgi o promieniach równych połowie danej przyprostokątnej. V Zacieniować powstałe sierpy księżyca. VI Otrzymaliśmy księżyce Hipokratesa.

Slide 8

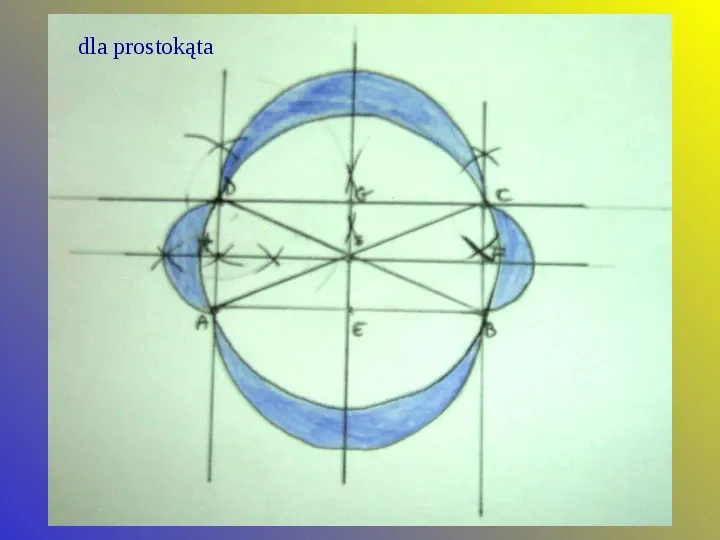
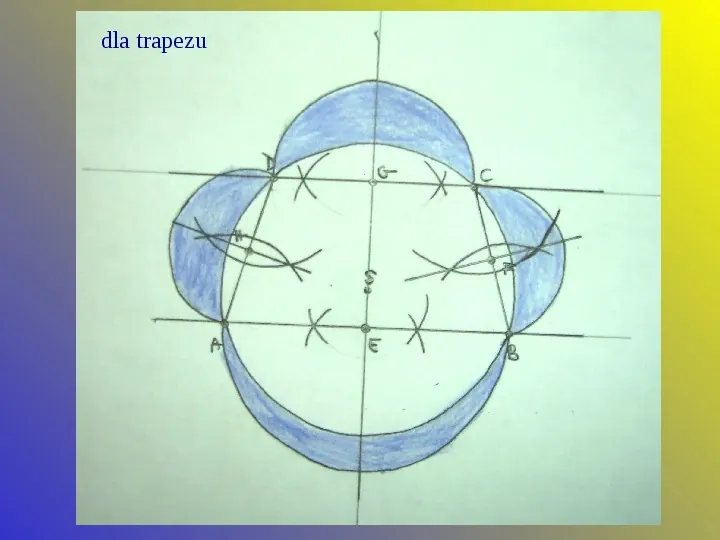
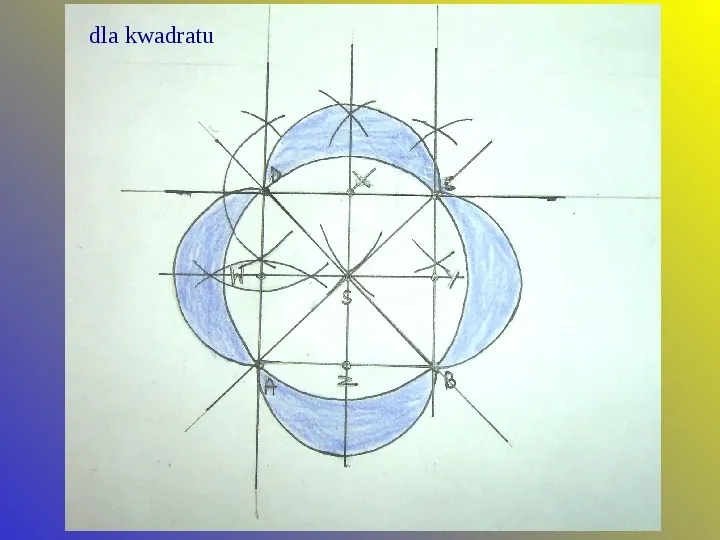
Kolejne konstrukcje księżyców wykonuje się w sposób analogiczny. Najpierw konstruując daną figurę, a następnie opisując na niej okręgi i wyznaczając środki wszystkich boków. Ostatnią czynnością jest narysowanie półokręgów ze wszystkich środków o promieniu równym boku.

Slide 9

dla prostokąta

Slide 10

dla trapezu

Slide 11

dla kwadratu

Slide 12

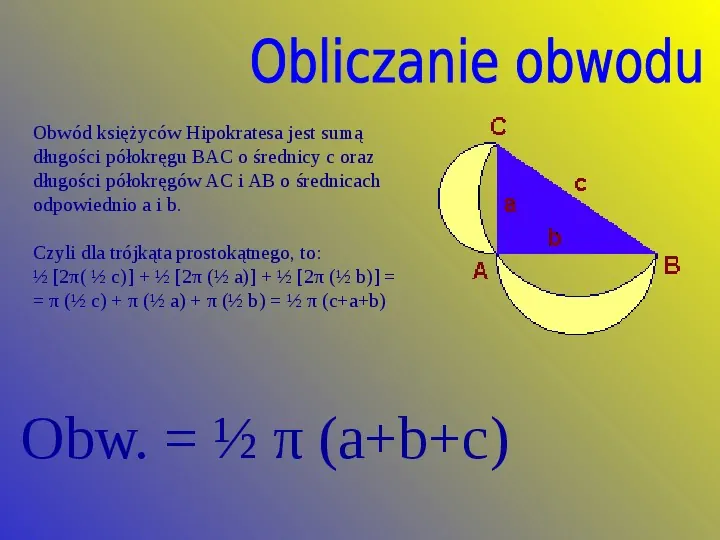
Obwód księżyców Hipokratesa jest sumą długości półokręgu BAC o średnicy c oraz długości półokręgów AC i AB o średnicach odpowiednio a i b. Czyli dla trójkąta prostokątnego, to: [2π( c)] [2π ( a)] [2π ( b)] π ( c) π ( a) π ( b) π (cab) Obw. π (abc)

Slide 13

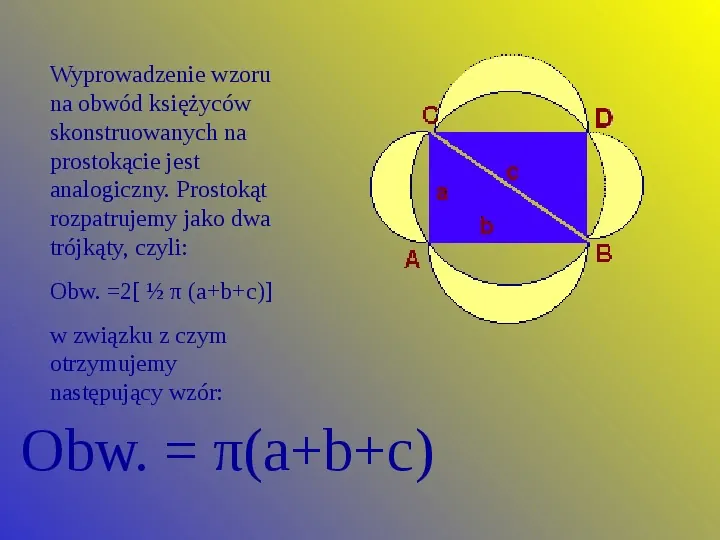
Wyprowadzenie wzoru na obwód księżyców skonstruowanych na prostokącie jest analogiczny. Prostokąt rozpatrujemy jako dwa trójkąty, czyli: Obw. 2[ π (abc)] w związku z czym otrzymujemy następujący wzór: Obw. π(abc)

Slide 14

W przypadku gdy wielokąt jest prostokątem lub trójkątem prostokątnym suma pól księżyców Hipokratesa jest równa polu tego prostokąta lub trójkąta prostokątnego (odpowiednio).

Slide 15

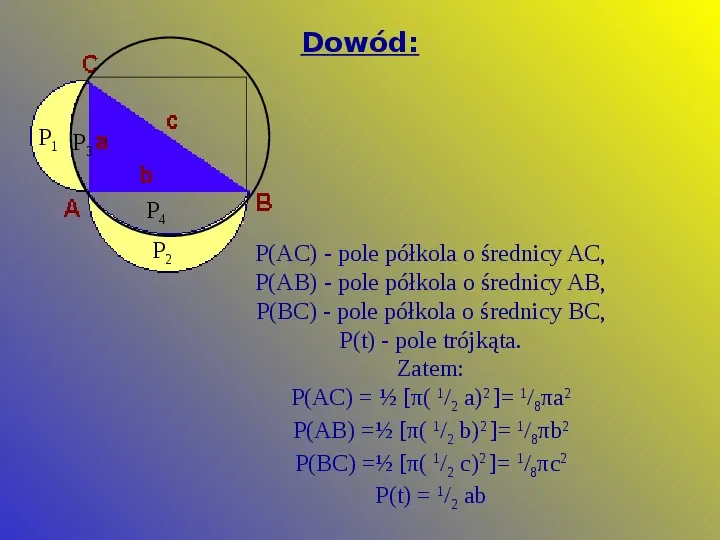
Dowód: P1 P3 P4 P2 P(AC) - pole półkola o średnicy AC, P(AB) - pole półkola o średnicy AB, P(BC) - pole półkola o średnicy BC, P(t) - pole trójkąta. Zatem: P(AC) [π( 12 a)2 ] 18πa2 P(AB) [π( 12 b)2 ] 18πb2 P(BC) [π( 12 c)2 ] 18πc2 P(t) 12 ab

Slide 16

P1P2 pole księżyców P1P2 [P(AC) P(AB)] - (P3 P4 ) P3P4 P(BC) - P(t) P1P2 (18πa2 18π b2) - [18π c2 - P(t)] P1P2 (18π a2 18π b2) - 18π c2 P(t) Z Twierdzenia Pitagorasa: 1 8π a2 18π b2 18π c2 P1 P3 Po podstawieniu: P4 P1P2 18π c2 - 18π c2 P(t) P2 P1P2 P(t)12 ab Suma pól żółtych księżyców jest równa polu trójkąta prostokątnego.

Slide 17

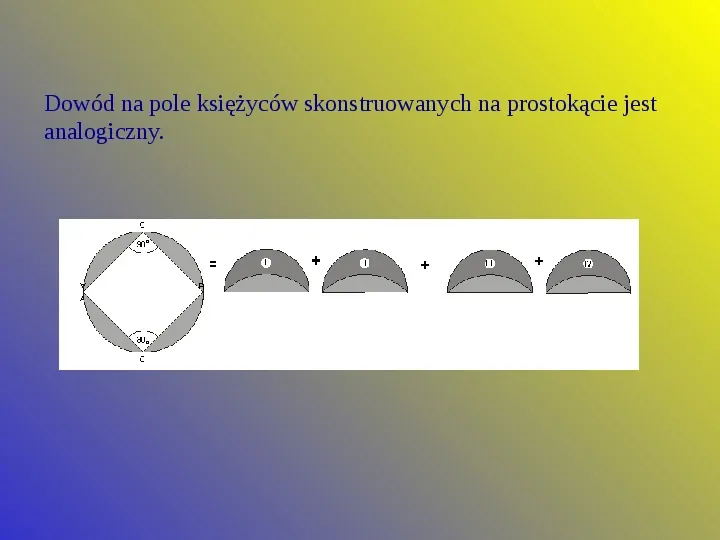
Dowód na pole księżyców skonstruowanych na prostokącie jest analogiczny.

Slide 18

czyli dla trójkąta: P(księżyców) ab a dla prostokąta: P(księżyców) ab

Slide 20

Zagadnienie kwadratury koła sprowadza się do konstrukcji za pomocą linijki i cyrkla takiego kwadratu, którego pole równałoby się polu danego koła. Podane przez Hipokratesa wyjątkowo proste rozwiązanie kwadratury jego księżyców zachęcało wielkie umysły matematyczne do szukania rozwiązania kwadratury koła, figury stanowczo prostszej pod względem kształtu geometrycznego.

Slide 21

Przez przeszło 2000 lat najpotężniejsze umysły matematyczne trudzą się nad rozwiązaniem tego zagadnienia. Niezliczone próby przedstawienia takiej konstrukcji bez wyjątku kończyły się fiaskiem. Przez tysiące lat matematycy zajmowali się tym zagadnieniem, nie mogąc problemu rozwiązać, ani też nie mogąc dowieść, że jest to niewykonalne. Zainteresowanie tym problemem zaćmiewa nawet do pewnego stopnia pozostałe dwa klasyczne problemy matematyczne starożytności - problem trysekcji kąta i podwojenia kostki.

Slide 22

W 1883 niemiecki matematyk F. Lindemann udowodnił (poprzez udowodnienie przestępności liczby π tzn. posiadania nieskończonej liczby cyfr rozwinięcia dziesiętnego ) niemożność dokonania tego za pomocą cyrkla i linijki. W ten sposób udowodniono, że jeden z najstarszych problemów matematycznych kwadratura koła jest niemożliwa.

Slide 23

Kwadratura koła stała się synonimem nierozwiązywalnego zadania. Wyrażenie to weszło do języka potocznego dla określenia skazanych na niepowodzenie prób podejmowanych przez kogoś, kto upiera się, by zrealizować coś niemożliwego.

Slide 24

Można zauważyć, że księżyce Hipokratesa można skonstruować na każdym wielokącie, na którym można opisać okrąg (tzn. gdy wszystkie jego wierzchołki leżą na tym okręgu), czyli: wtedy i tylko wtedy, gdy symetralne wszystkich jego boków przecinają się w jednym punkcie.

Slide 25

Można również zauważyć, że księżyce Hipokratesa skonstruowane na trójkącie prostokątnym równoramiennym mają jednakowe pola, co wykorzystuje się przy rozwiązywaniu zagadnienia kwadratury księżyców Hipokratesa.

Slide 26

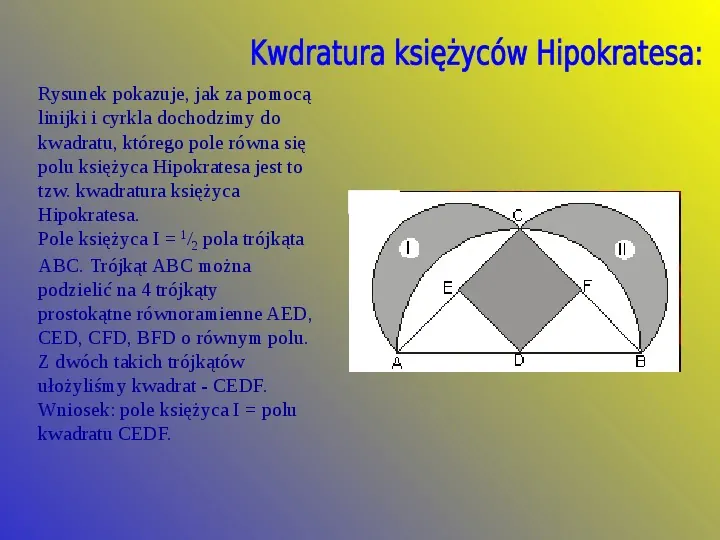
Rysunek pokazuje, jak za pomocą linijki i cyrkla dochodzimy do kwadratu, którego pole równa się polu księżyca Hipokratesa jest to tzw. kwadratura księżyca Hipokratesa. Pole księżyca I 12 pola trójkąta ABC. Trójkąt ABC można podzielić na 4 trójkąty prostokątne równoramienne AED, CED, CFD, BFD o równym polu. Z dwóch takich trójkątów ułożyliśmy kwadrat - CEDF. Wniosek: pole księżyca I polu kwadratu CEDF.

Slide 27

1. Encyklopedia powrzechna PWN, Warszawa 1984, wydanie trzecie. 2. Słownik encyklopedyczny MATEMATYKA, wyd. Europa, Wrocław 1998. 3. Tablice matematyczne, wyd. Podkowa, Gdańsk 2003. 4. 500 zagadek matematyczny (wydanie czwarte), Wiedza Powrzechna, Warszawa 1974. 5. http:pl.wikipedia.orgwikiHipokrateszChios 6. http:www.spmargonin.republika.plabacusksiezyce.html 7. http:portalwiedzy.onet.pl50855,,,,ksiezycehipokratesa,haslo.html 8. http:kkk2002ar.w.interia.plkshipo.html 9. http:www.zsee.bytom.pliwonastronastronkapliki444.html

Slide 28

Dziękuję za uwagę