Historia matematyki

Zobacz slidy

Treść prezentacji

Slide 1

Historia matematyki. Matematyka jest alfabetem, przy pomocy którego  Bóg opisał wszechświat. (Galileusz)

Slide 2

Spis treści Prehistoria Starożytny Wschód Chiny Mezopotamia Egipt Grecja Suwak logarytmiczny Mnożenie Dzielenie Dokładność Wielcy matematycy Bibliografia Autorzy

Slide 3

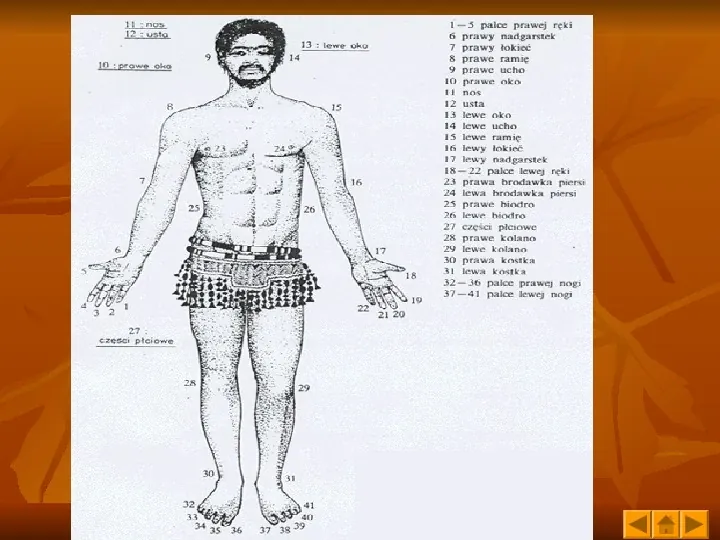
Prehistoria Liczby raz i dwa są na pewno pierwotnymi pojęciami liczebników w historii ludzkiej. Te pierwotne rozróżnienia są doskonale widoczne w starożytnych językach i pismach. Zaczęło się od rozróżniania gramatycznego pomiędzy liczbami pojedynczą, podwójną oraz mnogą, występującego u wielu różnych ludów. Przykładowo u starożytnych greków ho lykos znaczyło wilk, natomiast to lykos to były dwa wilki, a hoj lykos oznaczało wilki. W starodawnym chińskim znaczenie lasu było wyrażone przez powtarzający trzykrotnie piktogram drzewo, natomiast pojęcie tłumu oznaczał obrazek człowieka trzykrotnie narysowany. Prosty stąd wniosek, że starożytni nie używali liczby trzy chcąc jedynie przedstawić trzy elementy, lecz także w odniesieniu do ogólnej mnogości. Tak więc pierwotnie człowiek nie potrafił operować wielkimi liczbami, wystarczały mu liczebniki jeden i dwa, a wszystkie większe określał jako dużo. W dalszym toku ewolucji człowieka począł on wykonywać pierwszych, jeszcze bardzo prymitywnych rachunków. Zaczynało się od różnego rodzaju nacięć (najczęściej były one na kości). Przykładowo prehistoryczny pasterz musiał policzyć 88 owiec, siadał niedaleko jaskini mając kawałek kości i krzemień. Każde przejście pojedynczej owcy powodowało, że robił nacięcie więcej. Sprawdzając nacięcia łatwo mógł zobaczyć czy całe stado powróciło do domu, czy jakaś owca mu się nie zgubiła. Inny prymitywny sposób liczenia polegał na posługiwaniu się częściami ciała. Jednakże ten sposób był dobry jedynie przy niewielkich ilościach przedmiotów do policzenia. Polegał on na dotykaniu się w odpowiednie części ciała w określonej kolejności. Poniższy rysunek przedstawia jedną z opcji jaką posługiwali się prehistoryczni:

Slide 5

Kość z Ishango, znaleziona w źródłach Nilu (północno-wschodnie Kongo) pochodzi sprzed 20 tysięcy lat (górny paleolit). Jedna z typowych interpretacji głosi, że jest to najwcześniejsza znana demonstracja liczb pierwszych. Przeddynastyczni Egipcjanie z 5 tysiąclecia p.n.e. graficznie przedstawiali geometryczne konstrukcje przestrzenne. Geometryczne przedstawienia okręgu, elipsy, trójek pitagorejskich można odnaleźć na monumentach w Anglii i Szkocji z 3 millenium p.n.e.

Slide 6

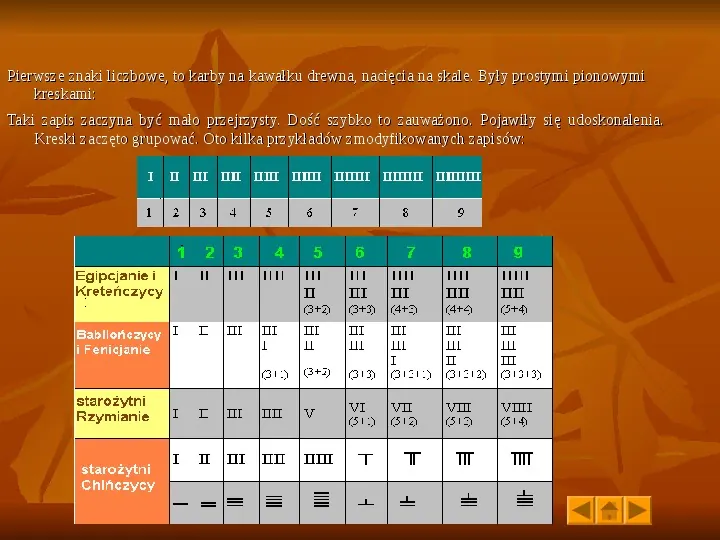
Pierwsze znaki liczbowe, to karby na kawałku drewna, nacięcia na skale. Były prostymi pionowymi kreskami: Taki zapis zaczyna być mało przejrzysty. Dość szybko to zauważono. Pojawiły się udoskonalenia. Kreski zaczęto grupować. Oto kilka przykładów zmodyfikowanych zapisów:

Slide 7

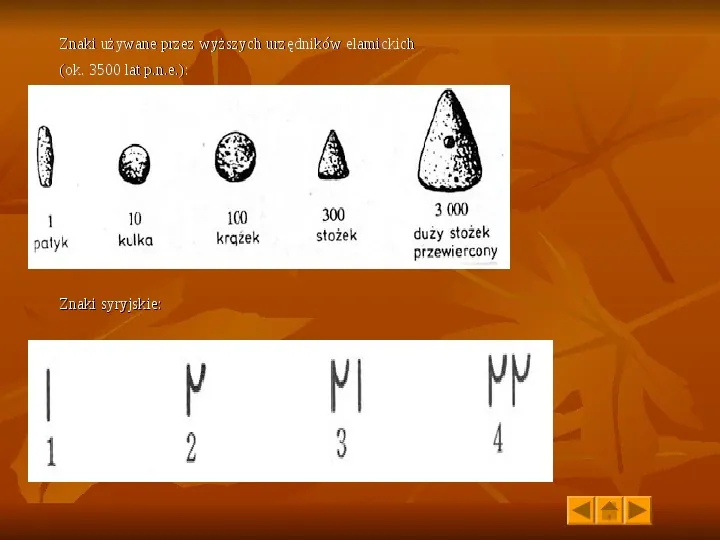
Znaki używane przez wyższych urzędników elamickich (ok. 3500 lat p.n.e.): Znaki syryjskie:

Slide 8

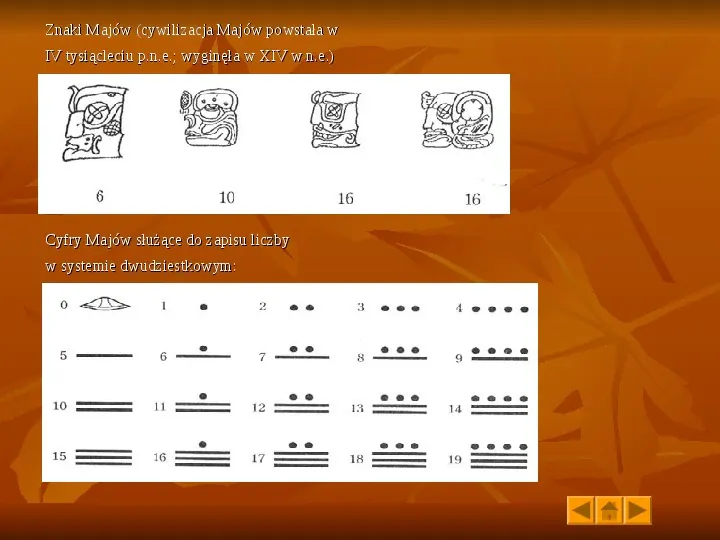
Znaki Majów (cywilizacja Majów powstała w IV tysiącleciu p.n.e.; wyginęła w XIV w n.e.) Cyfry Majów służące do zapisu liczby w systemie dwudziestkowym:

Slide 9

Starożytny Wschód Chiny W 212 p.n.e. chiński cesarz Qin Shi Huang (Shi Huang-ti) rozkazał spalić wszystkie książki spoza państwa Qin. Rozkaz ten nie wszędzie został wykonany, jednak w konsekwencji niewiele dziś wiadomo o starożytnej matematyce chińskiej. Najwcześniejszy istniejący do dziś matematyczny artefakt z Chin to pochodząca z epoki Shang (1600 p.n.e.1046 p.n.e.) skorupa żółwia z zapisaną liczbą 123. Użyty jest system dziesiętny, od góry do dołu wydrapane zostały: cyfra 1, symbol setki, cyfra 2, symbol dziesiątki, cyfra 3. Podówczas był to najbardziej zaawansowany system liczbowy na świeci. Późniejsi Chińczycy liczyli na przyrządach takich jak suanpan i chiński abakus. Nie wiadomo dokładnie, kiedy suan pan został wynaleziony, najwcześniejsza wzmianka znajduje się w Dodatku do sztuki figur Xu Yue z roku 190 n.e.. Najstarsza chińska praca z odniesieniami do geometrii, która przetrwała palenie ksiąg, Mo Jing, pochodzi z filozoficznego kanonu motizmu napisana ok. 330 p.n.e.. Skompilowana została przez zwolenników Mocjusza (470390 p.n.e.). Opisywała rozmaite aspekty fizyki, przy okazji omawiając też stosowane metody matematyczne.

Slide 10

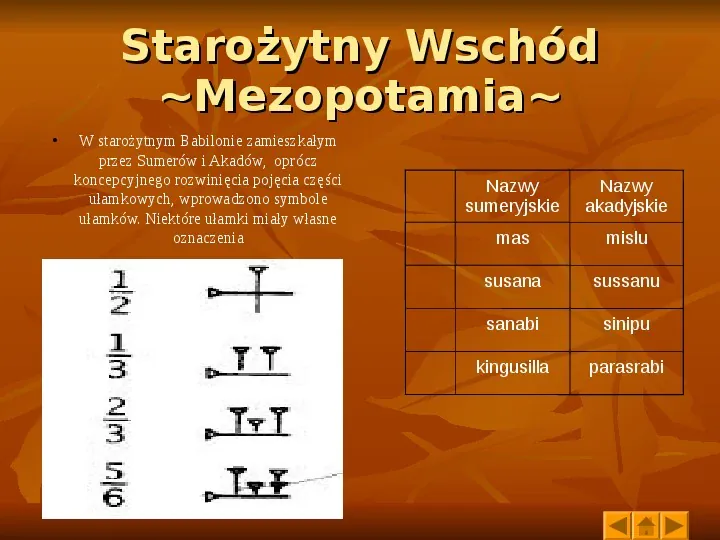
Starożytny Wschód Mezopotamia W starożytnym Babilonie zamieszkałym przez Sumerów i Akadów, oprócz koncepcyjnego rozwinięcia pojęcia części ułamkowych, wprowadzono symbole ułamków. Niektóre ułamki miały własne oznaczenia Nazwy sumeryjskie Nazwy akadyjskie mas mislu susana sussanu sanabi sinipu kingusilla parasrabi

Slide 11

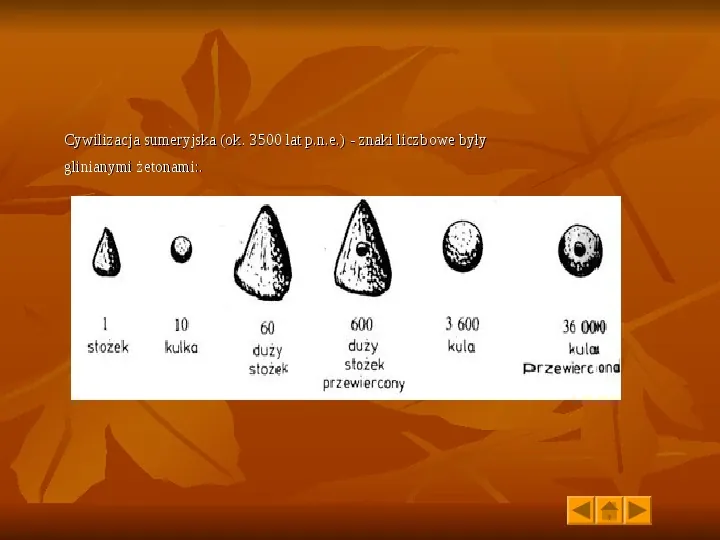
Cywilizacja sumeryjska (ok. 3500 lat p.n.e.) - znaki liczbowe były glinianymi żetonami:.

Slide 12

Starożytny Wschód Egipt Dodawanie czyli pogrupuj i przegrupuj Zwróćmy najpierw uwagę, jak współcześnie dodajemy do siebie dwie liczby. 689 234 923 Zaczynamy od jednostek: 9 plus 4 równa się 13, trzynaście jednostek. Zapisujemy 3 jednostki, a pozostałe 10 jednostek dodamy do następnej dodawanej grupy, dziesiątek. Następnie dodajemy dziesiątki: 8 plus 3 plus jedna dziesiątka, która uzbierała się nam z dodawania jednostek, równa się 12 dziesiątek. Zapisujemy 2 dziesiątki, a pozostałe dziesięć dziesiątek, czyli jedną setkę, dodamy podczas sumowania następnej grupy, setek. Na koniec dodajemy setki: 6 plus 2 plus jedna setka, która uzbierała się z dodawania dziesiątek, równa się 9 setek. Zapisujemy 9 setek.

Slide 13

A jak dodawali Egipcjanie? W gruncie rzeczy tak samo, tylko, nie mając cyfr, grupowali symbole: równa się dodać 234 689 równa się równa się 923

Slide 14

Jak zapisać liczenie czyli zbyt wiele kresek... Starożytni Egipcjanie, podobnie jak wiele innych ludów, zapisywanie liczb zaczęli od bardzo prostej metody. Jedna pionowa kreska oznaczała, że policzono jeden przedmiot, dwie kreski dwa przedmioty, trzy kreski trzy, cztery kreski cztery. Im większą liczbę trzeba zanotować, tym bardziej uciążliwy staje się ten sposób. Wyobraźmy sobie, że chcemy zapisać liczbę 82: Mnóstwo kresek wymaga sporo pracy przy pisaniu. A przy odczytywaniu? Sprawdź, czy powyżej rzeczywiście zapisano liczbę 82.

Slide 15

Kiedy Egipcjanie rozwinęli swoje pismo, hieroglify, dla większych liczb wymyślili specjalne symbole. Liczby od 1 do 9 nadal zapisywano odpowiednią ilością pionowych kresek. Ale już 10 zapisywano specjalnym, pojedynczym znakiem rysunkiem pięty. 1 2 3 4 5 6 7 8 9

Slide 16

A następne liczby? Polskie jede-na-ście oznacza jeden-na-dziesięcie, czyli 101, dwanaście to 102, trzynaście to 103. W podobny sposób spojrzeli na to Egipcjanie. Liczby następujące po 10 zapisywali rysując znak dziesiątki oraz odpowiednią liczbę znaków jednostek. Podobnie dwa-dzieścia to dwie dziesiątki, dwadzieścia jeden to dwie dziesiątki i jeden, dwadzieścia dwa to dwie dziesiątki i dwa. Trzy-dzieści to trzy dziesiątki... i tak dalej aż do dziewięć-dziesiąt dziewięć. 10 11 12 13 19 20 21 22 23 29 90 91 92 93 99

Slide 17

Do zapisania liczby 100 trzeba by już było użyć dziesięciu symboli dziesiątki. Poradzono sobie z tym wprowadzając kolejny symbol, wyobrażający zwinięty sznur mierniczy. Podobnie jak w przypadku liczb od 11 do 99, liczby od 101 do 999 zapisywano używając odpowiedniej liczby znaków dla setek, dziesiątek i jedności. Jak łatwo się domyślić, dla tysiąca wymyślono kolejny znak, przedstawiający kwiat lotosu. Z kolei dziesięć tysięcy symbolizował wizerunek palca wskazującego, sto tysięcy rysunek kijanki czy też ryby, zaś milion wyobrażała sylwetka klęczącego człowieka wznoszącego ręce w górę w geście zdumienia. 100 1000 10.000 100.000 1.000.000

Slide 18

Jak widać, do zapisania liczby 348 trzeba było użyć 15 symboli: 3 symboli setki, 4 symbole dziesiątki i 8 symboli jednostki. W przeciwieństwie do naszego współczesnego, dziesiętnego pozycyjnego sposobu zapisu, w którym 348 oznacza inną liczbę niż 843, w systemie stosowanym przez Egipcjan pojedynczy znak oznacza faktycznie liczbę, a nie cyfrę, więc zmiana kolejności ani wymieszanie symboli nie zmieniało wartości zanotowanej liczby. Egipcjanie pisali zazwyczaj od prawej do lewej, odwrotnie niż my, ale często także od góry na dół, albo od lewej do prawej.Stosowane jako znaki hieroglificzne sylwetki ludzi lub zwierząt skierowane były w jedną lub drugą stronę, odczytywać je należało wychodząc im naprzeciw, tak żeby napotykać ich wzrok. Ponieważ ważną rolę odgrywały względy estestyczne, często napisom umieszczanym po dwu stronach jakiegoś malowidła nadawano symetryczny kierunek. Pełne barw hieroglify biegły po jednej stronie z lewa na prawo, po drugiej odwrotnie, po obu stronach rzędy napisów kierowały się ku centrum sceny. Przy poziomym piśmie małe lub poziome znaki umieszczano jeden nad drugim, zamiast stawiać je w rzędzie; przy pionowym zapisie wysmukłe znaki stawiano jeden przy drugim, zamiast jeden nad drugim. Całość miała wyglądać ładnie. 348 4622

Slide 19

Mnożenie czyli sprytne dodawanie Znowu mnóstwo kresek Jak widać, dodawanie w systemie zapisu używanym w starożytnym Egipcie było równie proste jak obecnie, tylko że z braku cyfr często trzeba było rysować wiele jednakowych znaków. Zupełnie inaczej wygląda sprawa z mnożeniem. Przemnożenie np. liczby 37 przez 2 to to samo, co dodanie do siebie 3737, więc mnożenie przez dwa było równie łatwe, co dodawanie. Jak jednak poradzić sobie z mnożeniem, kiedy obie liczby są całkiem spore? Ile jest ryb w 16 koszach, jeśli każdy kosz mieści 27 ryb, teoretycznie można by było obliczać rysując siedemnaście razy symbole składające się na liczbę 27, a następnie grupując to wszystko... Niezbyt zachęcające! Zaraz, zaraz, czy powiedzieliśmy, że mnożenie przez dwa jest łatwe? Egipcjanie skorzystali właśnie z tego faktu. Zauważmy, że do policzenia, ile jest 1627, nie potrzeba powtarzać 16 razy rysunku liczby 27. Wystarczy zauważyć, że 16 82 (42)2 ((22)2)2. Zamiast sumować elementy z szesnastu rysunków liczby 27 można równie dobrze wykonać cztery podwojenia. Podwojenia czyli zwykłe dodawania:

Slide 20

27 27 54 ( 27 2) dwa kosze ryb 54 54 108 ( 27 4) cztery kosze ryb 108 108 216 ( 27 8) osiem koszy ryb 216 216 432 ( 2716) szesnaście koszy ryb Metodą podwajania, czyli dodawania takich samych liczb, uzyskaliśmy wynik mnożenia. Dobrze się złożyło, że mieliśmy przemnożyć przez 16, liczbę, która powstaje przez same podwojenia. A co zrobić w przypadku mnożenia przez inną liczbę?

Slide 21

Nieco trudniejsze mnożenie Każdy z robotników powinien dostać miar zboża. Ilu miar zboża potrzebuje dla swoich pracowników nadzorca grupy robotników? W pierwszym rzędzie tabeli widzimy, że dla 1 robotnika potrzeba 13 miar zboża. Drugi rząd powstał przez podwojenie obu liczb z pierwszego rzędu. Wynika z niego, że dla 2 robotników potrzeba 26 miar zboża. W trzecim rzędzie mamy kolejne podwojenie dla 4 robotników potrzeba 52 miary zboża. Czwarty rząd nie zawiera liczby robotników, bo służy tylko uporządkowaniu zapisu liczby 52 uzyskanej z prostego podwojenia symboli składajacych się na liczbę 26. W pierwszym rzędzie tabeli widzimy, że dla 1 robotnika potrzeba 13 miar zboża. Drugi rząd powstał przez podwojenie obu liczb z pierwszego rzędu. Wynika z niego, że dla 2 robotników potrzeba 26 miar zboża. W trzecim rzędzie mamy kolejne podwojenie dla 4 robotników potrzeba 52 miary zboża. Czwarty rząd nie zawiera liczby robotników, bo służy tylko uporządkowaniu zapisu liczby 52 uzyskanej z prostego podwojenia symboli składajacych się na liczbę 26. Ale przecież 4 robotników i 2 robotników i jeszcze 1 robotnik to razem 7 robotników, czyli tylu, dla ilu mamy zapewnić żywność! Skoro łączna liczba robotników jest taka, o jaką nam chodzi, to również łączna liczba miar zboża dla nich. W kolejnym wierszu zapisu przepisujemy po prostu wszystkie symbole miar zboża dla 1, 2 i 4 robotników. Na koniec w uzyskanej sumie zamieniamy dziesięć symboli jednostek na symbol dziesiątki. Otrzymany wynik brzmi: 9 dziesiątek oraz 1 jednostka, czyli 91. Jeśli każdy robotnik dostaje po 13 miar zboża, to dla 7 robotników potrzeba 91 miar zboża.

Slide 22

Najstarszymi zachowanymi dokumentami matematycznymi w Egiptu są papirusy Rhinda (od nazwiska nabywcy), napisany przez Ahmesa oraz papirus moskiewski, nabyty przez W.S. Golenieszewa. Oba pochodzą z mniej więcej tego samego okresu, ale są kopiami tekstów z około 1900 roku p.n.e. Papirus Rhinda zaczyna się od słów: Przepis do osiągnięcia poznania wszelkich rzeczy ciemnych... wszelkich tajemnic, które są zawarte w przedmiotach. Ułożona była ta księga w roku 33, Mesori dnia... za króla Górnego i Dolnego Egiptu RA-A-US życie dającego według wzoru starych pism, które wygotowane były za czasów króla (RAEN-M-AT). Oto pisarz Ahmes pisał kopię tę (zob. Krysicki i Mikosz. 2000). Niektórzy autorzy nazywają papirus Rhinda podręcznikiem Ahmesa do matematyki, ze względu na podane w nim liczne zadania, których treść przekraczała ówczesne potrzeby praktyczne. Oto przykłady kilku zadań, pochodzących z tego papirusu: znajdź liczbę, jeśli wiadomo, że po dodaniu do niej tej liczby i po odjęciu od otrzymanej sumy tejże sumy otrzymuje się w wyniku liczbę 10, ktoś wyjął ze skarbca zawartości. Z tego, co pozostało, podjęto i wówczas w skarbcu pozostało 150. Ile była na początku w skarbcu? każda z siedmiu osób ma po siedem kotów. Każdy kot zjadł siedem myszy, każda mysz zjadła po siedem kłosów, a z każdego kłosa może wyrosnąć siedem miar zboża. Ile tu było osób, kotów, kłosów i miar zboża? A ile tych wszystkich rzeczy razem?

Slide 23

Starożytny Wschód Grecja Podobnie jak w Egipcie, w Grecji w najstarszym okresie używano ułamków o liczniku 1. Oznaczano je pomijając licznik, za pomocą liter alfabetu o numerze odpowiadającym danej liczbie naturalnej, przy czym u góry z prawej strony litery dopisywano u góry dwie kreseczki, np: b, g, d, e, z, x, h, t. Ułamki o liczniku różnym od jedności zapisywano w sposób następujący: najpierw licznik, następnie kreseczka u góry oddzielająca licznik od mianownika i na koniec mianownik z dwoma kreseczkami zapisany dwukrotnie, np.: ka kg kg, lb me me. Arabowie przejmując zdobycze matematyki, rozprzestrzenili je po całej Azji Mniejszej. Używał ich Alchwarizmi urodzony około roku 800 w Chiwie, w dzisiejszym Uzbekistanie. To od zniekształcenia jego nazwiska powstał termin algorytm, a od tytułu jego traktatu o równaniach Hisab al.-djabr wal mukabala ( O odtwarzaniu i przeciwstawianiu) pochodzi wyraz algebra. Dopiero w początkach XII wieku trafiły do średniowiecznej Europy. Wtedy to została wydana książka pt. Liber abaci, czyli Księga abaku (abak prototyp używanego do niedawna suwaka, rzymskiego przyrządu do liczenia). Napisał ją włoski kupiec z Pizzy o imieniu Leonardo znany jako Fibonacci, po odbyciu licznych podróży do Bizancjum, Syrii i Egiptu, w czasie których poznał osiągnięcia matematyków tych krajów. Treścią Liber abaci były najważniejsze zagadnienia ówczesnej matematyki, usystematyzowane przez autora wiadomości zaczerpnięte z prac arabskich oraz własne przemyślenia, zadania i metody.

Slide 24

SYSTEM LICZBOWY STAROŻYTNYCH GREKÓW Podczas pierwszego millenium przed narodzeniem Chrystusa w Grecji nie istniały obowiązujące normy państwowe, gdyż poszczególne wyspy greckie tworzyły oddzielne państwa. Oznacza to, że każde z nich miało swoją własną walutę, system wag i miar, a system liczbowy nieznacznie różnił się. W owych czasach liczby wykorzystywano głównie w transakcjach handlowych. Istniały również inne systemy liczbowe zaproponowane przez różnych greckich matematyków, ale nie weszły one do powszechnego zastosowania. Pierwszym greckim systemem liczbowym, któremu się przyjrzymy jest system akrofoniczny, który stosowany był w pierwszym milenium przed naszą erą. Akrofoniczny oznacza, iż symbole liczb pochodzą od pierwszej litery nazwy liczby, tak więc symbol pochodzi od skrótu nazwy liczby. Oto symbole dla liczb 5, 10, 100, 1000, 10000. Akrofoniczne  5,  10, 100, 1000,  10000.

Slide 25

Opuściliśmy symbol dla jedności, czyli I, która jest naturalną prostą notacją nie pochodzącą z żadnej pierwszej litery cyfry. Dla cyfry 5 symbolem powinien być P, jeżeli nazwa brzmi Pente; jednak później nastąpiły zmiany w greckim alfabecie, a nazwa liczby pozostała bez zmian. Pierwotnie Pente brzmiało Gente. System liczbowy był oparty o zasadę addytywności, podobnie jak liczby rzymskie. Oznacza to, że 8 jest po prostu VIII, czyli symbol 5 razem z dodanymi trzema symbolami jedności. Oto 1 10 w greckim systemie akrofonicznym.

Slide 26

5678 drachm było zapisywane w ten sposób: 3807 talentów byłoby zapisane w sposób następujący: 3807 drachm i 3 obole:

Slide 27

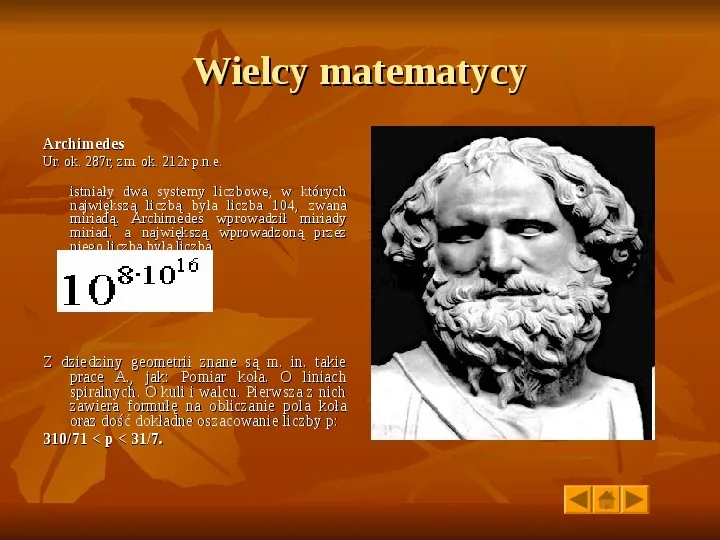
Wielcy matematycy Archimedes Ur. ok. 287r, zm. ok. 212r p.n.e. istniały dwa systemy liczbowe, w których największą liczbą była liczba 104, zwana miriadą. Archimedes wprowadził miriady miriad. a największą wprowadzoną przez niego liczbą była liczba Z dziedziny geometrii znane są m. in. takie prace A., jak: Pomiar koła. O liniach spiralnych. O kuli i walcu. Pierwsza z nich zawiera formułę na obliczanie pola koła oraz dość dokładne oszacowanie liczby p: 31071 p 317.

Slide 28

Pitagoras (ok. 572-497 p.n.e), filozof grecki. Pochodził z wyspy Samos, czyli wschodniej kolonii jońskiej. Mając lat 40 opuścił Jonię, która walczyła z Persami, i odbył liczne podróże, również do Indii, gdzie zetknął się z tamtejszymi systemami filozoficzno-religijnymi.Przebywał w Tracji, ostatecznie osiadł jednak w Wielkiej Grecji, gdzie w Krotonie założył szkołę filozoficzno-religijną i związek pitagorejski. Nie pozostawił po sobie żadnych dzieł, a te, które później rozpowszechniano w Grecji, były, jak podają historycy filozofii, apokryfami. Przeprowadził dowód twierdzenia nazwanego twierdzeniem Pitagorasa (znanego wcześniej jako reguła bez dowodu), odkrył niewspółmierność boku i przekątnej kwadratu, przypisywał magiczne własności liczbom, wierzył w harmonię w kosmosie.

Slide 29

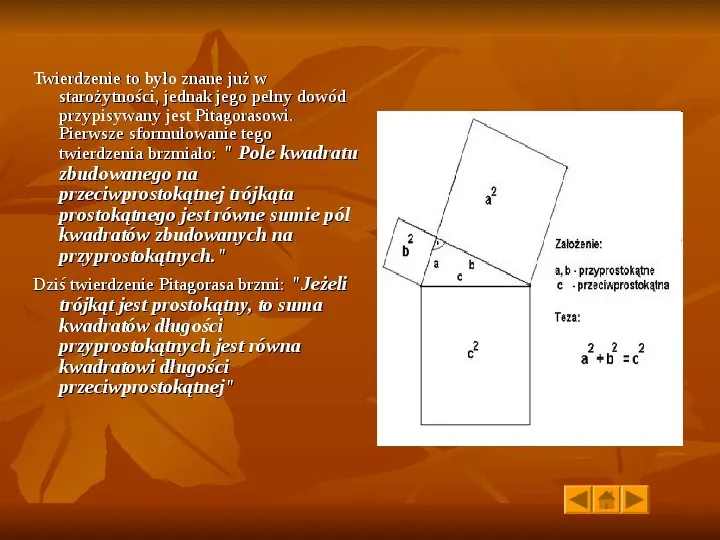
Twierdzenie to było znane już w starożytności, jednak jego pełny dowód przypisywany jest Pitagorasowi. Pierwsze sformułowanie tego twierdzenia brzmiało: Pole kwadratu zbudowanego na przeciwprostokątnej trójkąta prostokątnego jest równe sumie pól kwadratów zbudowanych na przyprostokątnych. Dziś twierdzenie Pitagorasa brzmi: Jeżeli trójkąt jest prostokątny, to suma kwadratów długości przyprostokątnych jest równa kwadratowi długości przeciwprostokątnej

Slide 30

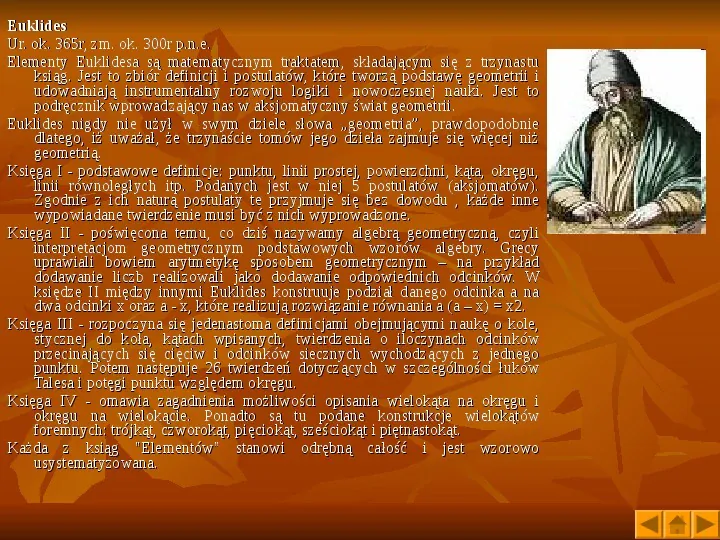
Euklides Ur. ok. 365r, zm. ok. 300r p.n.e. Elementy Euklidesa są matematycznym traktatem, składającym się z trzynastu ksiąg. Jest to zbiór definicji i postulatów, które tworzą podstawę geometrii i udowadniają instrumentalny rozwoju logiki i nowoczesnej nauki. Jest to podręcznik wprowadzający nas w aksjomatyczny świat geometrii. Euklides nigdy nie użył w swym dziele słowa geometria, prawdopodobnie dlatego, iż uważał, że trzynaście tomów jego dzieła zajmuje się więcej niż geometrią. Księga I - podstawowe definicje: punktu, linii prostej, powierzchni, kąta, okręgu, linii równoległych itp. Podanych jest w niej 5 postulatów (aksjomatów). Zgodnie z ich naturą postulaty te przyjmuje się bez dowodu , każde inne wypowiadane twierdzenie musi być z nich wyprowadzone. Księga II - poświęcona temu, co dziś nazywamy algebrą geometryczną, czyli interpretacjom geometrycznym podstawowych wzorów algebry. Grecy uprawiali bowiem arytmetykę sposobem geometrycznym na przykład dodawanie liczb realizowali jako dodawanie odpowiednich odcinków. W księdze II między innymi Euklides konstruuje podział danego odcinka a na dwa odcinki x oraz a - x, które realizują rozwiązanie równania a (a x) x2. Księga III - rozpoczyna się jedenastoma definicjami obejmującymi naukę o kole, stycznej do koła, kątach wpisanych, twierdzenia o iloczynach odcinków przecinających się cięciw i odcinków siecznych wychodzących z jednego punktu. Potem następuje 26 twierdzeń dotyczących w szczególności łuków Talesa i potęgi punktu względem okręgu. Księga IV - omawia zagadnienia możliwości opisania wielokąta na okręgu i okręgu na wielokącie. Ponadto są tu podane konstrukcje wielokątów foremnych: trójkąt, czworokąt, pięciokąt, sześciokąt i piętnastokąt. Każda z ksiąg Elementów stanowi odrębną całość i jest wzorowo usystematyzowana.

Slide 31

TALES z MILETU (640-546 p.n.e.) jest pierwszym znanym z nazwiska greckim mędrcem. O jego życiu wiemy niewiele. Starożytni pisarze nazwali go pierwszym filozofem, fizykiem, matematykiem, astronomem. Wyrósł w bujnej atmosferze życia małoazjatyckich kolonii, w których element grecki odgrywał rolę pośrednika w handlu między Wschodem a Grecją właściwą, następnie zaś między Wschodem a Zachodem. Z kontaktów handlowych wywodzi się zapewne i oddziaływanie kultury babilońskiej i egipskiej na małoazjatyckich Greków. Platon wspomina, że gdy Tales obserwował gwiazdy, wpadł do studni i piękna niewolnica miała się wyrazić żartem, iż chciał zobaczyć, co się dzieje na niebie, a nie dostrzegł, co znajduje się pod jego nogami. Anegdota ta jednak nie charakteryzuje postawy Talesa. Nie był on oderwanym od życia myślicielem, lecz człowiekiem nad wyraz praktycznym, który umiał wykorzystać posiadaną wiedzę w swoich transakcjach handlowych. Proklos, komentator pierwszej księgi Elementów Euklidesa w oparciu o zaginioną Historię geometrii Euklidesa, przypisuje Talesowi autorstwo następujących twierdzeń geometrycznych: 1. Dowód, że średnica dzieli koło na połowy. 2. Odkrycie, obok szeregu innych twierdzeń, że kąty przypodstawne w trójkącie równoramiennym są równe. 3. Twierdzenie o równości kątów wierzchołkowych i o przystawaniu trójkątów o równym boku i przyległych dwu kątach.

Slide 32

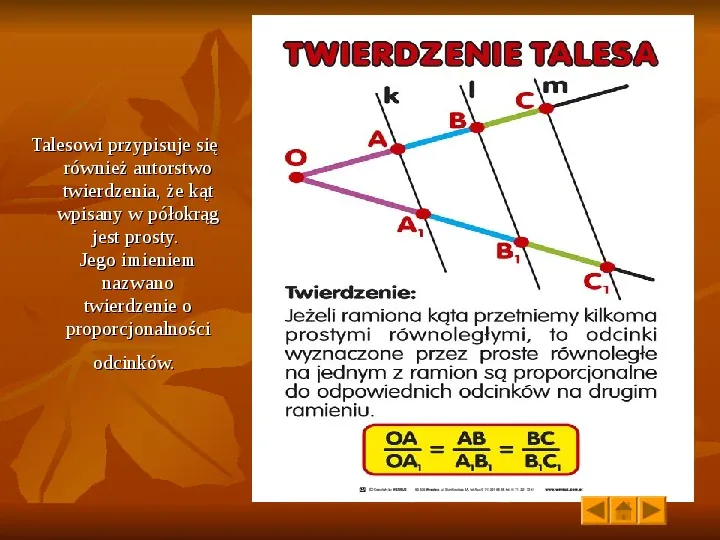
Talesowi przypisuje się również autorstwo twierdzenia, że kąt wpisany w półokrąg jest prosty. Jego imieniem nazwano twierdzenie o proporcjonalności odcinków.

Slide 33

Suwak logarytmiczny Suwak logarytmiczny (suwak rachunkowy) prosty przyrząd ułatwiający obliczenia, powszechnie używany przez inżynierów do końca lat 80. XX wieku. Wynaleziony w 1632 roku przez Williama Oughtreda, zainspirowany linijką logarytmiczną Edmunda Guntera. Suwak logarytmiczny działa na zasadzie dodawania logarytmów poprzez dodawanie różnej długości odcinków zaznaczonych na skali. Jest to praktyczne wykorzystanie równości: Tym samym mnożenie sprowadza się do dodawania (w przypadku suwaka dodawania odcinków na skalach). Suwak logarytmiczny umożliwia mnożenie, dzielenie i wiele innych działań np. logarytmowanie, potęgowanie, pierwiastkowanie. Spełnia rolę tablic trygonometrycznych. Niekiedy posiada dodatkowe znaczniki lub skale pozwalające szybko obliczać powierzchnię koła, ciężar i wytrzymałość prętów itp. Suwak logarytmiczny z sumatorem (addatorem) do dodawania i odejmowania liczb 6-cyfrowych. Najczęściej wykonany jest w postaci linijki o długości skali 25 lub 12,5 cm z przesuwką i okienkiem, ale bywają także suwaki okrągłe. Wykonywane są także suwaki do specjalnych zadań np. na tej zasadzie działa tabela naświetlań w fotografii czy komputer samochodowy z lat 60. Do wad należy brak możliwości dodawania i odejmowania w większości modeli (niektóre suwaki mają wbudowany sumator do dodawania i odejmowania jak np. suwaki przedsiębiorstwa Castell), oraz ograniczona dokładność (23 cyfry znaczące dla typowego suwaka). Wiele wzorów wymagających dodawania lub odejmowania można przekształcić do postaci zawierającej tylko zwiększenie albo zmniejszenie zawartości o jeden. Dodanie 1 jest łatwe w pamięci. Zegarek naręczny z obrotowym suwakiem logarytmicznym. Na zdjęciu pokazano przykład przeliczenia mil morskich (znacznik NAUT) na kilometry (znacznik KM) - 10 mil morskich to ok. 18,5 km. W Polsce suwaki produkowane były seryjnie przez przedsiębiorstwo Skala ze skalą o długości 25 i 12,5 cm.

Slide 34

Dokładność Dokładność obliczeń wykonywanych przy pomocy suwaka jest zależna od precyzji wykonania suwaka i umiejętności operatora. Zakładając poprawne wykonanie suwaka, oraz że operator potrafi odróżnić na podziałce odległość 0,25mm, wówczas dokładność odczytu można wyliczyć ze wzoru: gdzie l jest długością skali suwaka podaną w milimetrach. Stąd wniosek, że im dłuższa skala, tym większa dokładność odczytu. Dla standardowego suwaka o długości 250mm, błąd wynosi 0,1 odczytywanej liczby. Suwaki precyzyjne Istnieją także suwaki precyzyjne, gdzie podziałkę liczb naturalnych podzielono na dwie części. Pierwszą, zawierającą liczby od 1 do sqrt 10 umieszczono w miejscu podziałek (C) i (D) Drugą, zawierającą liczby od sqrt 10 do 10 umieszczono w miejscu podziałek (A) i (B) Pozwala to uzyskać dokładność, jak na zwykłym suwaku, o dwukrotnie dłuższej skali.

Slide 35

Mnożenie Na podziałce (A) znaleźć pierwszy czynnik iloczynu i ustawić nad nim 1 lub 10 podziałki (B). Na podziałce (B) odnaleźć drugi czynnik i ustawić na nim kresę okienka. Kresa wskazuje na podziałce (A) wynik mnożenia (pamiętać o ustaleniu ilości miejsc dziesiętnych). Przykład: Mnożenie 2x3. Jedynka przesuwki ustawiona nad pierwszym czynnikiem . Wynik odczytujemy pod drugim czynnikiem . Zauważmy, że w takim ustawieniu możemy odczytać wszystkie inne mnożenia przez 2.

Slide 36

Dzielenie Na podziałce (A) ustawić kresę okienka na dzielnej. Podziałkę (B) ustawić tak, aby dzielnik znalazł się pod kresą okienka. Wynik ilorazu znajduje się pod 1 lub pod 10 przesuwki. Przykład: Dzielenie 12. Dzielna na przesuwce ustawiona nad dzielnikiem. Wynik odczytujemy nad jedynką dolnej skali. Przesuwka została przesunięta w lewo, więc wynik należy podzielić przez 10 co daje 0,5. Zauważmy, że równie dobrze mogłoby to być dzielenie 102.

Slide 37

Bibliografia Internet: www.wikipedia.pl, http:hjkgfg.fm.interia.plhistoria.htm Anna Osipowicz, Lingua latina lingua nostra, Warszawa: wydawnictwo MAG. Marek Kordos, Wykłady z historii matematyki, wydawnictwo SCRIPT.

Slide 38

Wykonały: Marlena Stalica Magdalena Łudzik, kl. 2 a