Ułamki zwykłe

Zobacz slidy

Treść prezentacji

Slide 1

UŁAMKI ZWYKŁE powtórzenie (WŁASNOŚCI UŁAMKÓW ZWYKŁYCH DZIAŁANIA WYKONYWANE NA UŁAMKACH ZWYKŁYCH)

Slide 2

POKAZ ZAWIERA INFORMACJE MIĘDZY INNYMI O : UŁAMKACH WŁAŚCIWYCH DODAWANIU UŁAMKÓW UŁAMKACH NIEWŁAŚCIWYCH ODEJMOWANIU UŁAMKÓW SKRACANIU I ROZSZERZANIU UŁAMKÓW MNOŻENIU UŁAMKÓW PORÓWNYWANIU UŁAMKÓW DZIELENIU UŁAMKÓW

Slide 3

Ułamek składa się z trzech elementów: Licznika Kreski ułamkowej Mianownika LICZNIK 32 KRESKA UŁAMKOWA MIANOWNIK 57

Slide 4

UŁAMEK JAKO WYNIK Z DZIELENIA TO WYNIK Z DZIELENIA : DZIELNA JEST LICZNIKIEM , DZIELNIK MIANOWNIKIEM , A KRESKA UŁAMKOWA ZASTĘPUJE ZNAK DZIELENIA Np. DZIELNA 3 3:4 4 DZIELNIK ILORAZ

Slide 5

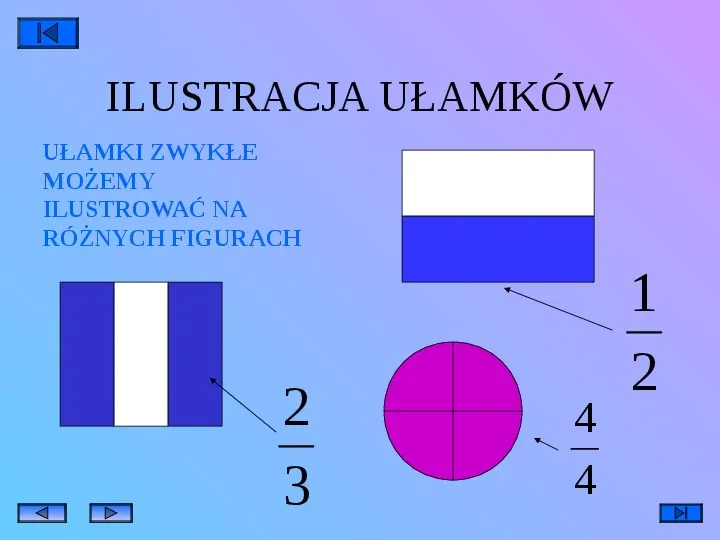
ILUSTRACJA UŁAMKÓW UŁAMKI ZWYKŁE MOŻEMY ILUSTROWAĆ NA RÓŻNYCH FIGURACH 2 3 4 4 1 2

Slide 6

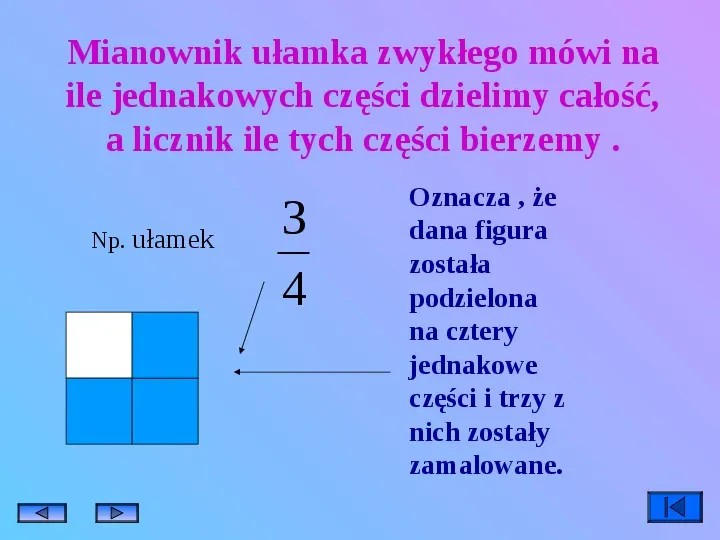
Mianownik ułamka zwykłego mówi na ile jednakowych części dzielimy całość, a licznik ile tych części bierzemy . Np. ułamek 3 4 Oznacza , że dana figura została podzielona na cztery jednakowe części i trzy z nich zostały zamalowane.

Slide 7

Ułamki właściwe Ułamki właściwe to takie , w których licznik jest zawsze mniejszy od mianownika . np. 1 3 7 8 1 , , , , 2 58 19 229 1000 Ułamki właściwe są mniejsze od jednej całości . Ułamki właściwe 0 1

Slide 8

Ułamki niewłaściwe Ułamki niewłaściwe to takie , w których licznik jest zawsze większy od mianownika lub równy mianownikowi. Ułamki niewłaściwe 0 1 2 np. 12 263 37 298 1000 , , , , 2 48 19 229 1000 Ułamki właściwe są większe lub równe jednej całości .

Slide 9

LICZBY MIESZANE Z UŁAMKÓW NIEWŁAŚCIWYCH MOŻEMY WYŁĄCZYĆ CAŁOŚĆ . W TYM CELU DZIELIMY LICZNIK UŁAMKA PRZEZ JEGO MIANOWNIK : Przykłady liczb mieszanych : RESZTA Z DZIELENIA 17 2 17 : 5 3 5 5 PO WYŁĄCZENIU CAŁOŚCI OTRZYMUJEMY LICZBY MIESZANE 2 4 9 1 8 ,98 ,550 ,3 7 19 45 8

Slide 10

ZAMIANA LICZB MIESZANYCH NA UŁAMKI NIEWŁAŚCIWE Liczby mieszane można zamienić z powrotem na ułamki niewłaściwe : np. Dodajemy licznik 2 30 4 7 7 Mnożymy mianownik przez całość Mianownik przepisujemy bez zmian

Slide 11

SKRACANIE UŁAMKÓW ZWYKŁYCH Ułamki zwykłe możemy skracać dzieląc licznik i mianownik ułamka przez tą samą liczbę różną od 0 i 1. :5 15 3 25 5 :5 Ułamki zwykłe skracamy do momentu uzyskania ułamków nieskracalnych

Slide 12

UŁAMKI NIESKRACALNE Ułamki zwykłe skracamy aż do momentu , kiedy otrzymamy ułamki nieskracalne . Ułamki nieskracalne to takie , których nie da się już więcej skrócić . Licznik i mianownik ułamka nieskracalnego są liczbami względnie pierwszymi . Wartość ułamka przed i po skróceniu jest taka sama np. 2 1 4 2

Slide 13

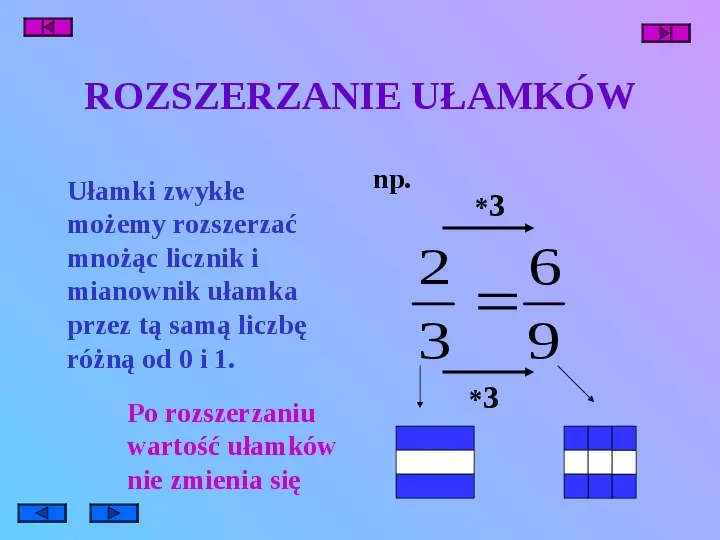
ROZSZERZANIE UŁAMKÓW Ułamki zwykłe możemy rozszerzać mnożąc licznik i mianownik ułamka przez tą samą liczbę różną od 0 i 1. Po rozszerzaniu wartość ułamków nie zmienia się np. 3 2 6 3 9 3

Slide 14

Porównywanie ułamków zwykłych Z dwóch ułamków o jednakowych mianownikach większy jest ten , który ma większy licznik. Np. 3 5 8 8 Z dwóch ułamków o jednakowych licznikach większy jest ten , który ma mniejszy mianownik. Np. Ułamki właściwe są zawsze mniejsze od ułamków niewłaściwych ! 5 5 11 8

Slide 15

Porównywanie różnych ułamków ABY PORÓWNAĆ UŁAMKI ZWYKŁE O RÓŻNYCH LICZNIKACH I MIANOWNIKACH , NALEŻY SPROWADZIĆ UŁAMKI DO TEGO SAMEGO MIANOWNIKA LUB LICZNIKA .(Można to zrobić poprzez rozszerzanie lub skracanie ułamków). Np. 4 3 ... 7 5 Wstawiamy znak mniejszości Porównujemy rozszerzając 20 21 12 12 lub 35 35 21 20

Slide 16

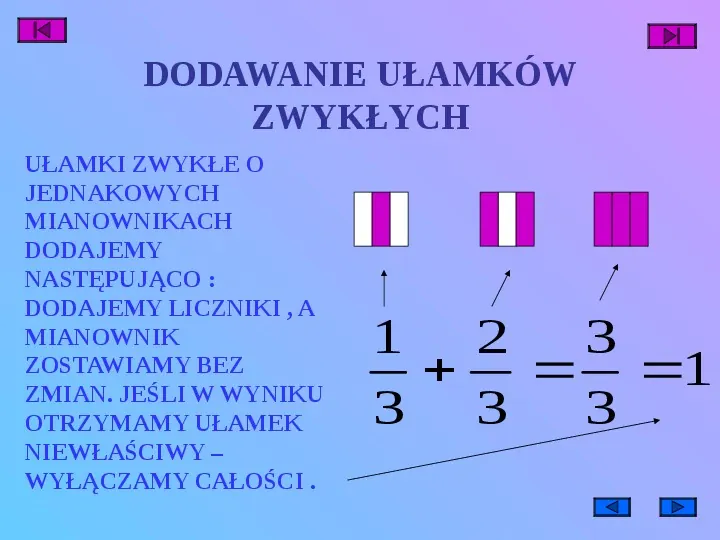
DODAWANIE UŁAMKÓW ZWYKŁYCH UŁAMKI ZWYKŁE O JEDNAKOWYCH MIANOWNIKACH DODAJEMY NASTĘPUJĄCO : DODAJEMY LICZNIKI , A MIANOWNIK ZOSTAWIAMY BEZ ZMIAN. JEŚLI W WYNIKU OTRZYMAMY UŁAMEK NIEWŁAŚCIWY WYŁĄCZAMY CAŁOŚCI . 1 2 3 1 3 3 3

Slide 17

ODEJMOWANIE UŁAMKÓW ZWYKŁYCH UŁAMKI ZWYKŁE O NP. JEDNAKOWYCH MIANOWNIKACH 2 5 9 5 2 ODEJMUJEMY a)1 NASTĘPUJĄCO : 7 7 7 7 7 ODEJMUJEMY LICZNIKI , 2 7 13 7 6 A MIANOWNIK b)3 2 2 11 11 11 11 11 ZOSTAWIAMY BEZ ZMIAN. JEŚLI NIE DA SIĘ 3 7 19 7 12 ODJĄĆ LICZNIKÓW ZAMIENIAMY CAŁOŚCI ABY OTRZYMAĆ UŁAMEK NIEWŁAŚCIWY. 3 c)3 2 2 2 16 16 16 16 16 4

Slide 18

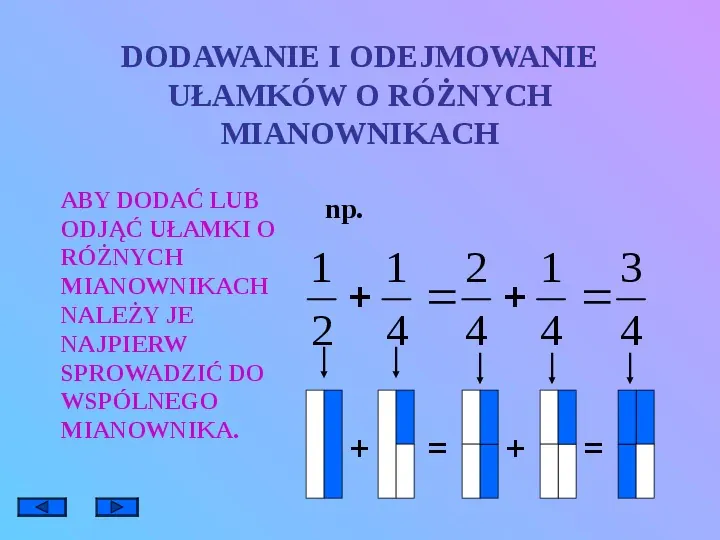
DODAWANIE I ODEJMOWANIE UŁAMKÓW O RÓŻNYCH MIANOWNIKACH ABY DODAĆ LUB ODJĄĆ UŁAMKI O RÓŻNYCH MIANOWNIKACH NALEŻY JE NAJPIERW SPROWADZIĆ DO WSPÓLNEGO MIANOWNIKA. np. 1 1 2 1 3 2 4 4 4 4

Slide 19

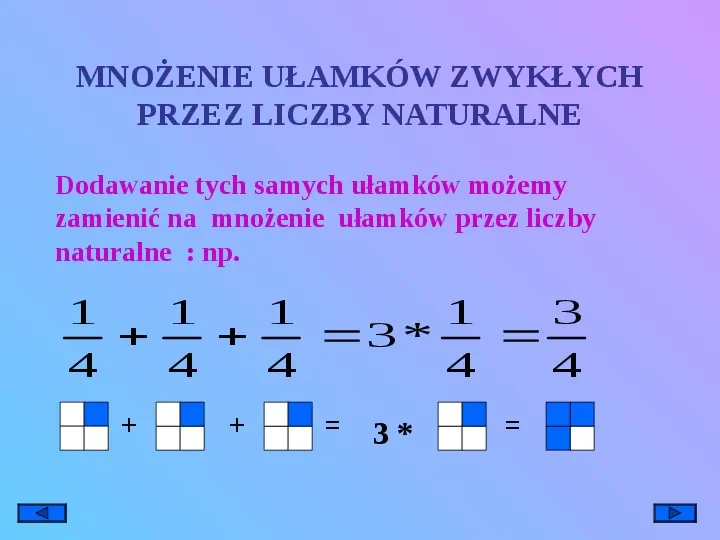
MNOŻENIE UŁAMKÓW ZWYKŁYCH PRZEZ LICZBY NATURALNE Dodawanie tych samych ułamków możemy zamienić na mnożenie ułamków przez liczby naturalne : np. 1 1 1 1 3 3 4 4 4 4 4 3

Slide 20

Aby pomnożyć ułamek zwykły przez liczbę naturalną(lub liczbę naturalną przez ułamek zwykły) należy pomnożyć licznik ułamka przez tą liczbę , a mianownik przepisać bez zmian. np. 3 3 4 12 2 4 2 5 5 5 5 Przy mnożeniu ułamków warto pamiętać o skracaniu ! np. 2 3 1 3 1 2 1 1 4 2 2 Skracamy liczbę (2) z mianownikiem( 4) przez 2 i po skreśleniu piszemy co zostało

Slide 21

MNOŻENIE UŁAMKÓW ZWYKŁYCH PRZY MNOŻENIU UŁAMKÓW ZWYKŁYCH MNOŻYMY LICZNIK PRZEZ LICZNIK UŁAMKA , A MIANOWNIK PRZEZ MIANOWNIK NP. 3 2 3 2 6 5 7 5 7 35 Przy mnożeniu ułamki możemy skracać na krzyż 1 np. 2 4 14 1 2 2 1 7 32 1 8 8 4 8 1 Należy pamiętać o tym , że nie wolno mnożyć liczb mieszanych zamieniamy je najpierw na ułamki niewłaściwe!

Slide 22

DZIELENIE UŁAMKÓW ZWYKŁYCH PRZEZ LICZBY NATURALNE Aby podzielić ułamek zwykły przez liczbę naturalną należy pomnożyć mianownik ułamka przez tą liczbę , a licznik przepisać bez zmian . :2 np. 1 2 1 4 2 2 1 1 :6 5 5 6 5 3 15 Po zamianie dzielenia na mnożenie możemy skracać licznik z mianownikiem

Slide 23

Ułamki odwrotne W ułamku odwrotnym do danego licznik staje się mianownikiem , a mianownik licznikiem . np. odwrotnością ułamka : 6 11 jest 11 6 Iloczyn ułamków (liczb) odwrotnych jest równy 1 np. 3 7 1 Aby znaleźć liczbę odwrotną do liczby mieszanej (lub całości) zamieniamy ją najpierw na ułamek niewłaściwy 7 1 3 1 32 5 23 32 ,2 1 9 9

Slide 24

DZIELENIE LICZB NATURALNYCH PRZEZ UŁAMKI ZWYKŁE ABY PODZIELIĆ LICZBĘ NATURALNĄ PRZEZ UŁAMEK ZWYKŁY NALEŻY POMNOŻYĆ TĄ LICZBĘ PRZEZ ODWROTNOŚĆ UŁAMKA np. 2 5 9 5 45 1 9 : 9 22 5 2 2 2 2 4 3 4 12 4 4 4 16 12 : 12 16 4 3 3 1 1 1

Slide 25

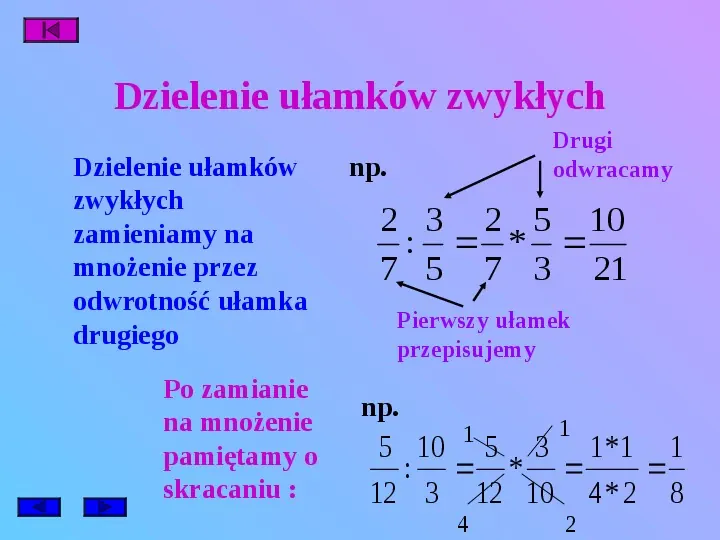
Dzielenie ułamków zwykłych Dzielenie ułamków zwykłych zamieniamy na mnożenie przez odwrotność ułamka drugiego Po zamianie na mnożenie pamiętamy o skracaniu : Drugi odwracamy np. 2 3 2 5 10 : 7 5 7 3 21 Pierwszy ułamek przepisujemy np. 1 1 4 2 5 10 5 3 1 1 1 : 12 3 12 10 4 2 8

Slide 26

UŁAMKI PIĘTROWE UŁAMKI PIĘTROWE TO UŁAMKI , KTÓRE MAJĄ WIĘCEJ NIŻ JEDNĄ KRESKĘ UŁAMKOWĄ Przykłady ułamków piętrowych: W ułamkach piętrowych zamieniamy główną kreskę ułamkową na znak dzielenia : 2 2 3,3, 9 , 5 4 11 6 9 2 21 3 4 31 2 5 2 : 3 2 7 14 3 5 7 5 3 15 7

Slide 27

OPRACOWANIE Nauczyciel matematyki Zespołu Szkół w Białce mgr DOROTA KUDZIA