Porównywanie ułamków zwykłych

Zobacz slidy

Treść prezentacji

Slide 2

Porównywanie ułamków zwykłych o jednakowych licznikach Porównywanie ułamków zwykłych o jednakowych mianownikach Rozszerzanie ułamków zwykłych Skracanie ułamków zwykłych Porównywanie ułamków zwykłych o różnych mianownikach i licznikach

Slide 4

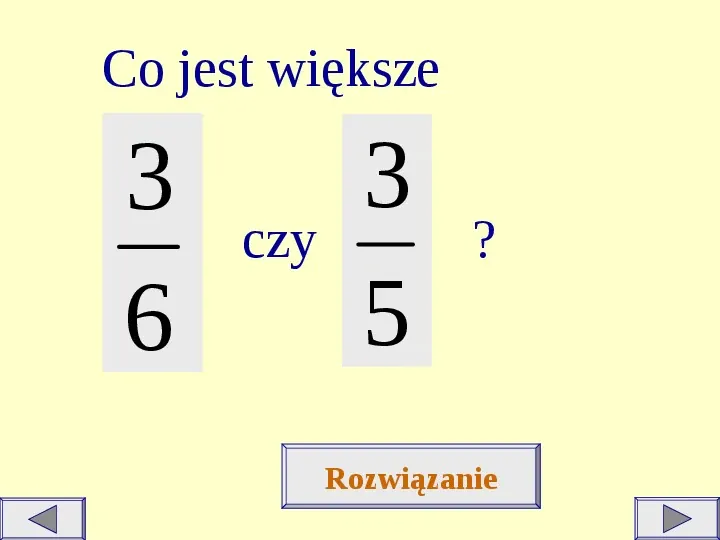
Co jest większe 3 6 czy 3 5 ? Rozwiązanie

Slide 5

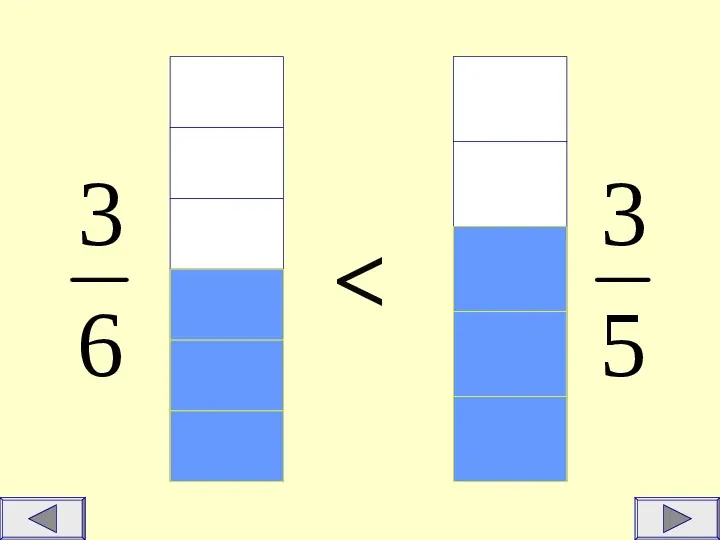
3 6 3 5

Slide 6

Spośród dwóch ułamków o jednakowych licznikach, większy jest ten, który ma mniejszy mianownik. Przykłady: 2 2 9 5 12 12 35 33

Slide 8

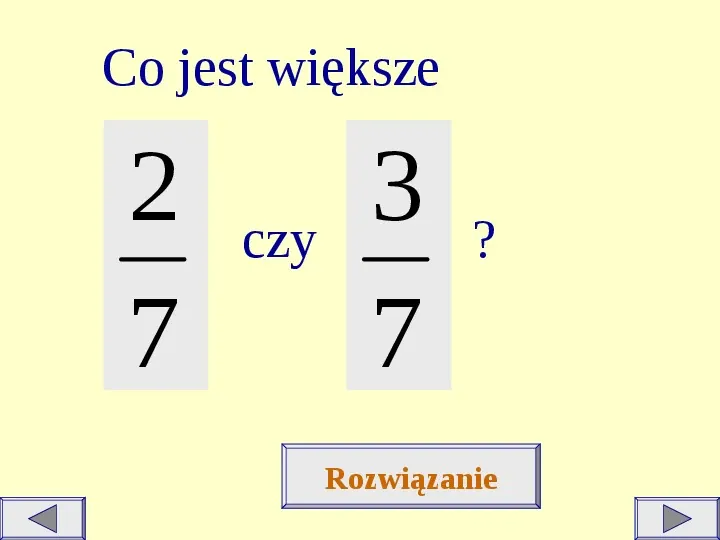
Co jest większe 2 7 czy 3 7 ? Rozwiązanie

Slide 9

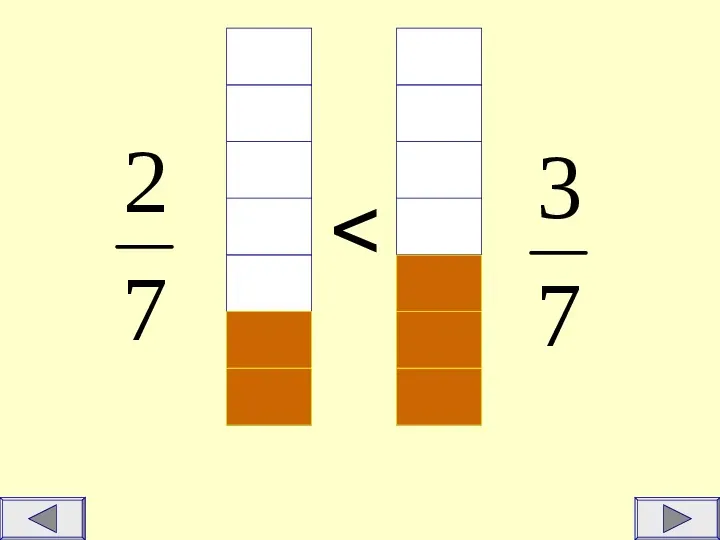
2 7 3 7

Slide 10

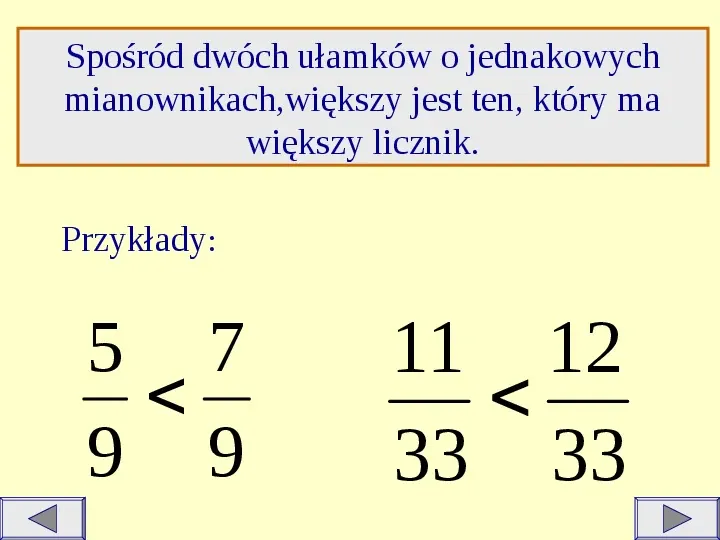
Spośród dwóch ułamków o jednakowych mianownikach,większy jest ten, który ma większy licznik. Przykłady: 5 7 9 9 11 12 33 33

Slide 12

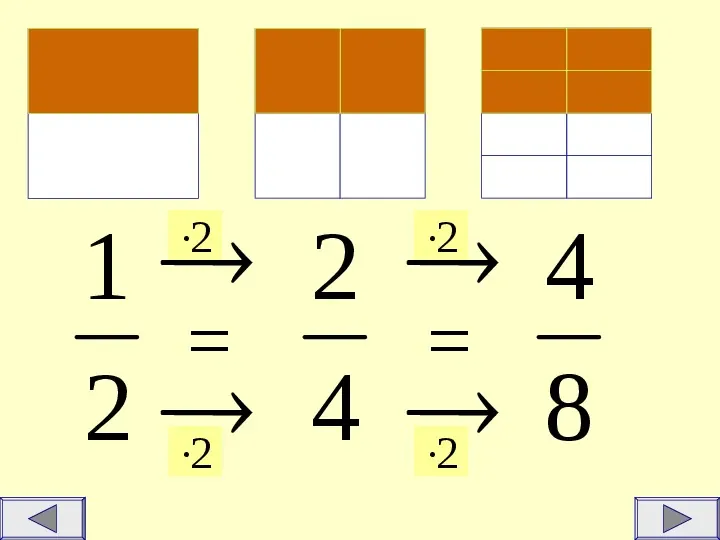
1 2 4 2 4 8 2 2 2 2

Slide 13

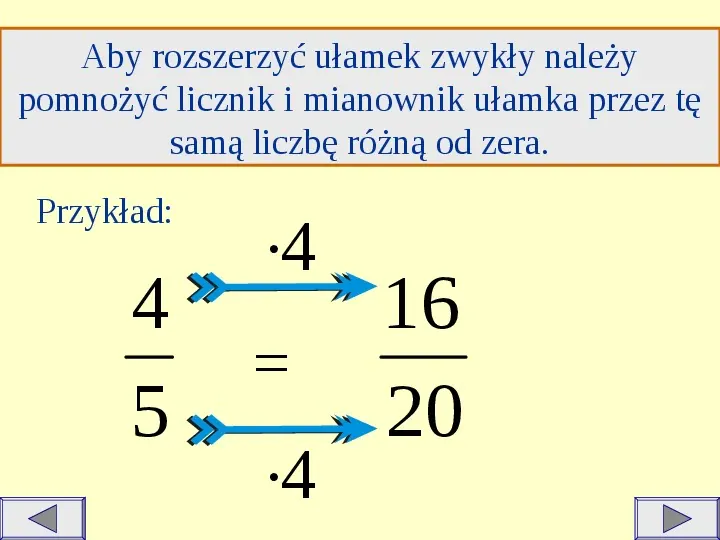
Aby rozszerzyć ułamek zwykły należy pomnożyć licznik i mianownik ułamka przez tę samą liczbę różną od zera. Przykład: 4 5 4 4 16 20

Slide 15

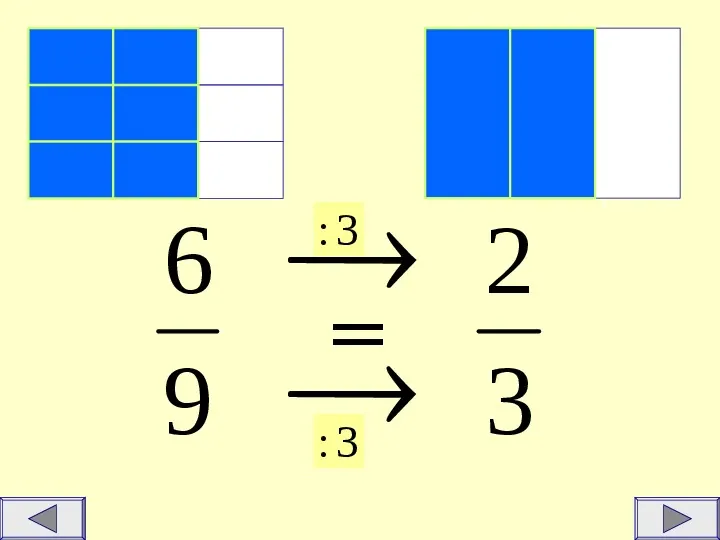
6 9 :3 :3 2 3

Slide 16

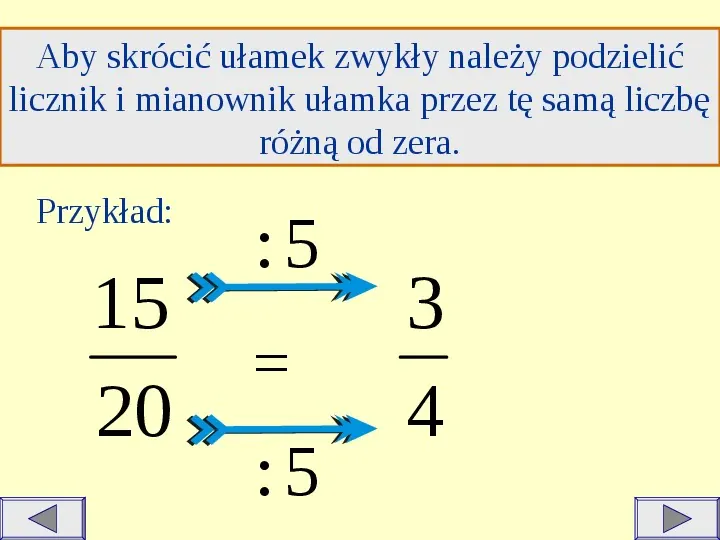
Aby skrócić ułamek zwykły należy podzielić licznik i mianownik ułamka przez tę samą liczbę różną od zera. Przykład: 15 20 :5 :5 3 4

Slide 17

UWAGA! Istnieją ułamki, których nie można skrócić. Nazywamy je ułamkami nieskracalnymi. Przykłady: 1 1 2 3 , , , 2 3 3 5

Slide 19

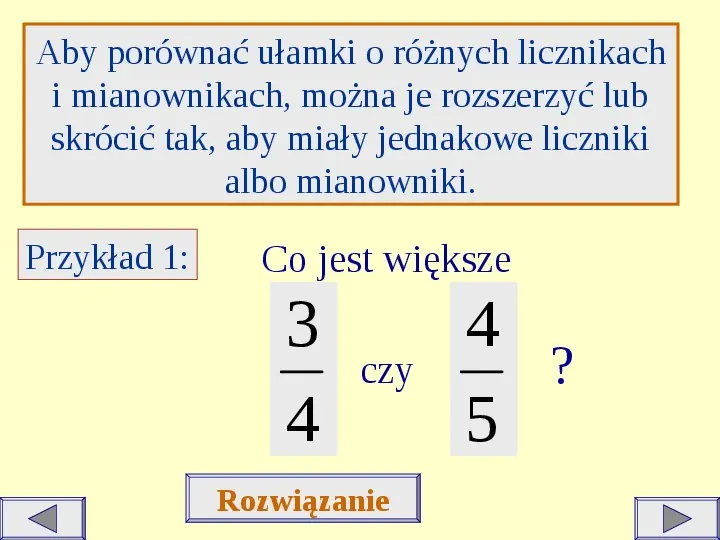
Aby porównać ułamki o różnych licznikach i mianownikach, można je rozszerzyć lub skrócić tak, aby miały jednakowe liczniki albo mianowniki. Przykład 1: Co jest większe 3 4 czy Rozwiązanie 4 ? 5

Slide 20

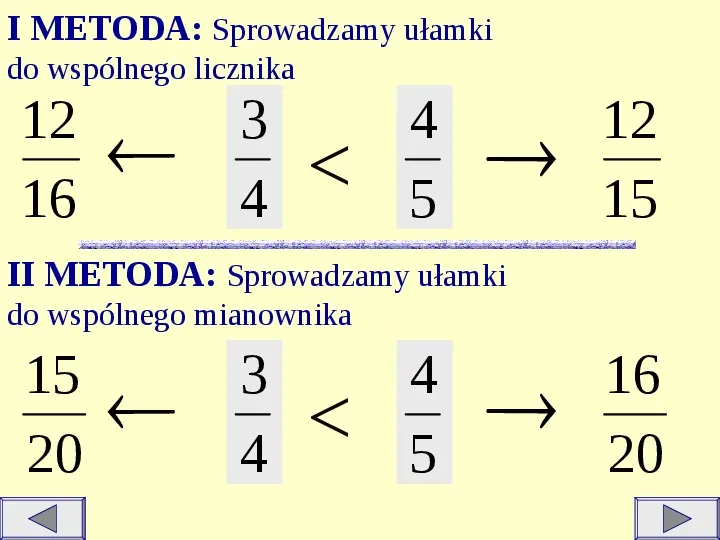
I METODA: Sprowadzamy ułamki do wspólnego licznika 12 16 3 4 4 5 12 15 II METODA: Sprowadzamy ułamki do wspólnego mianownika 15 20 3 4 4 5 16 20

Slide 21

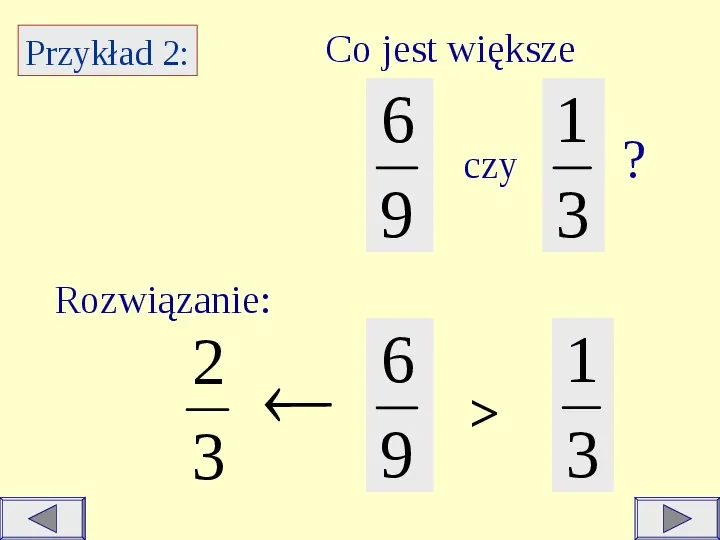
Co jest większe Przykład 2: 6 9 czy 1 ? 3 Rozwiązanie: 2 3 1 6 3 9

Slide 22

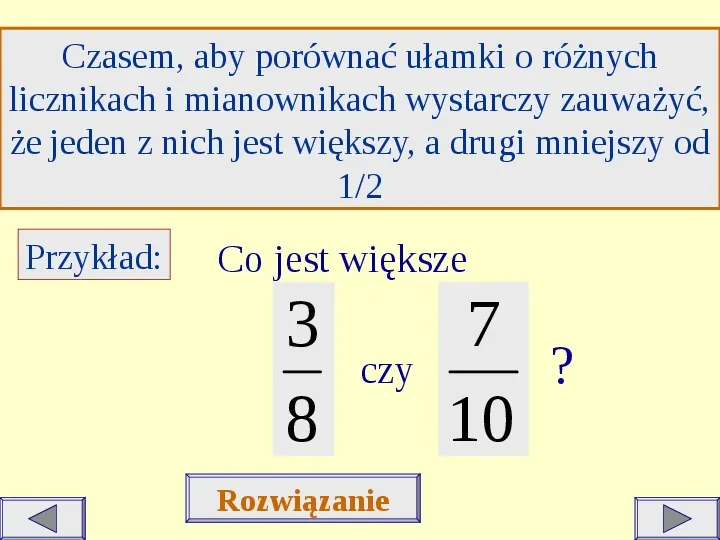
Czasem, aby porównać ułamki o różnych licznikach i mianownikach wystarczy zauważyć, że jeden z nich jest większy, a drugi mniejszy od 12 Przykład: Co jest większe 3 8 czy Rozwiązanie 7 ? 10

Slide 23

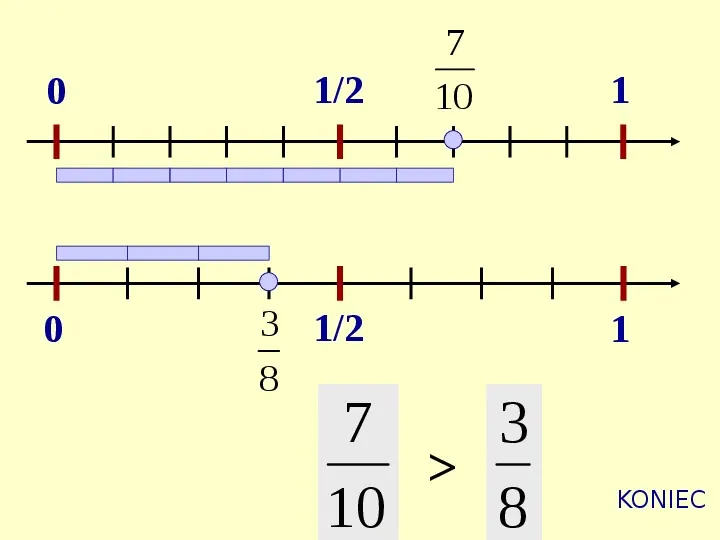
0 12 0 3 12 8 7 10 7 3 10 8 1 1 KONIEC