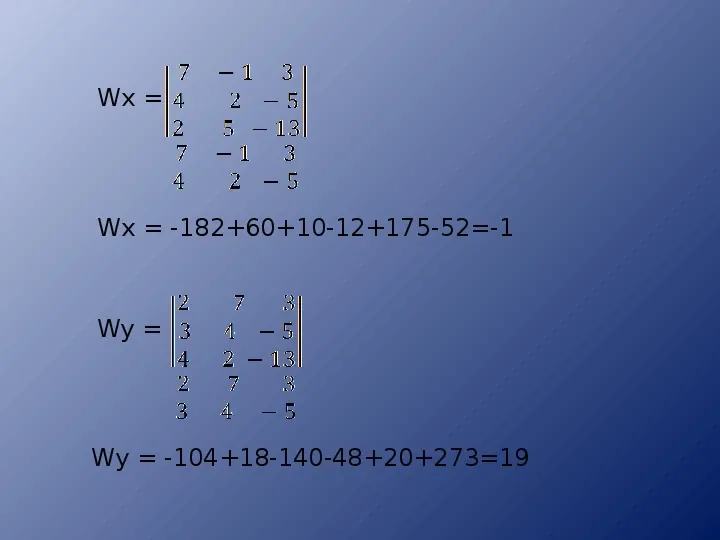Układ równań linowych z trzema niewiadomymi

Zobacz slidy

Treść prezentacji

Slide 1

UKŁADY RÓWNAŃ LINIOWYCH Z TRZEMA NIEWIADOMYMI

Slide 2

Zajmiemy się rozwiązaniem układu równań z trzema niewiadomymi. DEFINICJE: Układ równań liniowych z trzema niewiadomymi można rozwiązać stosując metodę wyznaczników: W Wx Wy Wz

Slide 3

Pod wyznacznikiem dopisujemy pierwszy wiersz, pod nim drugi wiersz, tworzymy sześć iloczynów. W Wx

Slide 4

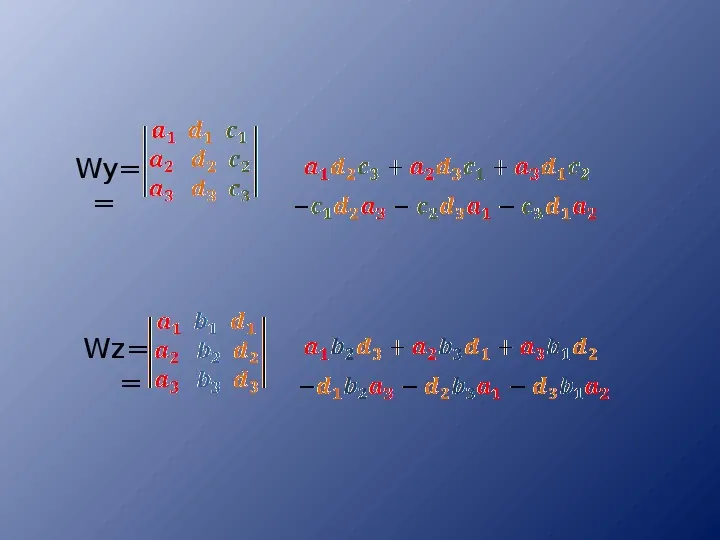
Wy Wz

Slide 5

Jeżeli: a)W 0 to trójka liczb (x,y,z) jest jedynym rozwiązaniem układu równań (równania układu są niezależne) b) W 0 to układ może nie mieć rozwiązań (równania układu są sprzeczne) albo może mieć nieskończenie wiele rozwiązań zależnych albo od jednego parametru albo od dwóch parametrów (równania układu są zależne).

Slide 6

Przykład 1. Rozwiąż układ równań: Obliczamy wyznacznik W, wyznaczniki Wx, Wy, Wz. Tworzymy kolumny z liczb znajdujących się przed odpowiedniki niewiadomymi.

Slide 7

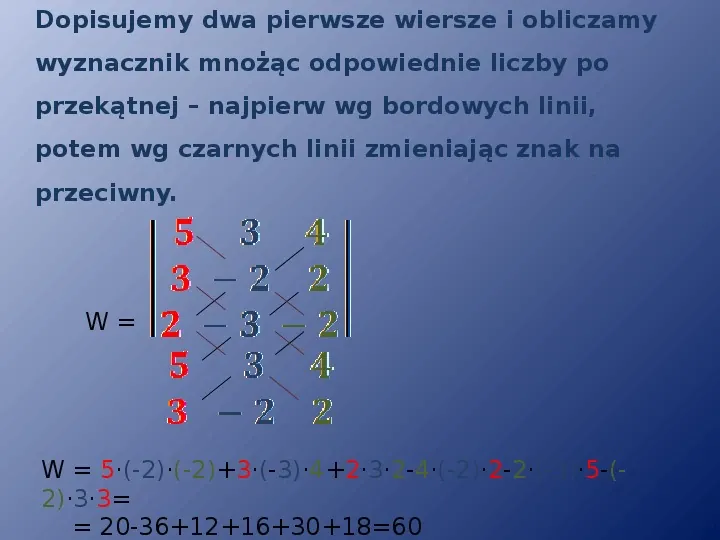
Dopisujemy dwa pierwsze wiersze i obliczamy wyznacznik mnożąc odpowiednie liczby po przekątnej najpierw wg bordowych linii, potem wg czarnych linii zmieniając znak na przeciwny. W W 5(-2)(-2)3(-3)4232-4(-2)2-2(-3)5-(2)33 20-361216301860

Slide 8

Obliczamy wyznacznik Wx tworzymy kolumnę liczb wolnych oraz kolumny liczb znajdujących się przed niewiadomą y i z. Wx Wx (-1)(-2)(-2)1(-3)4532-4(-2)5-2(-3)(-1)-(2)31 -4-123040-6654

Slide 9

Obliczamy wyznacznik Wy tworzymy kolumnę liczb wolnych oraz kolumny liczb znajdujących się przed niewiadomą x i z. Wy Wy 51(-2)3542(-1)2-412-255-(-2)(-1)3 -1060-4-8-50-6-18

Slide 10

Obliczamy wyznacznik Wz tworzymy kolumnę liczb znajdujących się przed niewiadomą x i y oraz kolumnę liczb wolnych. Wz Wz 5(-2)53(-3)(-1)231-(-1)(-2)2-1(-3)5533 -5096-415-45-69

Slide 11

Wyznacznik główny W jest różny od zera, dlatego układ równań ma jedno rozwiązanie, które obliczamy ze wzoru: Zbiorem rozwiązań układu równań jest trójka liczb:

Slide 12

Przykład 2. Metodą wyznacznikową rozwiąż układ równań: Obliczamy wyznacznik W oraz wyznaczniki: Wx, Wy, Wz W W -524520-2450-39 0

Slide 13

Wx Wx -1826010-12175-52-1 Wy Wy -10418-140-482027319

Slide 14

Wz Wz 8105-16-56-4067 Wyznacznik W ma wartość 0, wyznaczniki Wx, Wy, Wz są różne od 0. Układ równań nie posiada żadnych rozwiązań, jest sprzeczny.

Slide 15

Przykład 3 Rozwiąż układ równań: Obliczamy wyznacznik W oraz wyznaczniki: Wx, Wy, Wz

Slide 16

Wyznacznik W jest różny od 0, więc układ ma jedno rozwiązanie postaci:

Slide 17

Przykład 4. Rozwiąż układ równań: Obliczamy wyznacznik W oraz wyznaczniki: Wx, Wy, Wz

Slide 18

Wyznacznik W jest różny od 0, więc układ ma jedno rozwiązanie postaci: Zr