Historia matematyki

Zobacz slidy

Treść prezentacji

Slide 1

Czasy prehistoryczne Matematyka Egiptu i Mezopotamii Grecja starożytna Majowie Grecy Nowego Świata Średniowiecze Czasy nowożytne Matematyka XIX i XX wieku. Maszyny liczące Ciekawostki, anegdoty, humor Quiz matematyczno-historyczny Tyle jest w każdym poznaniu nauki, ile jest w nim matematyki. K.F. Gauss

Slide 2

Ludzie pierwotni mimo szybkiego tempa ewolucji dosyć powoli przyswajali sobie pojęcia matematyczne Takie pojęcia jak jeden i dwa to pojęcie bezsprzecznie najstarsze. W języku staro-greckim liczono w tenże sposób ( na przykładzie wilka). ho lykos- 1 wilk to lykos 2 wilki hoj lykos wilki

Slide 3

Za to w języku chińskim z tym problemem uporano się w następujący sposób. Słowo las przedstawiano pisząc 3 razy znak oznaczający drzewo. Słowo tłum przedstawiano 3 razy pisząc znak oznaczający człowieka.

Slide 4

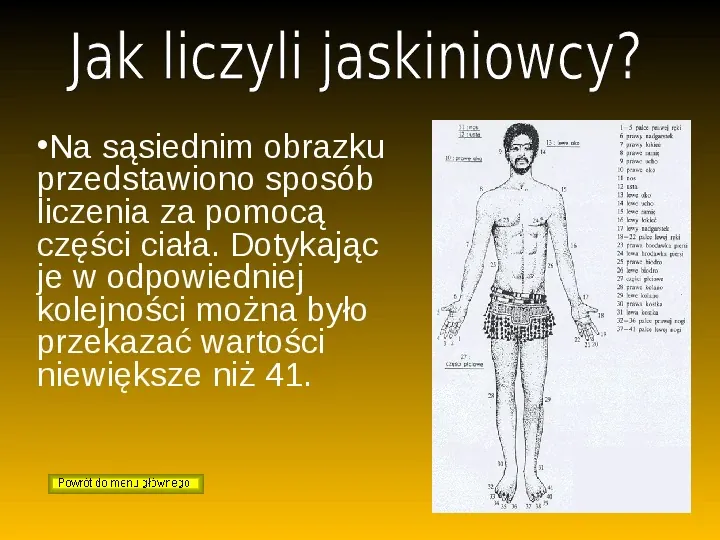
Na sąsiednim obrazku przedstawiono sposób liczenia za pomocą części ciała. Dotykając je w odpowiedniej kolejności można było przekazać wartości niewiększe niż 41.

Slide 5

Matematyka Sumerów i Babilończyków Kultury ludów znad Tygrysu i Eufratu świeciła pełnym blaskiem niemal 2000 lat przed Grekami. Również w matematyce posiadali ogromne osiągnięcie. Babilończycy posługiwali się systemem dziesiątkowym (po prawej stronie u góry) i sześćdziesiętnym ( u dołu).

Slide 6

Matematyka Sumerów i Babilończyków Umieli oni wykonywać cztery działania arytmetyczne, obliczać procenty , uznawali również ułamki. Babilończycy ułożyli między innymi tabliczkę mnożenia , stosowali w praktyce elementy twierdzenia Pitagorasa Matematyka u mieszkańców Babilonii miała znaczenie wyłącznie praktyczne.

Slide 7

Egipt Starożytny Kultura Starożytnego Egiptu podobnie jak w niedalekiej Babilonii rozwijała się już ok..3000 lat p.n.e. Również w kraju nad Nilem matematyka stała na wysokim poziomie. Matematyka w Egipcie była znana jedynie w wąskim kręgu kapłanów , którzy nierzadko wykorzystywali swe obliczenia do kontroli ciemnych mas ludności.

Slide 8

Egipt Starożytny Monumentalne dzieła starożytnych Egipcjan , takie jak chociażby piramidy w Gizie , gdyby nie obliczenia do tego niezbędne. Nieznani nam z imienia inżynierowie potrafili obliczać pola trójkątów prostokątnych ( znów 2000 lat przed Pitagorasem). Posiadali także unikalny sposób zapisywania liczb, w którym znajdowały się również i ułamki.

Slide 9

Opisując dzieje matematyki nie sposób jest zapomnieć o dokonaniach starożytnych Greków. Dzięki ich odkryciom, a także przekazaniu nam dokonań starszych cywilizacji możemy się uczyć matematyki w szkole. Poniżej opisałem pokrótce czterech , moim zdaniem, największych helleńskich matematyków Pitagoras z Samos Tales z Miletu Euklides z Megary Archimedes

Slide 10

Pitagoras był jednym z twórców tzw. Szkoły pitagorejskiej. Genialny filozof i matematyk jest nam powszechnie kojarzony z słynnym twierdzeniem , które mamy zamiar przedstawić na kolejnej stronie Pitagoras był nie tylko wybitnym matematykiem ale również filozofem i twórcą własnego systemu wierzeń i zagadnień etycznych

Slide 11

Matematyk z Samos był nie tylko autorem jednego twierdzenia. Wraz z uczniami założonego przez siebie zakonu odkrył wiele prawideł geometrii , stworzył również trzy wielki problemy geometryczne , takie jak podwojenie sześcianu , kwadratura koła i podział kąta na trzy części.

Slide 12

Twierdzenie Pitagorasa: W trójkącie prostokątnym, suma kwadratów przyprostokątnych jest równa kwadratowi przeciwprostokątnej. c a b 2 2 a b c 2

Slide 13

Euklides z Megary jako pierwszy uporządkował zasady tworzące w starożytności geometrię, Jego dzieło Elementy , spisane w 13 księgach stało się najczęściej wydawanym i studiowanym dziełem kultury zachodniej. Od chwili powstania druku ukazało się ponad 1000 wydań. Geometria której obecnie uczymy się w szkole, jest niemal w całości, geometrią euklidesową.

Slide 14

Elementy oprócz teorii geometrycznych zawierają również teorię liczb Euklides pisał również pracę dotyczące również astronomii, optyki, pedagogiki i muzyki.

Slide 15

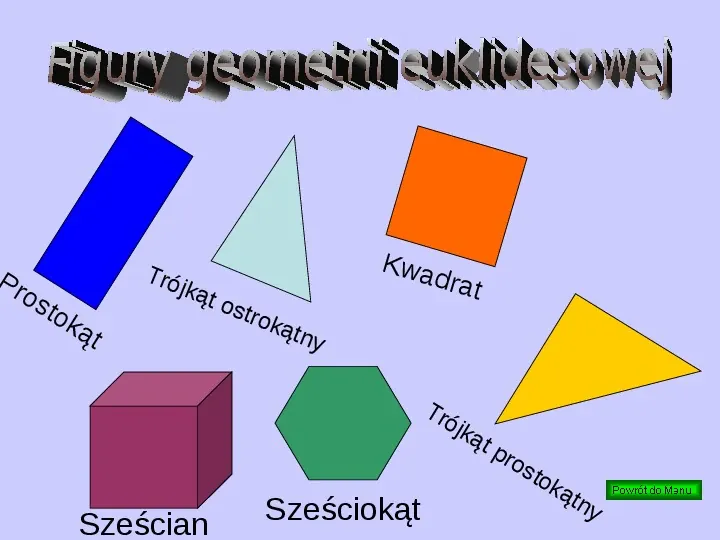
Pr os tok ąt Tró jkąt ost rok ątn y Sześcian Kwa drat Sześciokąt Tró jką tp ros tok ątn y

Slide 16

Tales jest uznawany za ojca nauki greckiej. Już przez starożytnych uważany był za pierwszego z filozofów, matematyków, fizyków i astronomów. Jako mieszkaniec nadmorskiego Miletu , aktywnie uczestniczył w życiu politycznym i gospodarczym. Utrzymywał kontakty zarówno z Babilonią jak i Egiptem , gdzie dzięki licznym podróżom zapoznał się z matematyką i astronomią.

Slide 17

Tales dzięki obliczeniom matematycznym obliczył dokładnie czas zachodu słońca (28 V 585 r .p.n.e. ) , a w czasie wojaży w Egipcie zdołał obliczyć na podstawie cienia dokładną wysokość piramid w Gizie. Około 160 lat po śmierci , Platon napisał o nim anegdotę o tym że w czasie obserwacji astronomicznych tak zapatrzył się w gwiazdy, że wpadł do studni. Piękna niewolnica Talesa miała wyrazić się żartem że mieszkaniec Miletu zapatrzył się w gwiazdy a zapomniał o tym co na ziemi.

Slide 18

Jeśli ramiona kąta przeciąć dwiema równoległymi, to długości odcinków wyznaczonych przez te proste na jednym ramieniu kąta są proporcjonalne do długości odpowiednich odcinków na drugim ramieniu kąta.

Slide 19

Archimedes (287-212 p.n.e.) Archimedes urodził się w Syrakuzach. Pierwsze nauki pobierał u swego ojca Fidiasza , następnie studiował w Aleksandrii. Współdziałał tam z Eratostenesem. Niektórzy twierdzą iż pomagał mu w obliczeniu obwodu kuli ziemskiej O dziełach słynnego fizyka i matematyka krążą legendy. Już starożytni twierdzili że są trudne , wręcz niezrozumiałe. Archimedes liczył zapewne na dojrzałość odbiorcy. Mimo wszystko jego prace były intensywnie tłumaczone najpierw przez Arabów , później przez Europejczyków.

Slide 20

Archimedes (287-212 p.n.e.) W odróżnieniu od żyjącego wcześniej Euklidesa , był autorem prac wnoszących dużo więcej do dotychczasowej wiedzy , nie poprzestawał na systematyzacji Po prawej stronie monitora jest przedstawiony jest rysunek dotyczący jednego z prawideł odkrytych przez Syrakuzańczyka.

Slide 21

Pisząc o Archimedesie nie sposób jest zapomnieć o anegdocie dotyczącej odkrycia prawa wyporu. Podczas kąpieli w wannie w czasie której sprawdzał on czy wykonana przez złotnika korona dla tyrana Syrakuz jest całkowicie złota , matematyk po jakimś czasie wyskoczył z niej krzycząc słynne Eureka! Nie wspominając o tym że jakiś czas później zaczął biegać po ulicach, goły. Na każde ciało zanurzone w cieczy działa siła wyporu , jej wartość jest równa wartości ciężaru cieczy wypartego przez to ciało

Slide 22

Majowie Grecy Nowego Świata Przydomek Greków Nowego Świata należy się Majom nieprzypadkowo. Mieszkańcy półwyspu Jukatan prawdopodobnie jako jedyni mieszkańcy obydwu Ameryk wynaleźli system numeryczny o poziomie dorównującym Europejczykom i Azjatom. Majowie znani są również ze swojego kalendarza. Posiadali więc również sprecyzowaną rachubę czasu.

Slide 23

Majowie Grecy Nowego Świata Majowie jako druga nacja ( po Sumerach) uznała wartość 0 , przedstawiając ją w formie otwartego do połowy oka. Plemię z południowego Meksyku dzięki doskonałej znajomości matematyki zdołało zbudować piramidy , świątynie ( do nieomal 60 metrów) , nie posiadając narzędzi pomiarowych 0 1 5 10

Slide 24

Renesans europejski dotyczył nie tylko prądów kulturalnych ale również nauk ścisłych. Nastąpił powrót do źródeł antycznych , ale nie kopiowano tylko wzorów i teorii starożytnych lecz wykorzystywano je do konstruowania własnych twierdzeń. Za jedną z najwybitniejszych postaci odrodzenia należy uznać Leonarda z Pizy (Fibonaccia). Żyjący na przełomie średniowiecza i odrodzenia matematyk sprowadził i zaczął używać cyfr arabskich. Jako pierwszy Europejczyk uznał istnienie liczb ujemnych.

Slide 25

W średniowieczu matematykę uprawiali gł. uczeni arab., którzy rozpowszechnili w Europie stworzony przez Hindusów pozycyjny (dziesiątkowy) system liczenia i rozwijali algebrę, której początki wiążą się m.in. z pracami matematyka arab. AlChuwarizmiego (IX w.). Liczby

Slide 26

Z liczbami ujemnymi wiąże się pewna historia. Otóż w czasie turnieju matematycznego Leonardo nie pominął milczeniem istnienia liczbv ujemnej ale zdołał ją wytłumaczyć poglądowo , jako dług. Wspominając o renesansie , nie sposób zapomnieć o geniuszu tej skali co Leonardo da Vinci. Zajmował się on dziełami starożytnych matematyków greckich , pisał również pracę dotyczące geometrii.

Slide 27

Wiek XVI charakteryzuje przedłużenie osiągnięć renesansu. Do najwybitniejszych przedstawicieli matematyki w tym czasie należy zaliczyć G. Cardano, N. Taraglia i L. Ferrari którzy stworzyli metody rozwiązywania równań III i IV stopnia. Za początek nowoczesnej matematyki należy uznać wiek XVII. W tym czasie działali tacy uczeni jak Kartezjusz , Leibniz , Fermat , Pascal czy Newton . Narodziły się metody rachunku różniczkowego i całkowego , a także geometria analityczna.

Slide 28

Wiek XVIII , czyli Oświecenie , to okres działania przede wszystkim szwajcarskiego kalkulatora czyli L.Eulera. Ów matematyk wywarł ogromny wpływ na nowoczesną matematykę , dzięki niemu rozwinięta została analiza matematyczna i geometria analityczna. Przykład elementu geometrii analitycznej: Funkcja kwadratowa: y x 2

Slide 29

Kartezjusz żył w latach 15961650. Jest on uważany za twórcę nowożytnej kultury umysłowej. Zajmował się m.in. matematyką, optyką, chemią, mechaniką, anatomią, embriologią, medycyną, astronomią i meteorologią. Zaliczany jest również do najwybitniejszych myślicieli filozofów swoich czasów.

Slide 30

Kartezjusz jest autorem słynnej maksymy cogito ergo sum myślę więc jestem. Filozof podawał w wątpliwość doznania zmysłowe , a za jedyny fakt świadczący o samoświadomości uznawał samodzielne myślenie. Jeśli chodzi o dokonania matematyczne , Rene Descartes w dzieje tej nauki włożył wielki wkład. To on jako pierwszy użył terminu funkcja , stworzył również podstawy geometrii analitycznej oraz rachunku różniczkowego i całkowego

Slide 31

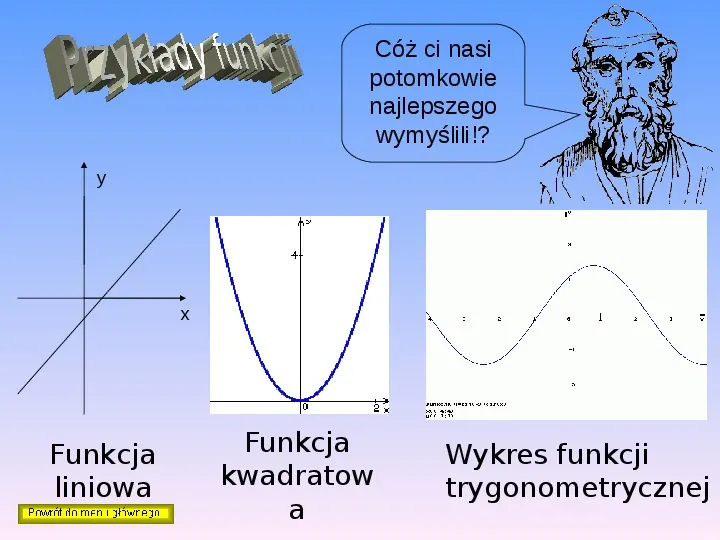
Cóż ci nasi potomkowie najlepszego wymyślili!? y x Funkcja liniowa Funkcja kwadratow a Wykres funkcji trygonometrycznej

Slide 32

Koniec XIX wieku był początkiem rozwoju urządzeń mechanograficznych, których głównym przeznaczeniem było usprawnienie rachunków statystycznych, księgowych i biurowych. Zaczęło się W USA od Hermana Holleritha, ktry postanowił zautomatyzować prace statystyczne związane ze spisem ludności przeprowadzanym wtedy w Stanach co 10 lat. Hollerith wykorzystał elektryczność jako źródło impulsów i energii, rozwinął postać karty perforowanej, na której zapisywano dane i zbudowano elektryczny czytnik kart.

Slide 33

Olbrzymim sukcesem Holleritha okazał się spis w 1890 roku, którego wyniki zostały całkowicie opracowane za pomocą jego urządzeń na podstawie danych zebranych na jego kartach. N a przełomie XIX i XX wieku powstało wiele firm, które oferowały maszyny sterowane kartami perforowanymi. Wiele z nich przetrwało do dzisiaj, jak na przykład IBM, Bull, Remington-Rand, Burroughs, NCR czy Bell.

Slide 34

Od prostych liczydeł po Nowoczesne komputery

Slide 35

Urządzeniami do wspomagania obliczeń matematycznych, przetwarzania informacji zajmowano od wieków. Jednym z najstarszych urządzeń do przetwarzania informacji był abak, używany przez starożytnych Egipcjan, Greków i Rzymian.

Slide 36

W 1614r. matematyk szkocki John Neper wynalazł logarytmy oraz zastosował pałeczki (od jego nazwiska nazwano pałeczkami Nepera), pozwalające na znaczne przyspieszenie żmudnych obliczeń. Wynalazek Nepera zapoczątkował rozwój urządzeń analogowych służących do liczenia.

Slide 37

Pierwszym znanym cyfrowym mechanicznym urządzeniem liczącym była czterodziałaniowa maszyna licząca, zaprojektowana przez niemieckiego astronoma i matematyka W. Schickharda. W 1643r. Blaise Pascal francuski matematyk zbudował dwudziestodziałaniową maszynę do liczenia. Był to pierwszy krok w kierunku automatyzacji urządzeń liczących.

Slide 38

W 1882 roku Charles Babbage angielski matematyk zaprojektował i częsciowo skonstruował maszynę licząca metodą różnic skończonych.

Slide 39

W 1833 opracował projekt maszyny analitycznej działającej na zasadzie zbliżonej do zasady działania współczesnych komputerów, nazwanej młynkiem arytmetycznym. Miała wykonywać podstawowe działania matematyczne, zapamiętywać dane wejściowe, pośrednie oraz wyniki obliczeń. Wprowadzaniu i wyprowadzaniu danych służyły karty dziurkowane. Projekt nie doczekał się realizacji z powodu niskiego poziomu ówczesnej techniki.

Slide 40

W 1946r. w USA zbudowano maszynę liczącą, do której budowy użyto lamp elektronowych. Maszynę nazwano ENIAC skrót od Elektronic Numerical Integrator and Computer. Twórcami urządzenia byli John Presper Eckert i John Mauchly z Moore School of Electrical Engineering (University of Pennsylvania).

Slide 41

ENIAC był elektronicznym sumatorem i kalkulatorem cyfrowym. Zawierał 18 tysięcy lamp elektronowych. Ważył 30 ton. Pamięć mieściła 20 liczb dwudziestocyfrowych. Maszynę wykorzystywano między innymi do obliczeń balistycznych. ENIAC wykonywał 5000 dodawań na 1s.

Slide 42

Wśród modeli obliczeń powstałych w pierwszej połowie XX wieku największą popularność zdobyły maszyny Turinga. W swojej fundamentalnej pracy z 1936 roku Alan Turing bardzo przystępnie opisał tok myślenia prowadzący od obliczeń wykonywanych ręcznie do obliczeń wykonywanych przez bardzo prostą maszynę.

Slide 43

Prace Turinga miały ogromne znaczenie dla rozwoju informatyki i maszyn liczących. Pierwsze komputery zbudowano dopiero w XX wieku, chociaż pomysły, jakie w nich zrealizowano, pojawiły się około sto lat wcześniej, już za czasów Babbagea. Zastosowane w komputerach środki techniczne pojawiły się dopiero w latach międzywojennych. Za największego inspiratora powstania komputera w jego obecnej postaci uważa się Johna von Neumanna Zaproponował on architekturę, zwaną odtąd von neumannowską, według której buduje się komputery do dnia dzisiejszego... Co byście zrobili bez nas?

Slide 44

Jeśli graniastosłup sześciokątny podzielimy wzdłuż przekątnej podstawy, to otrzymamy dwie trumny. Trójkąt Pitagorasa, to trójkąt kwadratowy. Suma to nie wynik dodawania, tylko msza rano w niedzielę. Koło to jest linia, bez kątów, zamknięta, by nie było wiadomo gdzie jest początek. Trójkąt równoramienny ma równe ramiona, jednak jeden z boków jest krótszy.

Slide 45

Całka całki to jak córka córki czyli wnuczka. Linijka, kątomierz i cyrkiel to narządy matematyczne. W życiu Pitagorasa liczyło się tylko liczydło oraz kalkulator, którego wtedy jeszcze nie znano. Linijka 20 centymetrowa ma ponad 20 centymetrów. Prostokąt rożni się od kwadratu tym, że raz jest wyższy a raz szerszy. Pierwszy człowiek na ziemi nie czuł się samotny bo nie umiał liczyć.

Slide 46

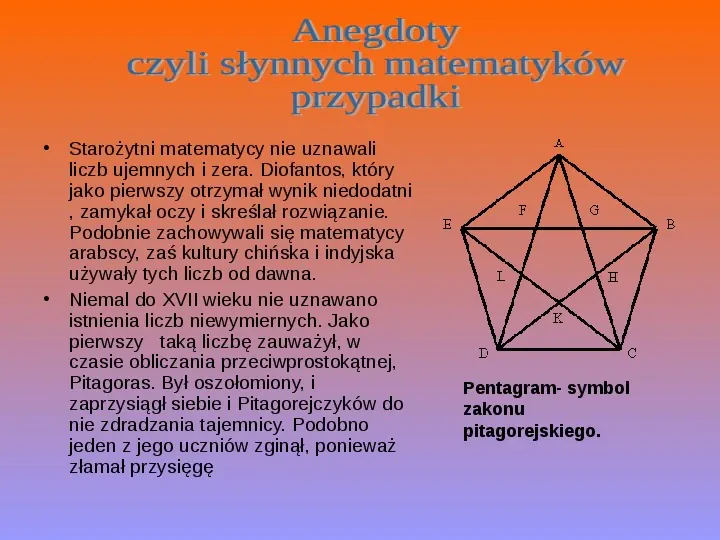
Starożytni matematycy nie uznawali liczb ujemnych i zera. Diofantos, który jako pierwszy otrzymał wynik niedodatni , zamykał oczy i skreślał rozwiązanie. Podobnie zachowywali się matematycy arabscy, zaś kultury chińska i indyjska używały tych liczb od dawna. Niemal do XVII wieku nie uznawano istnienia liczb niewymiernych. Jako pierwszy taką liczbę zauważył, w czasie obliczania przeciwprostokątnej, Pitagoras. Był oszołomiony, i zaprzysiągł siebie i Pitagorejczyków do nie zdradzania tajemnicy. Podobno jeden z jego uczniów zginął, ponieważ złamał przysięgę Pentagram- symbol zakonu pitagorejskiego.

Slide 47

Bardzo ciekawa anegdota wiąże się z słynnym matematykiem z Syrakuz. Otóż Archimedes, w czasie szturmu Rzymian na Syrakuzy, wykonywał nadal obliczenia. Gdy napotkał go jeden z szturmujących , poprosił go aby nie niszczył jego rysunku Sto lat później Cyceron pisał, że w czasie wędrówek po Sycylii napotkał grób z walcem opisanym na kuli. Okazało się że odnalazł grób wybitnego matematyka , Archimedesa

Slide 48

Co myślisz Pitagorasie o umieszczeniu na mym grobie walca opisanego na kuli? Dobrze że nie próbowałeś rysować kwadratury koła

Slide 49

Każdy z nas zapewne słyszał o Isaacu Newtonie. Słynny angielski fizyk również był człowiekiem i cierpiał bardzo z powodów psychicznych. Był on samotnikiem, nielicznych swych przyjaciół traktował chłodno i był wobec nich niemiły. Nierzadko zdarzało się że na jego wykłady nie przychodził nikt. W tym przypadku nie opuszczał wykładów, przemawiając do pustej sali.

Slide 50

L.Euler, szwajcarski matematyk, prekursor analizy matematycznej, w ostatnich latach życia cierpiał na ślepotę. W owym czasie mieszkał na dworze carycy Katarzyny. Do ostatnich lat życia wykonywał skomplikowane obliczenia matematyczne, wykonując je w głowie A.Einstein, jeden z najwybitniejszych uczonych w historii cierpiał w liceum na powód dosyć prozaiczny. Miał problemy z matematyką (z której miał zresztą dwóję). W latach dziecięcych był samotny, nie potrafił nawiązać prostego kontaktu z rówieśnikami.

Slide 51

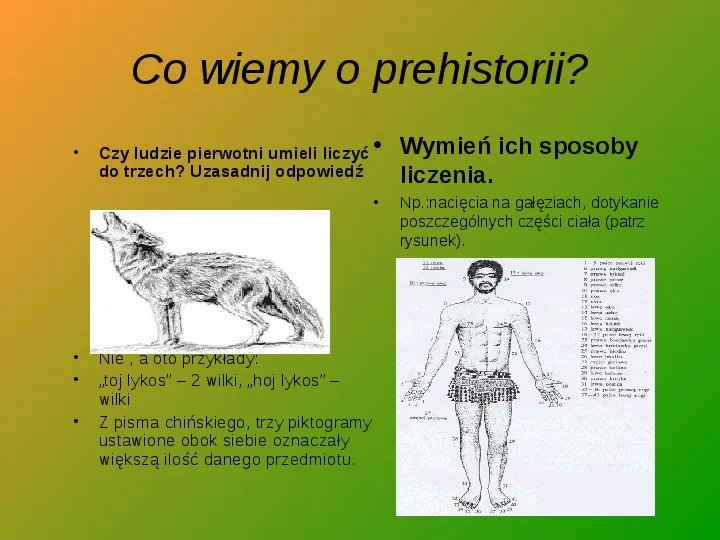
Co wiemy o prehistorii? Czy ludzie pierwotni umieli liczyć do trzech? Uzasadnij odpowiedź Nie , a oto przykłady: toj lykos 2 wilki, hoj lykos wilki Z pisma chińskiego, trzy piktogramy ustawione obok siebie oznaczały większą ilość danego przedmiotu. Wymień ich sposoby liczenia. Np.:nacięcia na gałęziach, dotykanie poszczególnych części ciała (patrz rysunek).

Slide 52

Egipt i Babilonia Jakim systemem liczenia posługiwali się Babilończycy. a) Dziesiątkowym b) Sześćdziesiątkowym c) Babilońskim Do skomplikowanych obliczeń używali tzw. systemu sześć dziesiątkowego. Jakie wielkie budowle powstały w Egipcie dzięki znajomości geometrii? M.in. Piramidy w Gizie.

Slide 53

Grecja starożytna. Który matematyk przysporzył nam najwięcej kłopotów odkrywając trzy wielkie problemy geometryczne? a) Tales z Miletu b) Pitagoras z Samos c) Eratostenes Jaki wielki fizyk w czasie kąpieli wyskoczył z wanny i , goły, zaczął przemierzać ulicę rodzinnego miasta? Archimedes! A te problemy to : podwojenie sześcianu , podział kąta na trzy części i kwadratura koła.

Slide 54

Średniowiecze Kto sprowadził liczby arabskie do Europy? a) Leonardo da Vinci b) Fibonaccio (Leonardo z Pizy) c) Cardano Kto odkrył 0 i liczby ujemne? a) b) c) Europejczycy Arabowie Hindusi

Slide 55

Początek nowoczesnej matematyki Który z matematyków stworzył prostokątny układ współrzędnych? a) Rene Descartes b) Conrad Gauss c) Immanuel Kant To ja! Który matematyk XVIII w. Był nazywany szwajcarskim kalkulatorem a) P.Fermat b) B.Pascal c) L.Euler

Slide 56

Maszyny liczące! W 1643r. Blaise Pascal francuski matematyk zbudował: a) czterodziałaniowa maszynę licząca b) maszynę licząca metodą różnic skończonych c) dwudziestodziałaniową maszynę do liczenia Kto zaproponował architekturę, według której buduje się komputery do dnia dzisiejszego? a) John von Neumanna b) Alan Turing c) John Mauchly