Sposoby zapisywania liczb

Zobacz slidy

Treść prezentacji

Slide 1

Sposoby zapisywania liczb Autorzy: Kinga Górska Małgorzata Obara

Slide 2

W rozwoju kultury ludzkiej pierwsze pojawiły się liczby naturalne. Systemy pozycyjne pojawiły się w I tysiącleciu przed naszą erą w starożytnej Babilonii, w pierwszych latach naszej ery u Majów, przed IX wiekiem naszej ery w Indiach, skąd system dziesiątkowy przejęli Arabowie, a od nich Europejczycy. Znaki, za pomocą których zapisujemy liczby to cyfry. Używamy 10 cyfr. Są to: 1, 2, 3, 4, 5, 6, 7, 8, 9 i 0. Wyraz cyfra pochodzi od arabskiego wyrazu sifr, oznaczającego zero. Zostało ono zaczerpnięte od Hindusów. Wiadomo, że zera używał induski uczony Arjabhata, którego dzieło pt. ,,Surjasiddhanta w zachowanej swej postaci sięga wieku V. Uczony użył tam terminu ,,siunia, który oznacza pustkę, zero. Zero było zapisywane początkowo jako punkt. Jeszcze dziś w Turcji, Egipcie i krajach Bliskiego Wschodu zero zapisuje się w kształcie kropki czworokątnej, a piątkę w kształcie zera. Najstarsze dokumenty zawierające znaki liczb sięgają IV wieku p.n.e.

Slide 3

System liczb, których używamy obecnie, wynaleźli Hindusi. Europejczycy poznali go jednak za pośrednictwem Arabów, dlatego mówimy o cyfrach arabskich. Dawniej w Europie nie pisano liczb, tak jak dziś. Najstarszy znany europejski rękopis, w którym spotykamy cyfry arabskie (bez zera) był pisany w Hiszpanii w 976 roku. W rękopisach arabskich cyfry te spotykamy już sto lat wcześniej. W 1202 roku włoski kupiec z Pizy, Leonardo Fibonacci wydał książkę o abakusie pt. ,,Liber Abaci, w której wykazywał zalety zapisywania liczb w układzie powstałym przez dołączenie znaku zero do znanych już cyfr. System ten jednak długo rozpowszechniał się w Europie, bo np. pierwsze monety z cyframi hinduskimi pojawiły się w Szwajcarii w 1424 roku, w Austrii w 1484 roku, we Francji w 1485 roku, w Niemczech w 1489 roku, w Polsce w 1506 roku, w Anglii w 1551 roku, w Rosji w1655 roku.

Slide 4

Były dwa typy cyfr: typ hindi i typ gubari. Arabowie używali na wschodzie cyfr typu hindi, a na zachodzie cyfr typu gubari. Cyfry, którymi posługują się m.in. Europejczycy są typu gubari, natomiast u Arabów i ludów posługujących się pismem arabskim zachował się typ hindi. Cyfry arabskie zmieniały swoją postać. W różnych okresach wyglądały bardzo odmiennie od obecnych.

Slide 5

LICZBY SUMERÓW Sumerowie był to lud zamieszkujący w IV wieku p.n.e. dolny Eufrat (teren dzisiejszego Iraku). Lud ten pisał półokrągłym, a później trójgraniastym rylcem na płytkach drewnianych, kamiennych, a najczęściej glinianych, które wypalane przetrwały do naszych czasów. Sumerowie zapisywali liczbę 1 znakiem pionowego klina . Za jego pomocą zapisywali liczby od 1 do 9, grupując je w rzędach obok lub zapisując jedne nad drugimi. Do oznaczania liczby 10 stosowali znak składający się z dwóch pionowych klinów połączonych razem i tworzących kąt . Powtarzając wymienione znaki i grupując je zapisywali liczby od 1 do 99, przy czym dziesiątki zapisywali na lewo od jedności. Np. układ znaków oznacza liczbę 23.

Slide 6

Liczbę 100 Sumerowie oznaczali znakiem powstałym z połączenia dwóch klinów: pionowego i poziomego: . Liczbę 1000 zapisywali umieszczając znak 10 przed 100, co oznaczało mnożenie liczby 10 przez 100. Ponowne umieszczenie znaku liczby 10 przed znakiem liczby 1000 oznaczało 10 x 100010 000.

Slide 7

W wysoko rozwiniętej cywilizacji Starożytnego Egiptu także pojawiły się znaki przedstawiające liczby. Znane są trzy rodzaje zapisów: hieroglify, znaki hieratyczne i demotyczne. Hieroglify można odnaleźć choćby na pomniku pochodzącym z około 3300 lat p.n.e., wystawionym dla uczczenia zwycięstwa, na którym zanotowano liczbę jeńców i liczbę sztuk zdobytych zwierząt. Pismo hieratyczne można zobaczyć na tzw. papirusie Ahmesa, znalezionym w Tebach (obecny Luksor), który dziś znajduje się w Muzeum Brytyjskim w Londynie. hieroglify

Slide 8

Hieratyczne znaki liczb Demotyczne znaki liczb

Slide 9

W Grecji pierwotny sposób zapisu liczb, pochodzący z VI wieku p.n.e., polegał na zapisywaniu początkowych liter nazw liczb zamiast tych liczb. W tabeli prezentujemy przykładowe liczby greckie: Liczba 5 10 100 1000 10 000 Zapis grecki czytamy pi delta hekto chi miriada Dodatkowe znaki utworzono za pomocą łączenia znaku 5 oraz jednego z pozostałych znaków, przy czym znak 5 przybierał najczęściej kształt uproszczony . Używano poza tym znaków: oraz jako 50 000. jako 50, jako 500, jako 5000

Slide 10

Liczbę 1 zapisywano jako pionową kreskę. Razem wszystkich znaków było więc 10; za ich pomocą zapisywano wszystkie liczby. Aby zapisać liczbę, np.67837,umieszczano kolejno od lewej strony do prawej znaki liczb (razem było ich 15). Trudno uważać taki zapis za wygodny. W attyckich napisach używano tych znaków liczbowych przez przeszło 400 lat, aż do I wieku p.n.e. Nieco późniejszy sposób zapisu pochodzi z miasta Milet. Sposób ten polegał na wykorzystaniu wszystkich liter alfabetu greckiego oraz trzech liter semickich jako znaków liczb. Początkowe osiem kolejnych liter alfabetu greckiego wraz ze wstawioną na szóstym miejscu literą digamma oznaczały kolejno 1,2,39, tzn: Cyfra 1 2 3 4 5 6 7 8 9 Znak grecki alfa beta gamma delta epsilon digamma dzeta eta theta Czytam y

Slide 11

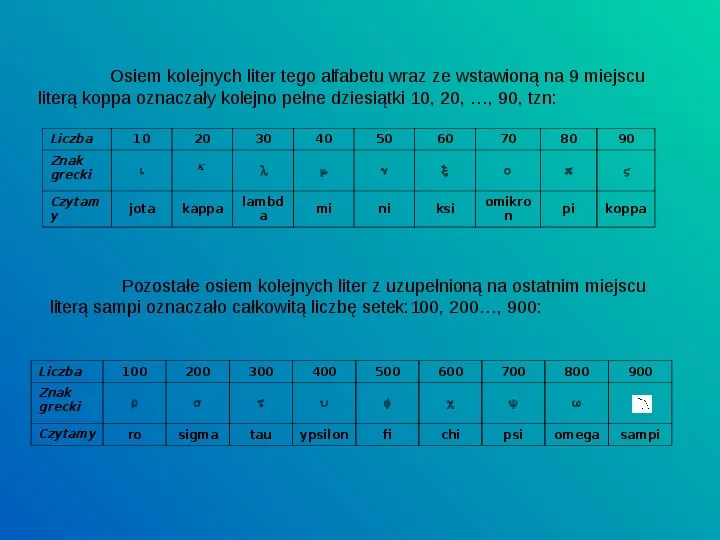
Osiem kolejnych liter tego alfabetu wraz ze wstawioną na 9 miejscu literą koppa oznaczały kolejno pełne dziesiątki 10, 20, , 90, tzn: Liczba 10 20 30 40 50 60 70 80 90 Znak grecki jota kappa lambd a mi ni ksi omikro n pi koppa Czytam y Pozostałe osiem kolejnych liter z uzupełnioną na ostatnim miejscu literą sampi oznaczało całkowitą liczbę setek:100, 200, 900: Liczba 100 200 300 400 500 600 700 800 Znak grecki Czytamy ro sigma tau ypsilon f chi psi omega 900 sampi

Slide 12

Cyfry rzymskie to cyfry pochodzenia etruskiego, które Rzymianie przejęli i zmodyfikowali około 500 roku przed naszą erą. Są to cyfry zapisywane ich skrótami literowymi. Rzymianie używali następujących znaków: I1 V- 5 X 10 L 50 C 100 D 500 M1000 Przy tworzeniu liczb stosowali następujące zasady: Cyfry jednakowe są dodawane Cyfry mniejsze stojące przed większymi są od nich odejmowane, cyfry mniejsze stojące za większymi są do nich dodawane Ponadto: Znak I może wystąpić tylko przed V i X. Znak X może wystąpić tylko przed L i C. Znak C może wystąpić tylko przed D i M.

Slide 13

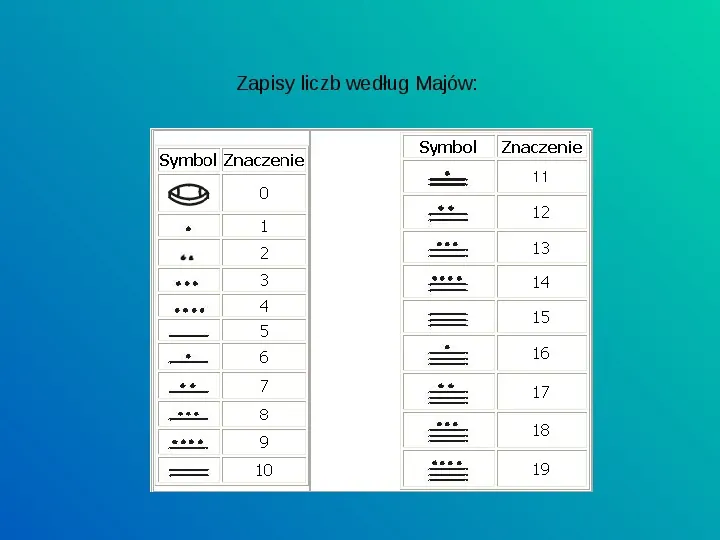
Zapisy liczbowe odnajdujemy także na kontynencie amerykańskim. Ciekawy system zapisu liczb stworzyło indiańskie plemię Majów, zamieszkujące południowo-wschodnią część Meksyku, Gwatemalę i część Hondurasu. Plemię to odkryli Hiszpanie w XVI wieku, gdy chyliło się już ku upadkowi. Już od początków naszej ery jednostki do czterech włącznie Majowie oznaczali kropkami, jednostkę nazywali kin, czyli dzień, a pięć oznaczali poziomą kreską. Zero oznaczone było rysunkiem przypominającym skorupkę ślimaka lub jak inni twierdzą półotwarte oko i zostało użyte w zapisach po raz pierwszy ok.500 r. n. e. Jest to więc najstarszy symbol zera. Zapis liczb był dokonywany nie w kierunku poziomym jak u większości narodów, lecz w kierunku pionowym, tak, że najwyższe rzędy zapisywane były u góry a jednostki na dole.

Slide 14

Zapisy liczb według Majów:

Slide 15

Dzięki stworzeniu w 1840 roku alfabetu Morsea znaki cyfr można przesyłać na odległość za pomocą impulsów elektrycznych. W alfabecie tym każdy znak zastępowany jest serią sygnałów krótkich (tzw. kropek) oraz długich (kresek). Kreska powinna trwać co najmniej tyle czasu, co trzy kropki. Odstęp pomiędzy elementami znaku powinien trwać jedną kropkę. Odstęp pomiędzy poszczególnymi znakami - jedną kreskę. Odstęp pomiędzy grupami znaków - trzy kreski. Cyfr a Kod (wersja pełna) Kod (wersja skrócona) 1 2 3 4 5 6 7 8 9 0

Slide 16

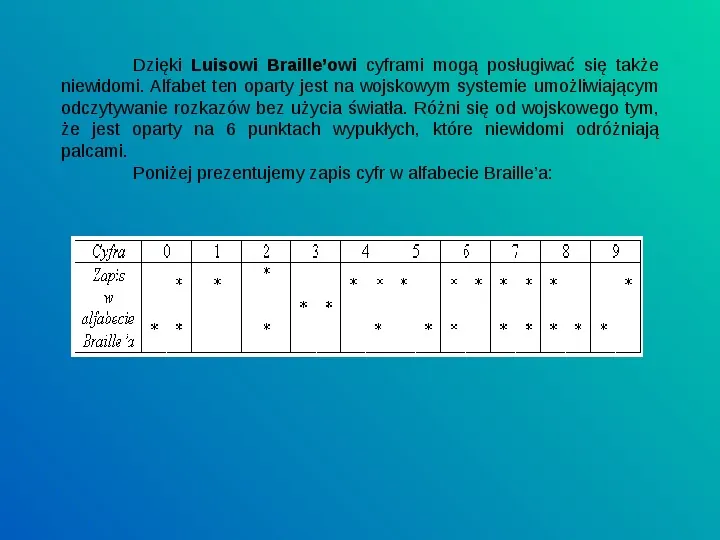
Dzięki Luisowi Brailleowi cyframi mogą posługiwać się także niewidomi. Alfabet ten oparty jest na wojskowym systemie umożliwiającym odczytywanie rozkazów bez użycia światła. Różni się od wojskowego tym, że jest oparty na 6 punktach wypukłych, które niewidomi odróżniają palcami. Poniżej prezentujemy zapis cyfr w alfabecie Braillea: