Pole równoległoboku

Zobacz slidy

Treść prezentacji

Slide 1

MATEMATYK A V JAK KLASA OBLICZYĆ POLE RÓWNOLEGŁOBOKU ?

Slide 2

Narysujmy równoległobok a D C h A B

Slide 3

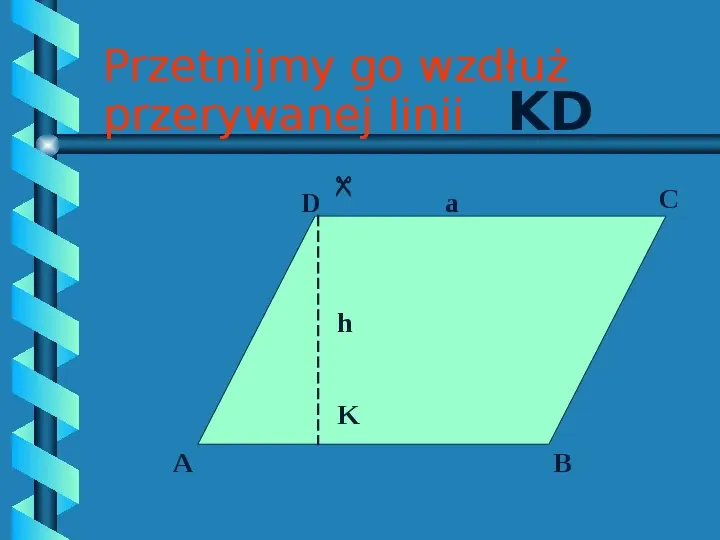
D Przetnijmy go wzdłuż przerywanej linii KD C a h K A B

Slide 4

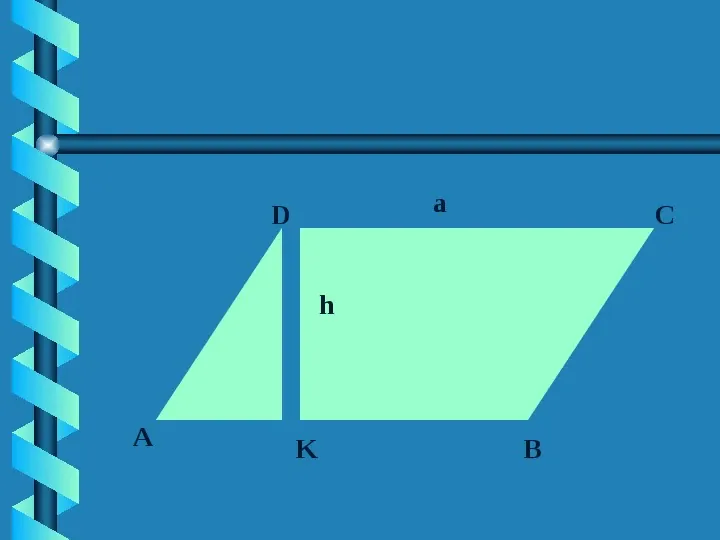
a D C h A K B

Slide 5

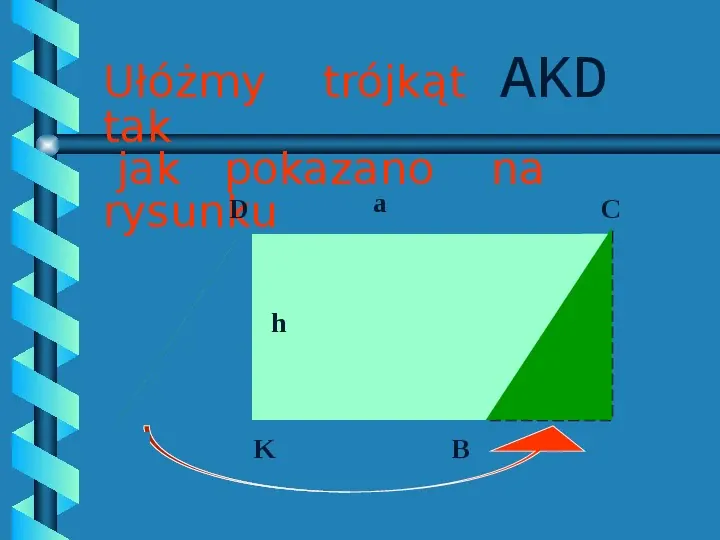
Ułóżmy trójkąt AKD tak jak pokazano na a D C rysunku h A K B

Slide 6

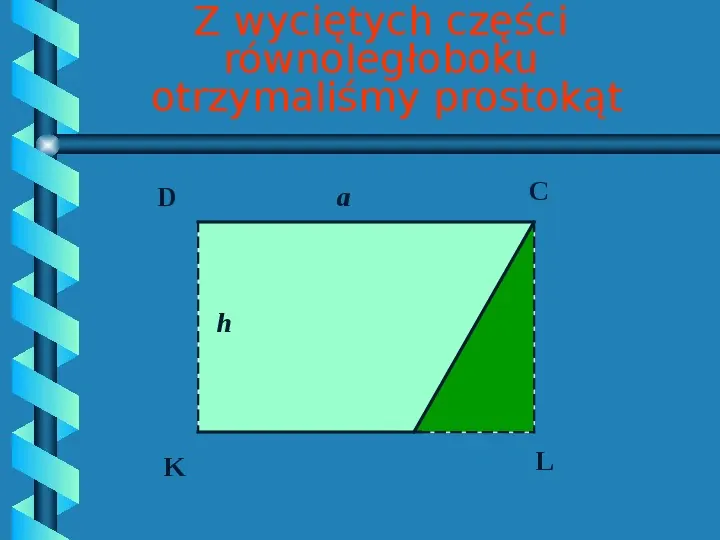
Z wyciętych części równoległoboku otrzymaliśmy prostokąt D a C h K L

Slide 7

WNIOSEK : Pole równoległoboku ABCD jest równe polu prostokąta KLCD PABCD PKLCD

Slide 8

Pole prostokąta potrafimy już obliczyć : PKLCD KL DK gdzie : D C h K a KL a ; DK h , czyli : PKLCD a h L

Slide 9

Korzystając z wniosku otrzymujemy : Pole równoległoboku jest równe iloczynowi długości jego boku i wysokości opuszczonej na ten bok.

Slide 10

Równoległobok ma dwie różne wysokości N M h1 b h K a L Zatem : PKLMN ah lub PKLMNbh1

Slide 11

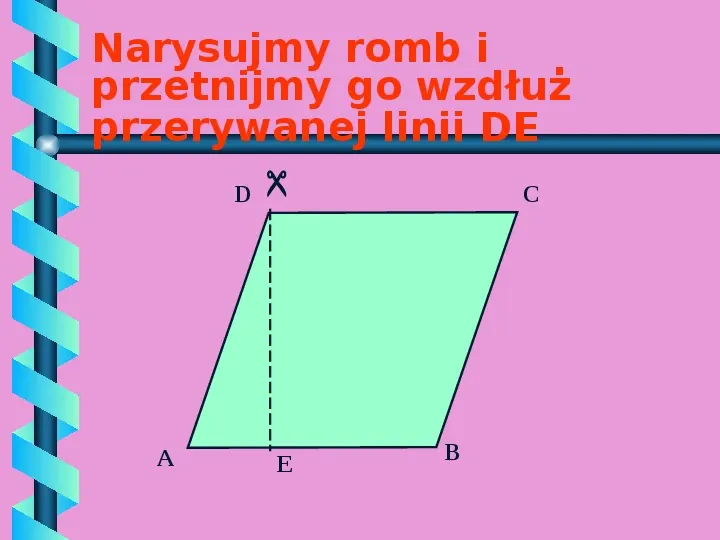
D A Narysujmy romb i przetnijmy go wzdłuż przerywanej linii DE E C B

Slide 12

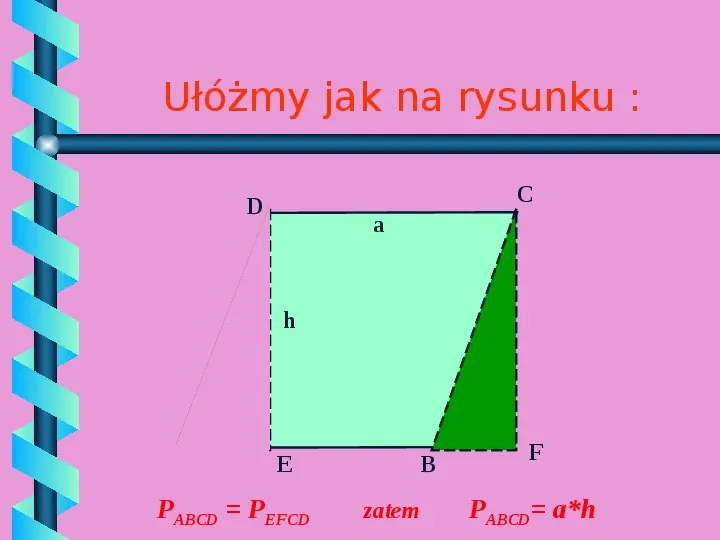
Ułóżmy jak na rysunku : C D a h A E PABCD PEFCD B zatem F PABCD ah

Slide 13

Wniosek : Pole rombu jest równe iloczynowi długości jego boku i wysokości opuszczonej na ten bok

Slide 14

Romb to również równoległobok, który ma wszystkie boki równe Zastanów się ! Jak obliczyć pole rombu ?

Slide 15

? ! Czy pole rombu, tak jak i równoległoboku można obliczyć dwoma sposobami ( wykorzystując wysokości )? NIE ! Ponieważ wysokości rombu są sobie równe

Slide 16

UWAG A !!! Istnieje jednak inny sposób obliczenia pola rombu wykorzystujący długości jego przekątnych.

Slide 17

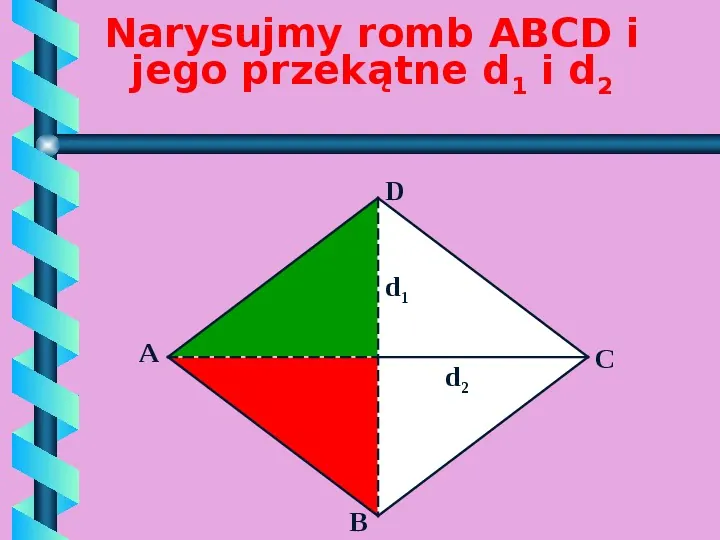
Narysujmy romb ABCD i jego przekątne d1 i d2 D d1 A d2 B C

Slide 18

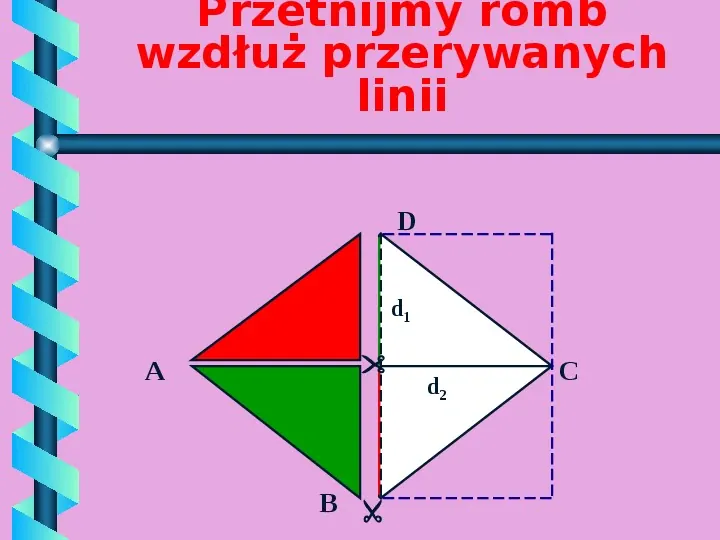
Przetnijmy romb wzdłuż przerywanych linii D d1 A B d2 C

Slide 19

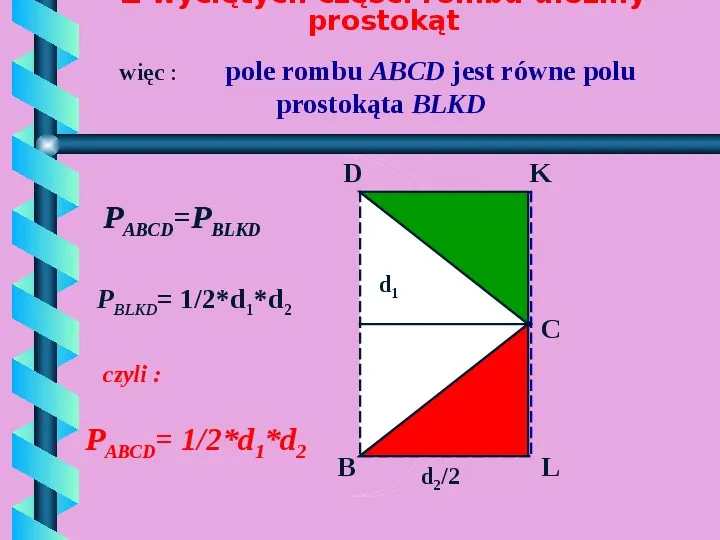
Z wyciętych części rombu ułóżmy prostokąt więc : pole rombu ABCD jest równe polu prostokąta BLKD D K PABCDPBLKD d1 PBLKD 12d1d2 C czyli : PABCD 12d1d2 B d22 L

Slide 20

Wniosek : Pole rombu jest równe połowie iloczynu długości jego przekątnych

Slide 21

Koniec Elżbieta Maciejasz