Pola figur

Zobacz slidy

Treść prezentacji

Slide 1

Prezentację opracowała mgr Renata Koperwas nauczycielka ZSP w Krasnobrodzie

Slide 2

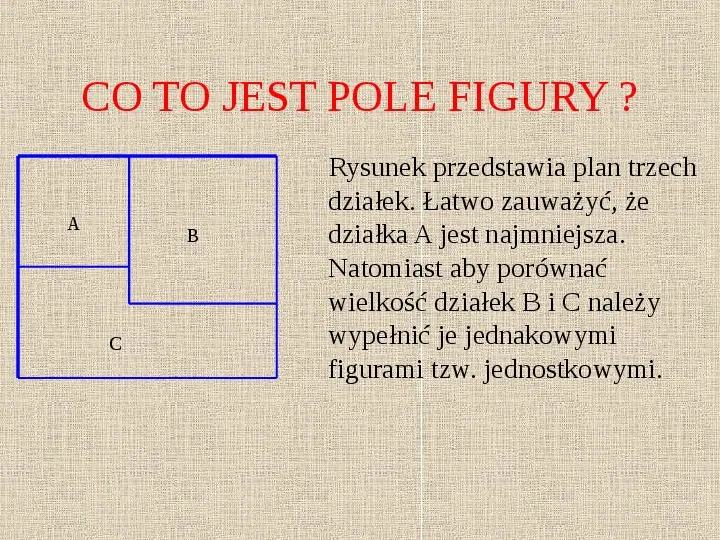
CO TO JEST POLE FIGURY ? A B C Rysunek przedstawia plan trzech działek. Łatwo zauważyć, że działka A jest najmniejsza. Natomiast aby porównać wielkość działek B i C należy wypełnić je jednakowymi figurami tzw. jednostkowymi.

Slide 3

CO TO JEST POLE FIGURY ? A B C Figura C zawiera 17 kwadratów, zatem ma większą powierzchnię niż figura B, która ma 16 kwadratów.

Slide 4

CO TO JEST POLE FIGURY ? Figura obok składa się z 10 jednakowych trójkątów, więc jej pole wyrażone za pomocą tych trójkątów wynosi 10 jednostek.

Slide 5

Powszechnie stosowanymi jednostkami pola są : milimetr kwadratowy (mm2) centymetr kwadratowy (cm2) 1cm 1cm 1cm decymetr kwadratowy (dm2) metr kwadratowy (m2) kilometr kwadratowy (km2) 2 Ogrody, place, działki rolne i większe obszary mierzymy w arach (a) i hektarach (ha). Są to gruntowe jednostki pola.

Slide 6

Zależności między jednostkami pola wynikają z zależności między jednostkami długości : 1cm 10mm 1m 100cm 1cm2 100mm2 1m2 10000cm2 1010 100100

Slide 7

1 ar to pole kwadratu o boku10m, zatem 1a 100m2 1 hektar to pole kwadratu o boku 100m, zatem 1 ha 10000m2 1 ha 100a 1cm2 100mm2 1dm2 100cm2 10000mm2 1m2100dm2 10000cm2 1000000mm2 1km2 100ha 10000a 1000000 m2

Slide 8

Prostokąt o wymiarach 3cm i 4cm dzielimy na kwadraty o boku 1cm. Mamy więc 3 rzędy po 4 kwadraty, każdy o polu 1cm2. 3412 więc P 12cm2 Pole prostokąta obliczamy mnożąc długość przez szerokość tego prostokąta.

Slide 9

b a WZÓR NA POLE PROSTOKĄTA : P a b a,b długości boków prostokąta

Slide 10

a a Ponieważ kwadrat jest prostokątem, jego pole obliczamy w ten sam sposób. Wzór na pole kwadratu : P a a gdzie a oznacza długość boku kwadratu Inna postać wzoru : P a2

Slide 11

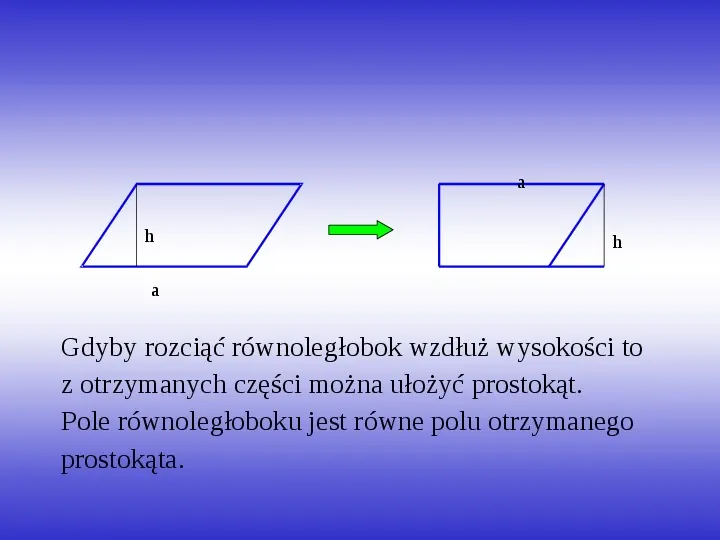
a h h a Gdyby rozciąć równoległobok wzdłuż wysokości to z otrzymanych części można ułożyć prostokąt. Pole równoległoboku jest równe polu otrzymanego prostokąta.

Slide 12

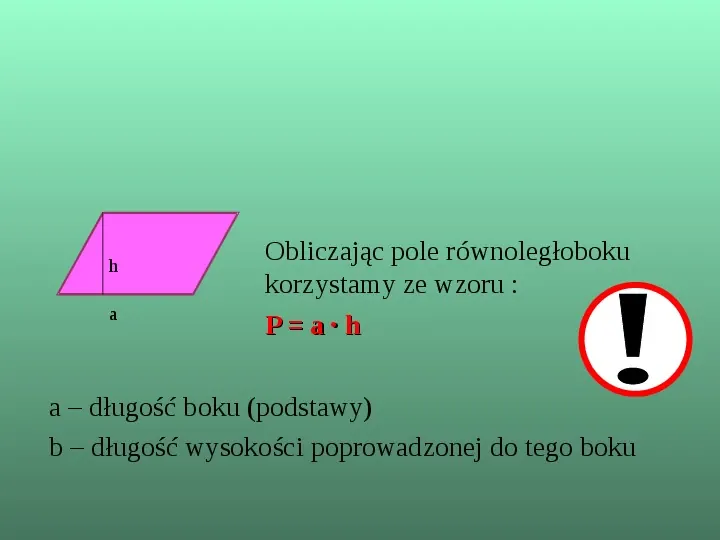
h a Obliczając pole równoległoboku korzystamy ze wzoru : P a h a długość boku (podstawy) b długość wysokości poprowadzonej do tego boku

Slide 13

Pole rombu możemy obliczyć dwoma sposobami : 1.Ponieważ romb jest równoległobokiem, więc jego pole można obliczyć tak jak pole P a h równoległoboku : h a a długość podstawy h długość wysokości poprowadzonej do tej podstawy

Slide 14

2.Dane są dwie przekątne rombu. Mając dwa jednakowe romby o przekątnych e i f, można z nich ułożyć prostokąt o bokach e i f. e e f f Prostokąt składa się z dwóch rombów, więc jego pole jest dwa razy większe niż pole każdego z tych rombów. Zatem pole rombu jest równe połowie pola prostokąta. Stąd : P ef P pole rombu e,f długości przekątnych rombu

Slide 15

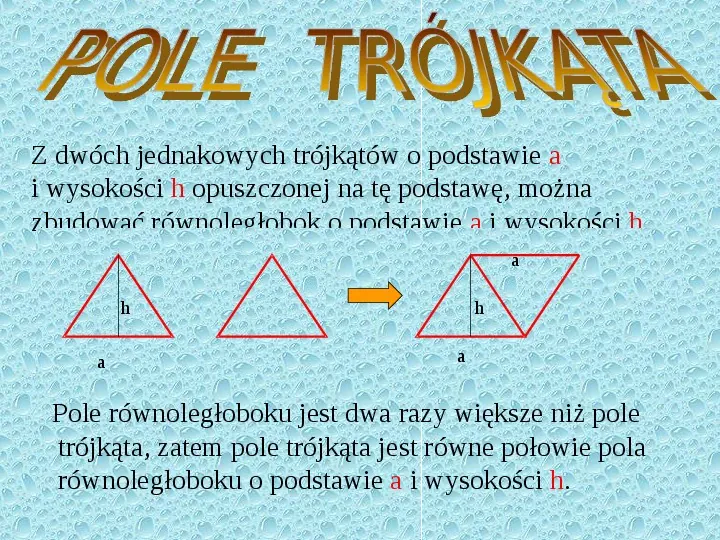
Z dwóch jednakowych trójkątów o podstawie a i wysokości h opuszczonej na tę podstawę, można zbudować równoległobok o podstawie a i wysokości h. a h a h a Pole równoległoboku jest dwa razy większe niż pole trójkąta, zatem pole trójkąta jest równe połowie pola równoległoboku o podstawie a i wysokości h.

Slide 16

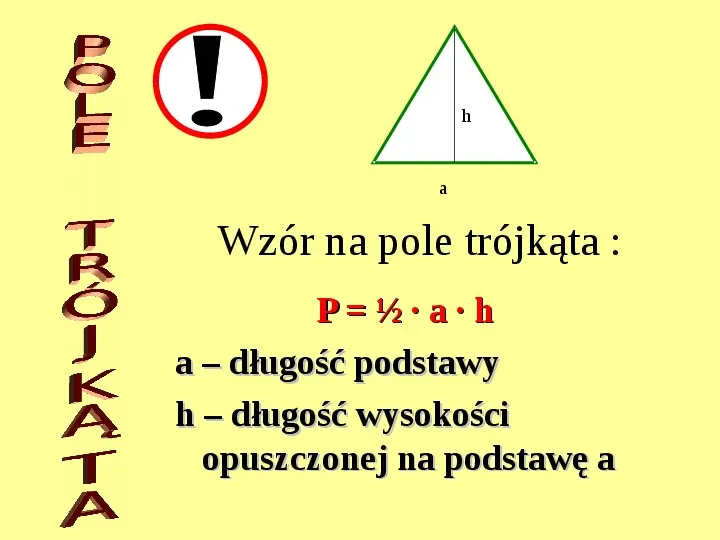
h a Wzór na pole trójkąta : P ah a długość podstawy h długość wysokości opuszczonej na podstawę a

Slide 17

b a Ponieważ wysokością dla podstawy a jest przyprostokątna b i odwrotnie, pole trójkąta prostokątnego jest równe połowie iloczynu jego przyprostokątnych. Pab a, b długości przyprostokątnych

Slide 18

Z dwóch jednakowych trapezów o podstawach długości a i b oraz wysokości h można ułożyć równoległobok o wymiarach podstawa ab i wysokość h. b h b a h a a b Równoległobok składa się z dwóch trapezów zatem jego pole jest dwa razy większe niż pole każdego z trapezów. Stąd pole trapezu jest równe połowie pola równoległoboku o wymiarach ab i h.

Slide 19

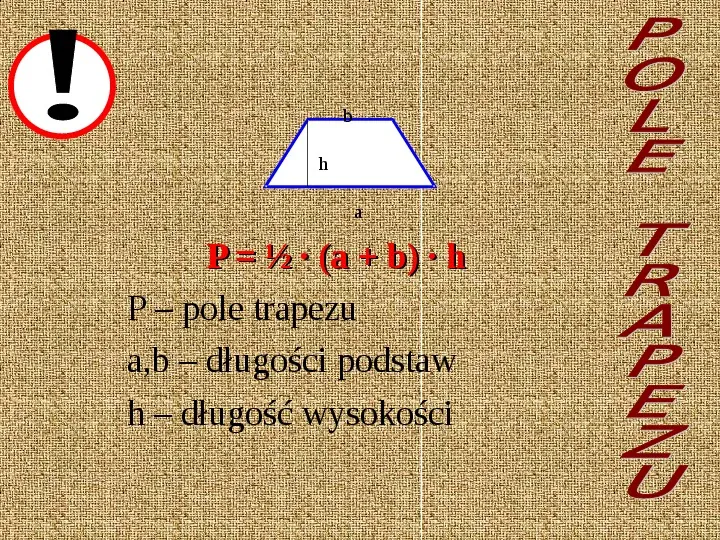
b h a P (a b) h P pole trapezu a,b długości podstaw h długość wysokości

Slide 20

e D A C S f B Przekątne deltoidu to odcinki ACe i BDf. Deltoid można podzielić na dwa trójkąty :ACD i ACB. Zatem pole deltoidu będzie sumą pól tych trójkątów. PACD e DS PACB e SB PABCD e DS eSB e (DS SB) e f Pole deltoidu jest równe połowie iloczynu długości jego przekątnych.

Slide 21

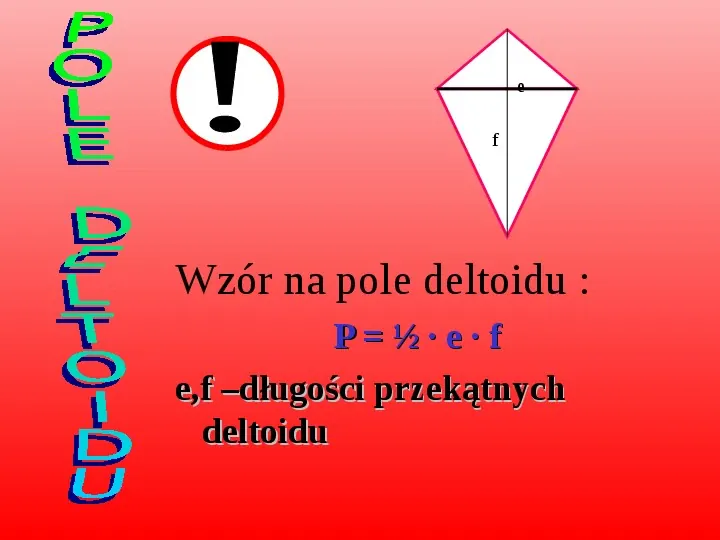
e f Wzór na pole deltoidu : P ef e,f długości przekątnych deltoidu

Slide 22

Pole figury, do której nie da się zastosować żadnego z podanych wzorów można obliczyć na dwa sposoby : 1.Dzielimy figurę na mniejsze części. Pole czworokąta będzie równe sumie pól trapezu i trójkąta.

Slide 23

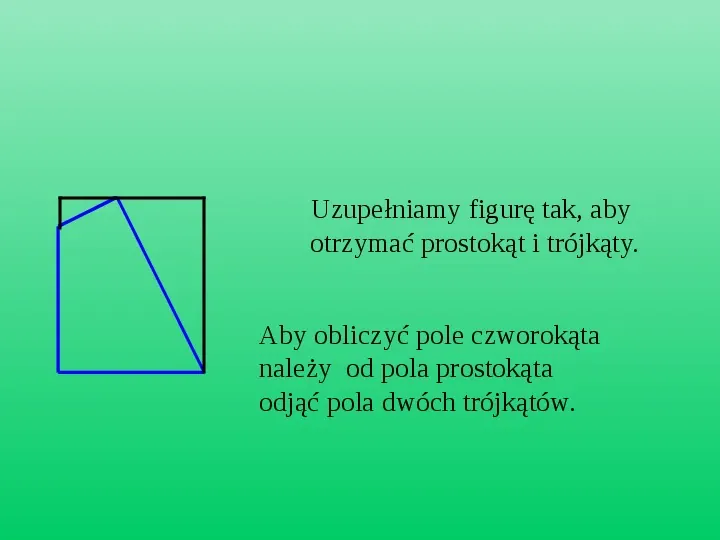
Uzupełniamy figurę tak, aby otrzymać prostokąt i trójkąty. Aby obliczyć pole czworokąta należy od pola prostokąta odjąć pola dwóch trójkątów.

Slide 24

Pola wielokątów - podsumowanie Pole prostokąta : P a b Pole kwadratu : P a2 Pole równoległoboku : P a h Pole rombu : P a h lub P e f Pole trójkąta : P a h Pole trapezu : P (ab) h Korzystając z tych wzorów można obliczać pola innych wielokątów. UWAGA przy obliczaniu pól figur należy pamiętać, aby wszystkie potrzebne wymiary podane były w tych samych jednostkach.

Slide 25

Powyższa prezentacja opracowana została na podstawie podręcznika Matematyka 5 Gdańskiego Wydawnictwa Oświatowego. Dany fragment prezentacji może być wprowadzeniem do nowej lekcji w kl.IV lubV, albo przypomnieniem wiadomości w kl.VI. Znak ten zwraca uwagę na pojawiający się wzór na obliczanie pola danej figury.