Schemat blokowy algorytmu

Zobacz slidy

Treść prezentacji

Slide 2

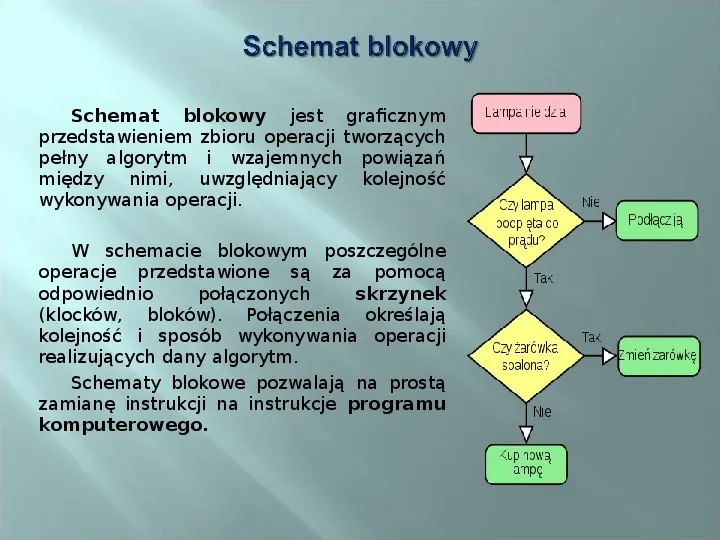
Schemat blokowy jest graficznym przedstawieniem zbioru operacji tworzących pełny algorytm i wzajemnych powiązań między nimi, uwzględniający kolejność wykonywania operacji. W schemacie blokowym poszczególne operacje przedstawione są za pomocą odpowiednio połączonych skrzynek (klocków, bloków). Połączenia określają kolejność i sposób wykonywania operacji realizujących dany algorytm. Schematy blokowe pozwalają na prostą zamianę instrukcji na instrukcje programu komputerowego.

Slide 3

strzałka - wskazuje jednoznacznie powiązania i ich kierunek operand - prostokąt, do którego wpisywane są wszystkie operacje z wyjątkiem instrukcji wyboru predykat - romb, do którego wpisywane są wyłącznie instrukcje wyboru etykieta - owal służący do oznaczania początku bądź końca sekwencji schematu (kończą, zaczynają lub przerywająprzenoszą schemat) Schemat blokowy pozwala dostrzec istotne etapy algorytmu i logiczne zależności między nimi.

Slide 4

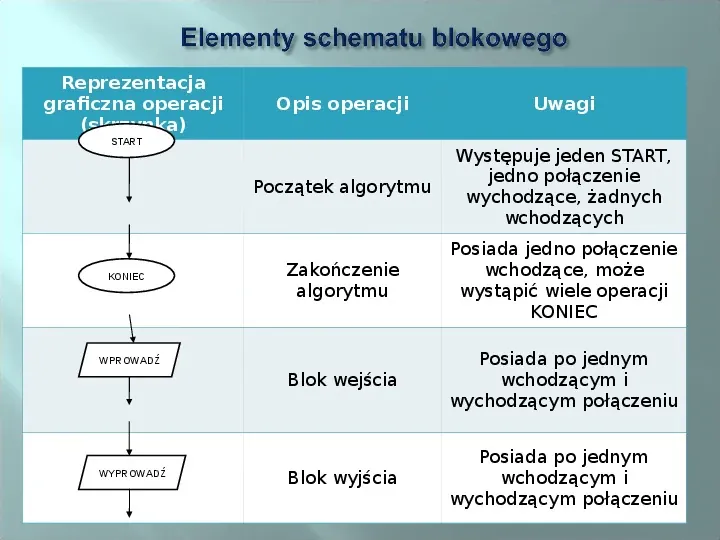
Reprezentacja graficzna operacji (skrzynka) Opis operacji Uwagi Początek algorytmu Występuje jeden START, jedno połączenie wychodzące, żadnych wchodzących Zakończenie algorytmu Posiada jedno połączenie wchodzące, może wystąpić wiele operacji KONIEC Blok wejścia Posiada po jednym wchodzącym i wychodzącym połączeniu Blok wyjścia Posiada po jednym wchodzącym i wychodzącym połączeniu START KONIEC WPROWADŹ WYPROWADŹ

Slide 5

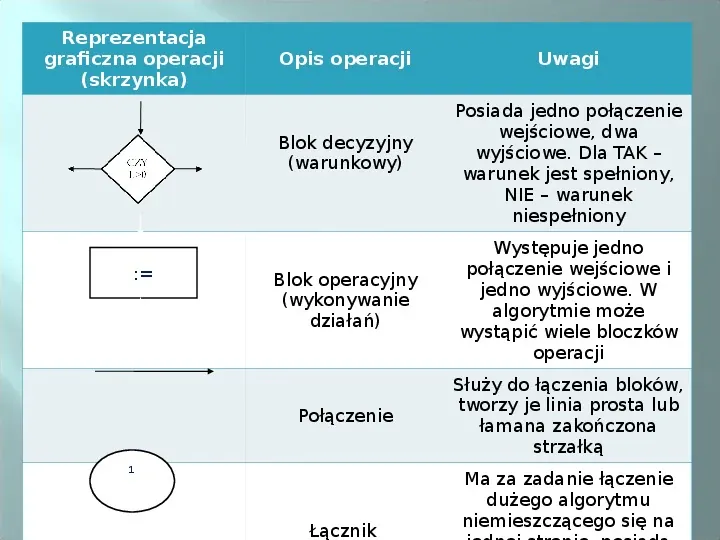
Reprezentacja graficzna operacji (skrzynka) Opis operacji Blok decyzyjny (warunkowy) : Uwagi Posiada jedno połączenie wejściowe, dwa wyjściowe. Dla TAK warunek jest spełniony, NIE warunek niespełniony Blok operacyjny (wykonywanie działań) Występuje jedno połączenie wejściowe i jedno wyjściowe. W algorytmie może wystąpić wiele bloczków operacji Połączenie Służy do łączenia bloków, tworzy je linia prosta lub łamana zakończona strzałką 1 Łącznik Ma za zadanie łączenie dużego algorytmu niemieszczącego się na

Slide 6

każda operacja, relacja lub informacja jest umieszczana w skrzynce kolejność wykonywania operacji wyznaczają połączenia między skrzynkami każde połączenie jest zaczepione początkiem do skrzynki, a końcem do innej skrzynki lub innego połączenia, żadne połączenie nie rozdziela się rozgałęzienie sieci działań możliwe jest tylko dzięki skrzynkom warunkowym schemat posiada jedną skrzynkę START i co najmniej jedną skrzynkę STOP ze skrzynki START można przejść do skrzynki STOP poruszając się po sieci działań ze skrzynki START można dotrzeć wzdłuż połączeń do dowolnej innej skrzynki schematu z każdej skrzynki istnieje przejście wzdłuż połączeń do jednej ze skrzynek STOP

Slide 7

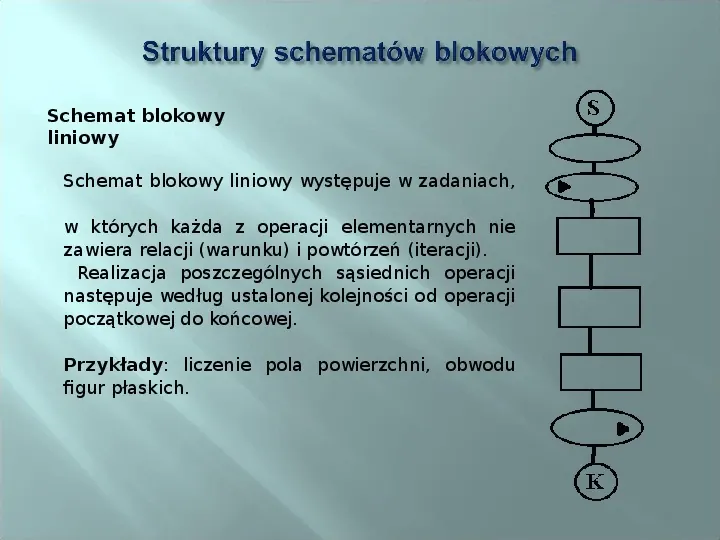
Schemat blokowy liniowy Schemat blokowy liniowy występuje w zadaniach, w których każda z operacji elementarnych nie zawiera relacji (warunku) i powtórzeń (iteracji). Realizacja poszczególnych sąsiednich operacji następuje według ustalonej kolejności od operacji początkowej do końcowej. Przykłady: liczenie pola powierzchni, obwodu figur płaskich.

Slide 8

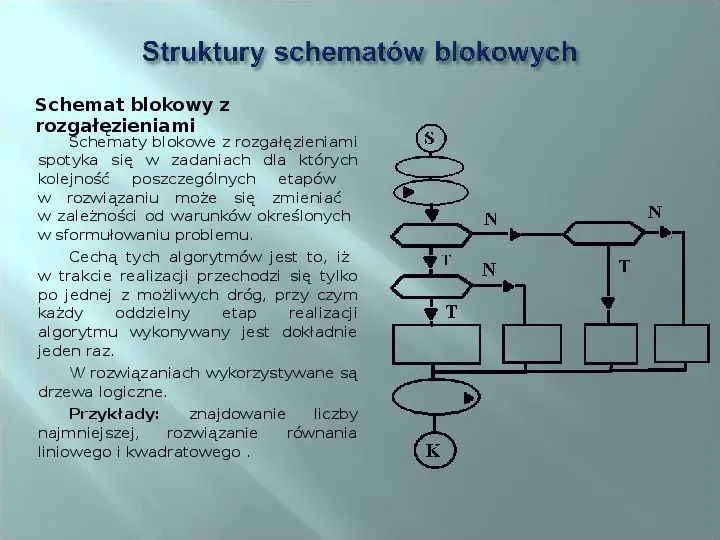
Schemat blokowy z rozgałęzieniami Schematy blokowe z rozgałęzieniami spotyka się w zadaniach dla których kolejność poszczególnych etapów w rozwiązaniu może się zmieniać w zależności od warunków określonych w sformułowaniu problemu. Cechą tych algorytmów jest to, iż w trakcie realizacji przechodzi się tylko po jednej z możliwych dróg, przy czym każdy oddzielny etap realizacji algorytmu wykonywany jest dokładnie jeden raz. W rozwiązaniach wykorzystywane są drzewa logiczne. Przykłady: znajdowanie liczby najmniejszej, rozwiązanie równania liniowego i kwadratowego .

Slide 9

Schemat blokowy cykliczny - z pętlą Algorytmy dla problemów wymagających powtarzania poszczególnych etapów procesu obliczeniowego nazywamy cyklicznymi (czyli z pętlą). Przez pętlę w schemacie blokowym rozumiemy tą część schematu, która opisuje drogę (obwód) zamkniętą zgodnie z kierunkiem połączenia (obiegu). Pętla stanowi graficzny opis powtarzania czynności. Ciąg wszystkich czynności wykonywanych przy jednokrotnym przebiegu pętli nazywamy cyklem pętli. W każdej pętli musi wystąpić: co najmniej jedna skrzynka operacyjna (np. wyliczeniowa) zawierająca opis powtarzanej czynności modyfikacja w każdym cyklu co najmniej jednej wartości zmiennej występującej w pętli skrzynka decyzyjna z warunkiem, czy pętla ma być nadal powtarzana czy też zakończona Często w pętli występują zmienne nazywane licznikami, których wartości w algorytmie określają ilość zrealizowanych cykli pętli.

Slide 10

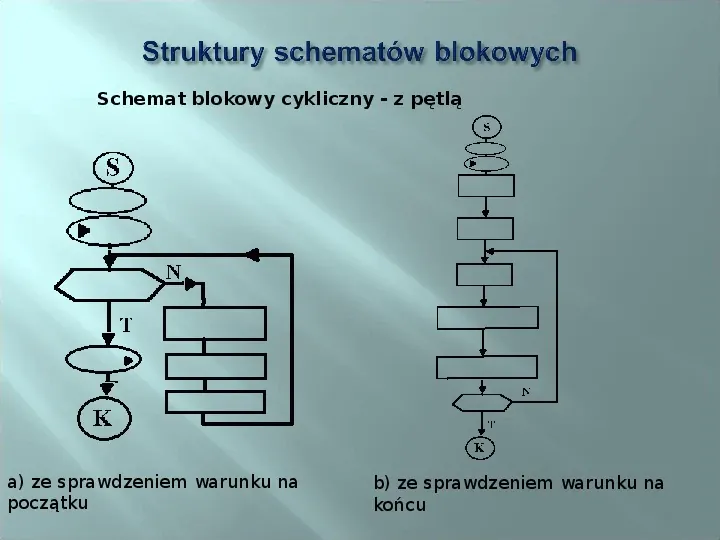
Schemat blokowy cykliczny - z pętlą a) ze sprawdzeniem warunku na początku b) ze sprawdzeniem warunku na końcu

Slide 11

Algorytm, który został poprawnie skonstruowany posiada następujące cechy: posiada dane wejściowe niekoniecznie w formie numerycznej pochodzące z dobrze zdefiniowanego źródła produkuje pewien wynik niekoniecznie numeryczny jest precyzyjnie zdefiniowany, tzn. każdy krok algorytmu musi być jednoznacznie określony jest skończony każdy algorytm musi dać wynik, rozwiązanie

Slide 12

Działa według jednego z dwóch przedstawionych schematów: jeśli spełniony jest warunek W, wykonaj instrukcję A jeśli spełniony jest warunek W, to wykonaj instrukcję A; w przeciwnym razie wykonaj instrukcję B Instrukcje A i B opisują pojedynczą instrukcję lub instrukcję składającą się z ciągu instrukcji wykonywanych sekwencyjnie. Instrukcja warunkowa pozwala dokonać wyboru jednej z dwóch dalszych dróg wykonania algorytmu. Lista kroków instrukcja warunkowa przykład: K01: Podnieś słuchawkę K02: Wybierz cyfrę 1 K03: Wybierz cyfrę 1 K04: Wybierz cyfrę 2 K05: Czy połączyłeś się z telefonem alarmowym? A.Jeśli TAK, to przejdź do K06 B.Jeśli NIE, to przejdź do K07 K06: Wezwij pomoc K07: Odłóż słuchawkę

Slide 13

Wielokrotne powtarzanie niektórych instrukcji jest cechą charakterystyczną wielu algorytmów, nie zawsze jednak możemy określić dokładnie liczbę powtórzeń. Liczba powtórzeń może zależeć od spełnienia pewnych warunków. Wielokrotne powtarzanie instrukcji umożliwiają instrukcje iteracyjne (pętle). Działają one według następującego schematu: wykonuj instrukcję A dokładnie n razy Iteracja to technika algorytmiczna polegająca na wykonaniu tej samej instrukcji dla n zmiennych. Lista kroków pętla przykład: K01: Podnieś słuchawkę K02: Wykonaj czynność dwa razy A. Wybierz cyfrę 1 K03: Wybierz cyfrę 2 K04: czy połączyłeś się z telefonem alarmowym? A.Jeśli TAK, to przejdź do K05 B.Jeśli NIE, to przejdź do K06 K05: Wezwij pomoc K06: Odłóż słuchawkę

Slide 14

Powtarzamy wybieranie numeru aż do uzyskania połączenia. Dopiszemy w tym celu polecenie będące drugim rodzajem instrukcji iteracyjnej: powtarzaj wykonywanie instrukcji A aż do spełnienia warunku W Czym jest instrukcja A, czym warunek W ? Instrukcja A - podniesienie słuchawki, wybranie numeru Warunek W - uzyskanie połączenia z wybranym numerem Lista kroków pętla przykład: K01: Czy słuchawka jest odłożona? A.Jeśli TAK, to przejdź K02 B.Jeśli NIE, to odłóż słuchawkę K02: Podnieś słuchawkę K03: Wykonaj czynność dwa razy A. Wybierz cyfrę 1 K04: Wybierz cyfrę 2 K05: czy połączyłeś się z telefonem alarmowym? A.Jeśli TAK, to przejdź do K06 B.Jeśli NIE, to przejdź do K07 K06: Wezwij pomoc K07: Odłóż słuchawkę

Slide 15

Jeżeli nadal słychać w słuchawce sygnał zajętości linii, czynność należałoby powtórzyć. Wykonujemy te czynności dopóki linia nie będzie wolna. W takim przypadku stosujemy instrukcję, która działa według schematu: dopóki warunek W jest spełniony, wykonuj instrukcję A Lista kroków pętla przykład: K01: Czy słuchawka jest odłożona? A. Jeśli TAK, to przejdź K02 B. Jeśli NIE, to odłóż słuchawkę K02: Podnieś słuchawkę K03: Czy linia jest zajęta ? A. Jeśli TAK, to: a. Odłóż słuchawkę b. Podnieś słuchawkę c. Przejdź do kroku K03 B. Jeśli NIE, to przejdź do K04 K04: Wykonaj czynność dwa razy A. Wybierz cyfrę 1 K05: Wybierz cyfrę 2 K06: czy połączyłeś się z telefonem alarmowym? A. Jeśli TAK, to przejdź do K06 B. Jeśli NIE, to przejdź do K07 K07: Wezwij pomoc K08: Odłóż słuchawkę

Slide 16

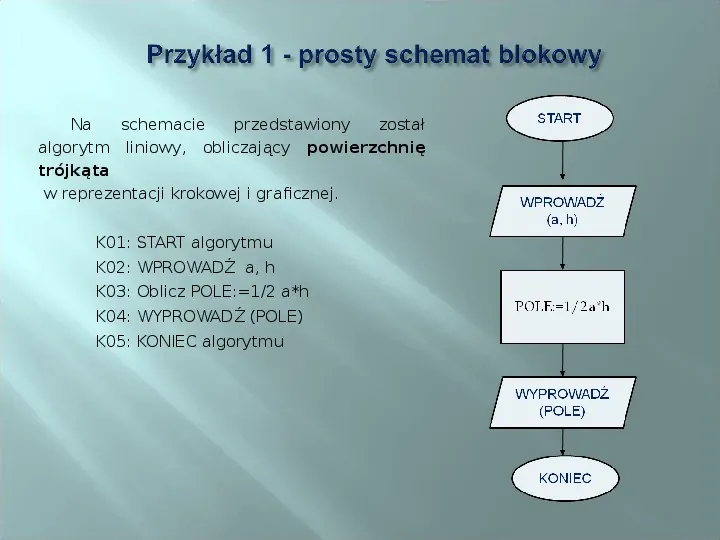
Na schemacie przedstawiony został algorytm liniowy, obliczający powierzchnię trójkąta w reprezentacji krokowej i graficznej. K01: START algorytmu K02: WPROWADŹ a, h K03: Oblicz POLE:12 ah K04: WYPROWADŹ (POLE) K05: KONIEC algorytmu

Slide 17

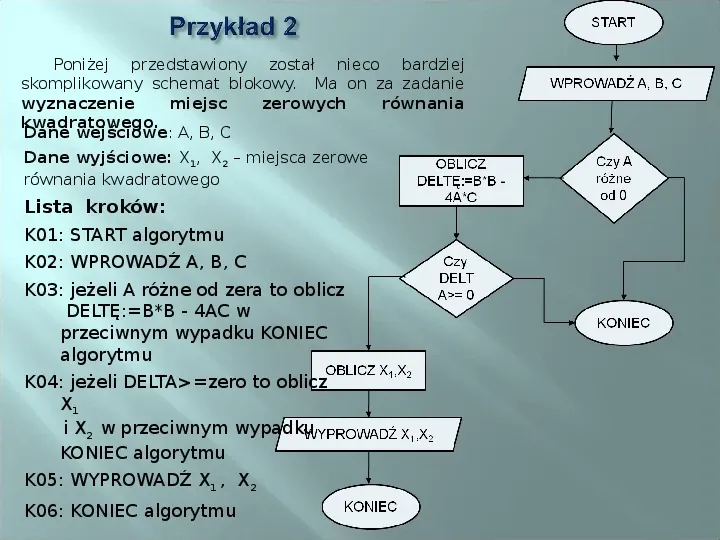
Poniżej przedstawiony został nieco bardziej skomplikowany schemat blokowy. Ma on za zadanie wyznaczenie miejsc zerowych równania kwadratowego. Dane wejściowe: A, B, C Dane wyjściowe: X1, X2 miejsca zerowe równania kwadratowego Lista kroków: K01: START algorytmu K02: WPROWADŹ A, B, C K03: jeżeli A różne od zera to oblicz DELTĘ:BB - 4AC w przeciwnym wypadku KONIEC algorytmu K04: jeżeli DELTAzero to oblicz X1 i X2 w przeciwnym wypadku KONIEC algorytmu K05: WYPROWADŹ X1 , X2 K06: KONIEC algorytmu

Slide 18

Przykład pokazuje w jaki sposób znaleźć minimum spośród dwóch liczb całkowitych a i b. Program wyprowadza wartość wyniku, w przypadku gdy liczby są sobie równe wyprowadza odpowiedni komunikat. Dane wejściowe: a, b liczby całkowite Dane wyjściowe: min - minimalna wartość a lub b Lista kroków K01: Wprowadź dwie liczby całkowite a i b: wykonuj K02 K02: Jeśli ab, to podstaw mina, wyprowadź wynik mina. Przejdź do K05: w przeciwnym przypadku przejdź do K03 K03: Sprawdź czy ba, jeśli TAK to podstaw minb: wyprowadź wynik minb. Przejdź do K05: w przeciwnym przypadku przejdź do K04 K04: Podstaw mina, wyprowadź wynik minab. Przejdź do K05 K05: Koniec

Slide 19

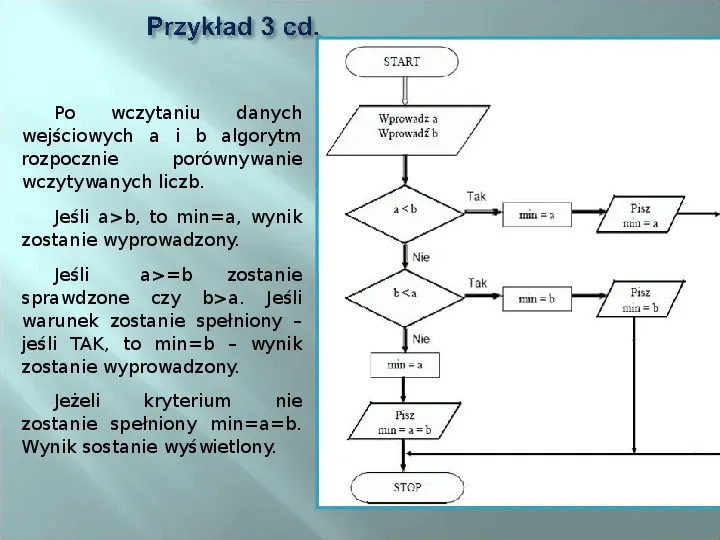
Po wczytaniu danych wejściowych a i b algorytm rozpocznie porównywanie wczytywanych liczb. Jeśli ab, to mina, wynik zostanie wyprowadzony. Jeśli ab zostanie sprawdzone czy ba. Jeśli warunek zostanie spełniony jeśli TAK, to minb wynik zostanie wyprowadzony. Jeżeli kryterium nie zostanie spełniony minab. Wynik sostanie wyświetlony.

Slide 20

Cormen T.H., Leiserson Ch.E., Rivest R.L., Stein C.: Wprowadzenie do algorytmow. WNT, Warszawa, 2005 Wroblewski P.: Algorytmy, struktury danych i techniki programowania, Wydanie III, Helion, Gliwice, 2003 Donald E. Knuth: Sztuka programowania. T. 1. Warszawa: Wydawnictwo Naukowo-Techniczne, 2002 N. Wirth: Algorytmy struktury danych programy. WNT, Warszawa, 2004. pl.wikipedia.org algorytm.org neuralnets.eu encyklopedia.pwn.pl