Od cyfr egipskich do cyfr arabskich

Zobacz slidy

Treść prezentacji

Slide 3

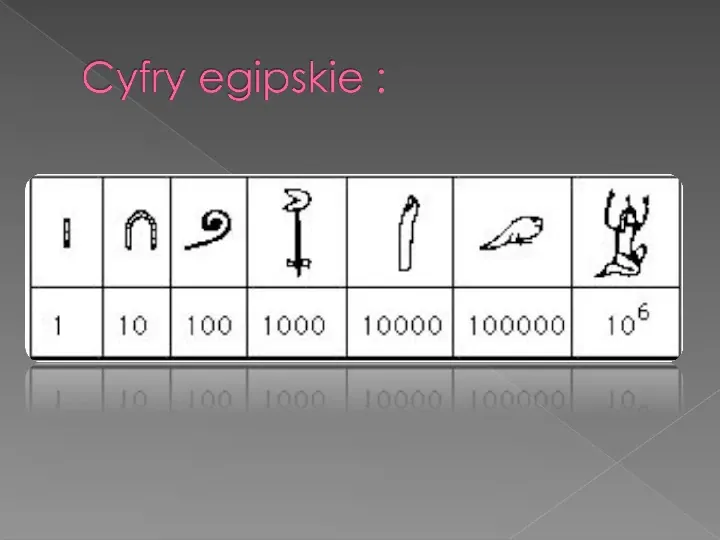
Egipcjanie nie znali zera. Starożytne cyfry egipskie były używane w Egipcie, aż do wczesnych lat pierwszego tysiąclecia naszej ery. Był to system dziesiętny, często zaokrąglany w górę, zapisywany przy użyciu hieroglifów. System zapisu przez hieratykę wymuszał skończony zapis liczb.

Slide 4

Zapisując liczbę za pomocą tych znaków , powtarzano je odpowiednią ilość razy. Ponieważ nie był to system pozycyjny, nie było ważne, w którym miejscu hieroglify są narysowane. Dodawanie w tym systemie polegało na liczeniu poszczególnych znaków. Pełne dziesiątki jednakowych znaków zastępowało się znakiem wyższego rzędu.

Slide 6

Babilończycy jako pierwsi stosowali pozycyjny system liczenia. Babilońskich znaków używano w Mezopotamii około 5000 lat temu, zachowały się do naszych czasów na glinianych tabliczkach. System babiloński może wydawać się skomplikowany, jednak w rzeczywistości Babilończycy potrzebowali tylko dwóch symboli - dla oznaczenia jedności i dziesiątek.

Slide 7

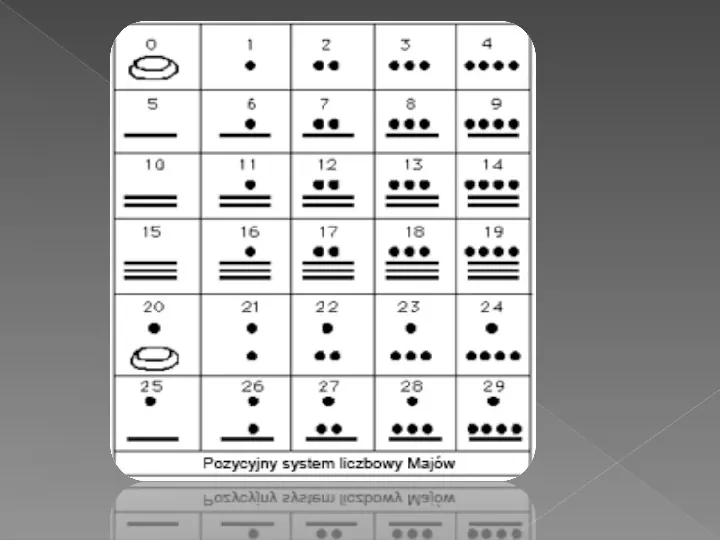
Bardzo oryginalny system zapisywania liczb stworzyło indiańskie plemię Majów. Jako jedni z pierwszych wynaleźli zero (ok. 500 r. p.n.e. a więc później niż Sumerowie, lecz wcześniej od Hindusów). Zero zaznaczane było rysunkiem przypominającym skorupkę ślimaka lub - jak inni twierdzą - półotwarte oko. Liczby zapisywano w postaci kombinacji kropek i kresek. Odpowiednio pogrupowane stanowiły (wraz z zerem) podstawowy zestaw ,,cyfr od 0 do 19. Liczbę w tym systemie podaję się mnożąc cyfry przez kolejne potęgi 20 ,a następnie wyznacza się iloczyny częściowe .Cyfry Majowie pisali od góry do dołu .

Slide 9

Do programowania używa się systemu dwójkowego. Podstawą tego systemu jest liczba 2 , a do zapisu liczb w systemie dwójkowym używa się cyfr 0,1. Kolejne rzędy w liczbie liczymy od prawej do lewej i są one kolejnymi potęgami liczby 2 . Wartość liczby jest sumą iloczynów cyfr 0 i 1 przez potęgi liczby 2. Np. (1001011101)21290280271260 2512412312202112051264 16841599

Slide 10

Cyfry arabskie, właściwie cyfry indyjskie europeizowane cyfry stosowane obecnie powszechnie na całym świecie do zapisywania liczb. Są to kolejno znaki: 0, 1, 2, 3, 4, 5, 6, 7, 8 oraz 9 i pierwotnie służyły do zapisu liczb w systemie dziesiętnym.

Slide 11

Odp. a)24 b)100 c)385 d)160

Slide 12

a) b) c) (11011101)2 (11111111)2 (1100110011)2 Odp. a)221 b)255 c)819

Slide 14

Źródła : Wikipedia Podręcznik