Bryły obrotowe

Zobacz slidy

Treść prezentacji

Slide 1

PREZENTACJA BRYŁY OBROTOWE WALEC STOŻEK KULA WYKONAŁA: mgr Katarzyna Kostrowska

Slide 2

WALEC C D Odcinek BD nazywamy tworzącą- l Odcinek AB jest promieniem podstawy- r Koło o środku A jest podstawą dolną Koło o środku C jest podstawą górną Odcinek AC jest wysokością walca- h A B

Slide 3

WALEC-WZORY Pole powierzchni całkowitej: Pc 2πr(rh) Pole powierzchni bocznej: Pb 2πrh Objętość walca: V πr2h

Slide 4

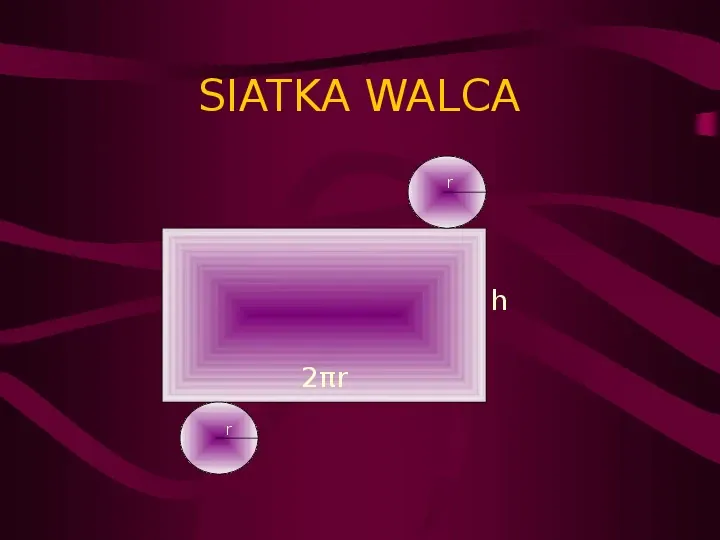
SIATKA WALCA r h 2πr r

Slide 5

PRZEKRÓJ OSIOWY WALCA Przekrojem osiowym walca jest prostokąt o wymiarach 2r i h h 2r

Slide 6

PRZEKRÓJ POPRZECZNY WALCA r r Przekrojem poprzecznym walca jest koło o promieniu r

Slide 7

ZADANIE 1-WALEC Oblicz pole boczne i pole całkowite walca powstałego przez obrót prostokąta o bokach 3cm i 5cm wokół dłuższego boku. Pb 2πrh Pc 2πr(rh) Pb 2π35 Pc Pb 2π15 Pc 2π3(35) 2π(915) 5 Pb 30π cm2 cm2 Pc 48π 3 Odp: Pole boczne walca wynosi 30π cm2, natomiast pole całkowite wynosi 48π cm2.

Slide 8

ZADANIE 2-WALEC Oblicz objętość puszki w kształcie walca o długości średnicy 5cm i wysokości 10cm. Obliczam objętość puszki: V πr2h V π(2.5)210 V π6.2510 V 62.5π cm3 Odp: Objętość puszki wynosi 62.5π cm3. Obliczam promień: r 5 2.5cm h 10cm

Slide 9

STOŻEK C A B Powstaje przez obrót trójkąta prostokątnego ABC wokół przyprostokątnej Odcinek CB nazywamy tworzącą l Odcinek AB jest promieniem podstawy r Koło o środku A jest podstawą Odcinek AC jest wysokością stożka - h

Slide 10

STOŻEK-WZORY Pole powierzchni całkowitej: Pc πr(lr) Pole powierzchni bocznej: Pb πrl Objętość stożka: V 1πr2h

Slide 11

SIATKA STOŻKA Siatka stożka składa się z wycinka koła o promieniu l, oraz koła o promieniu r. l 2πr r

Slide 12

PRZEKRÓJ OSIOWY STOŻKA l l r Przekrojem osiowym stożka jest trójkąt równoramienny.

Slide 13

PRZEKRÓJ POPRZECZNY STOŻKA Przekrojem poprzecznym stożka jest koło lub punkt. r

Slide 14

ZADANIE 1-STOŻEK Tworząca stożka ma długość 6 cm i jest nachylona do płaszczyzny podstawy stożka pod kątem 60. Oblicz pole powierzchni całkowitej stożka. l 6 cm r 3 cm r 60 Pc πr(lr) Pc π3(63) Pc π39 Pc 27π cm2 Odp: Pole powierzchni całkowitej stożka wynosi 27π cm2.

Slide 15

ZADANIE 2-STOŻEK Oblicz pole całkowite i objętość figury powstałej w wyniku obrotu trójkąta równobocznego wokół dowolnego boku o wymiarze 6cm. V 1 πr2h Pc πr(lr) V 1(326) Pc π3(63) V π(96) V 18π cm3 Pc π(189) Pc 27π cm2 l 6cm r 3cm Odp: Objętość stożka wynosi 18π cm 3, natomiast pole całkowite 27π cm 2.

Slide 16

KULA Przekrojem kuli jest koło

Slide 17

KULA-WZORY Pole powierzchni: Pp 4πr2 Objętość kuli: V4πr3

Slide 18

PRZEKRÓJ OSIOWY KULI Przekrój osiowy kuli nazywamy kołem wielkim

Slide 19

ZADANIE 1-KULA Oblicz objętość kuli wiedząc, że średnica wynosi 18cm. Obliczam r: r 18 9cm V V V V Odp: Objętość kuli wynosi 243π cm3. πr3 4π93 4π729 243π cm3 4

Slide 20

ZADANIE 2-KULA Oblicz pole powierzchni kuli mając dany promień równy 3cm. Pp 4πr2 Pp 4π32 Pp 4π9 Pp 36π cm2 Odp: Pole powierzchni kuli wynosi 36π cm2.