Bryły

Zobacz slidy

Treść prezentacji

Slide 1

Bry Graniastosłupyły Ostrosłupy Bryły obrotowe Dalej

Slide 2

Graniastos łupy Graniastosłup to wielościan, którego dwie ściany (zwane podstawami) są przystającymi wielokątami leżącymi w płaszczyznach równoległych, a pozostałe ściany są równoległobokami. Rodzaje graniastosłupów : Graniastosłup prosty - graniastosłup w którym krawędzie boczne są prostopadłe do podstaw.   Graniastosłup pochyły - graniastosłup w którym krawędzie boczne nie są prostopadłe do podstawy, długość wysokości jest krótsza od długości krawędzi bocznej.   Prostopadłościan - graniastosłup w którym wszystkie ściany są prostokątami   Graniastosłup prawidłowy - graniastosłup prosty, którego podstawa jest wielokąt foremny. Równoległościan to graniastosłup, którego wszystkie ściany są Powrótrównoległobokami. Dalej

Slide 3

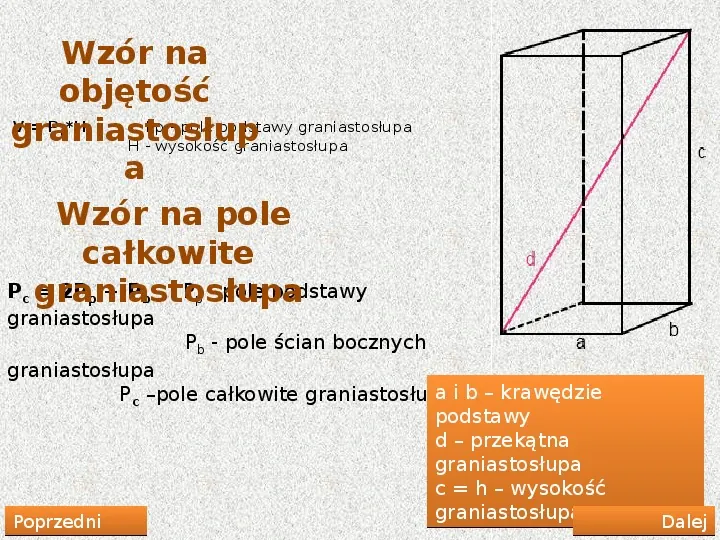
Wzór na objętość  V P H           Pp - pole podstawy graniastosłupa graniastosłup                       H - wysokość graniastosłupa a  Wzór na pole całkowite P graniastosłupa 2P P P - pole podstawy p c p b       p graniastosłupa                            Pb - pole ścian bocznych graniastosłupa a i b krawędzie Pc pole całkowite graniastosłupa podstawy d przekątna graniastosłupa c h wysokość graniastosłupa Poprzedni Dalej

Slide 4

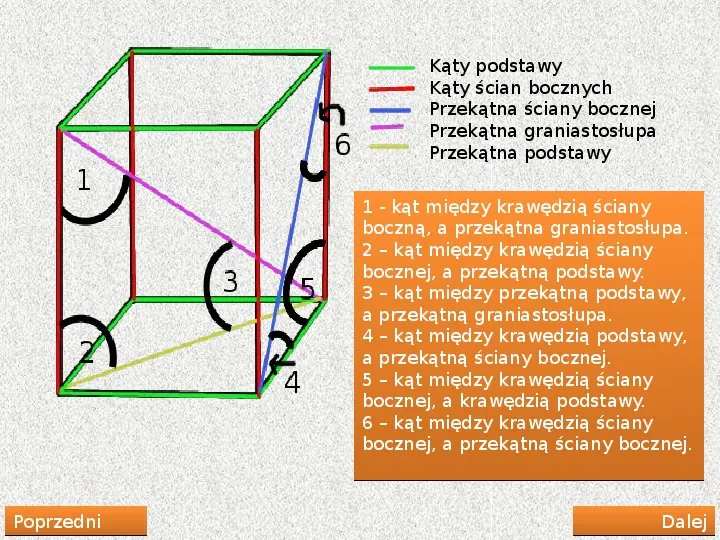
Kąty podstawy Kąty ścian bocznych Przekątna ściany bocznej Przekątna graniastosłupa Przekątna podstawy 1 - kąt między krawędzią ściany boczną, a przekątna graniastosłupa. 2 kąt między krawędzią ściany bocznej, a przekątną podstawy. 3 kąt między przekątną podstawy, a przekątną graniastosłupa. 4 kąt między krawędzią podstawy, a przekątną ściany bocznej. 5 kąt między krawędzią ściany bocznej, a krawędzią podstawy. 6 kąt między krawędzią ściany bocznej, a przekątną ściany bocznej. Poprzedni Dalej

Slide 5

Budynek w kształcie graniastosłupa Powrót Dalejc

Slide 6

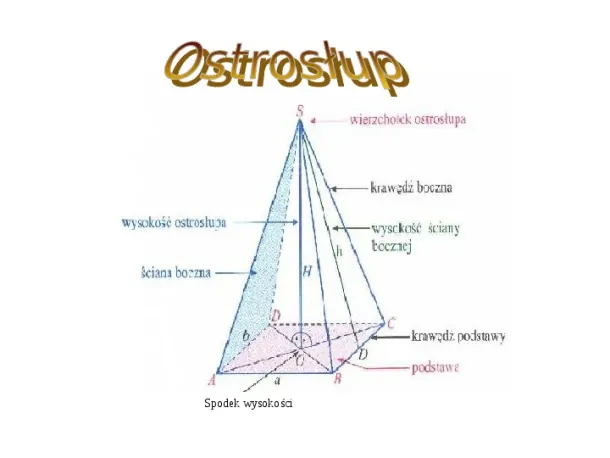
Ostrosłupy Ostrosłupem nazywamy wielościan, którego jedna ściana, zwana podstawą jest dowolnym wielokątem, a pozostałe ściany, zwane ścianami bocznymi, są trójkątami o wspólnym wierzchołku S, który nazywamy wierzchołkiem ostrosłupa. Rodzaje ostrosłupów :  Ostrosłup prawidłowy - jego podstawa jest wielokąt foremny, a ścianami bocznymi przystające  trójkąty foremne.  Czworościan - ostrosłup o podstawie trójkąta. Czworościan, którego wszystkie ściany są trójkątami równobocznymi nazywamy czworościanem foremnym.  Ostrosłup ścięty - część ostrosłupa zawarta między płaszczyzną jego podstawy, a równoległa do niej płaszczyzna przechodzącą przez jego punkt wewnętrzny. Powrót Dalej

Slide 7

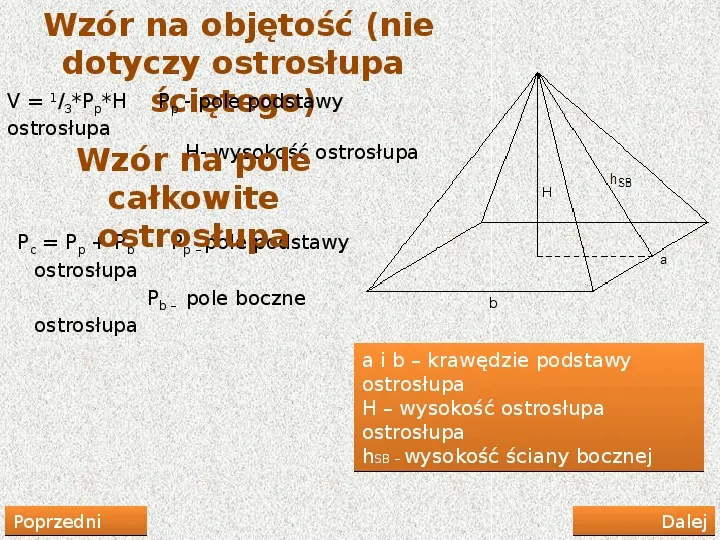
 Wzór na objętość (nie dotyczy ostrosłupa V P H     P - pole podstawy ściętego) 1 3 p p ostrosłupa                             H- wysokość ostrosłupa Wzór na pole całkowite  P P ostrosłupa P P pole podstawy c p b p ostrosłupa Pb pole boczne ostrosłupa a i b krawędzie podstawy ostrosłupa H wysokość ostrosłupa ostrosłupa hSB wysokość ściany bocznej Poprzedni Dalej

Slide 8

Budynek w kształcie ostrosłupa Powrót Dalej

Slide 9

Bryły obrotowe Bryła obrotowa - są to bryły powstałe w wyniku obrotu brył płaskich wokół własnej osi. Najważniejsze bryły obrotowe : Walec - bryła powstała w wyniku obrotu prostokąta wokół jednej z krawędzi. Stożek - bryła powstała w wyniku obrotu trójkąta prostokątnego wokół przyprostokątnej. Kula - bryła powstała w wyniku obrotu koła wokół jego średnicy. Powrót Dalej

Slide 10

Wzór na objętość V π r walca h 2 Wzór na pole całkowite walca  Pc 2Pp Pb P p   π r 2 Pb 2 π r h Pp pole podstawy walca Pb pole boczne walca Poprzedni  r - promień podstawy h - wysokość  walca Dalej

Slide 11

Wzór na objętość stożka V 13Pp h Wzór na pole całkowite stożka    Pc Pp Pb Pp π r2 Pb π r l Pp - pole podstawy stożka Pb - pole boczne stożka Poprzedni l - tworząca stożka r promień stożka h - wysokość stożka Dalej

Slide 12

Wzór na objętość kuli V 43π r3 Wzór na pole całkowite kuli P 4π r2 Poprzedni r - promień kuli Dalej

Slide 13

dynki w kształcie brył obrotow Powrót Dalej

Slide 14

Źródł a http:www.zarzadca.bizvarzarzadcastorageimagesofirmienierucho moscibudynekbiurowyulbokserska660-2-polPLbudynekbiurowyulbokserska.jpg http:matematyka.plpublicgeometriaprostopadloscian.png http:www.bazywiedzy.comgfxostroslup-prawidlowy-czworokatny.png http:www.math.edu.plgraniastoslupy http:matma.prv.plgraniastoslupy.php http:figuryprzestrzenne.webpark.plgraniastoslup.htmldefinicja http:sisi.ovh.orgindexmatmaniezbednikbryly.html http:matma.prv.plostroslupy.php http:www.math.edu.plostroslupy http:figuryprzestrzenne.webpark.plostroslup.html http:wersus.com.pl200620obrazkiMatgimKatywostoslupie.jpg http:zyrardow.pttk.plglobtroterpicturespiramida.jpg http:wa5.www.artehistoria.jcyl.escivilizacionesjpgBAM15545.jpg http:www.viajesyviajeros.comsamarcanda6.jpg http:www.math.edu.plimagesgeometriastozek.gif http:www.matematyka-marta.yoyo.plimageswalec02.png www.google.com Powrót Dalej

Slide 15

Dziękuję za uwagę Wykonała Małgorzata Grochowska z klasy 3a Powrót