Bazy danych

Zobacz slidy

Treść prezentacji

Slide 1

Bazy danych Wykład (12 godz): Jan Aleksander Wierzbicki Ćwiczenia (20 15 godz): Jan Aleksander Wierzbicki

Slide 2

Zaliczenie przedmiotu obecność na zajęciach ćwiczeniawykład rozwiązywanie prac domowych egzamin część teoretyczna część praktyczna na podstawie prac domowych przygotowanie własnej aplikacji Bazy Danych

Slide 3

Literatura Lech Banachowski: Bazy danych projektowanie aplikacji, Akademicka OficynaWydawnicza PLJ, 1998 Dariusz Boratyn: MS Access97, Croma, 1997 Paul Beynon-Davies: Systemy baz danych, WNT, 1998

Slide 4

Baza danych pojęcie sięgające wieków informacja pewien zasób ludzie od zawsze próbują gromadzić informację i wnioskować na jej podstawie komputery tylko ułatwiają przetwarzanie informacji

Slide 5

Informacja ma wartość gdy jest: dokładna (nie za dużo, ani nie za mało) dostępna gdy mamy zły sposób poszukiwania informacji możemy nie być wstanie jej odszukać - może nam zabraknąć np. życia - komputer tu nic nie pomoże

Slide 6

Baza danych metoda strukturalizacji zarządzania informacją dotyczy fragmentu rzeczywistości i stanowi kolekcję danych część systemu informacyjnego - aplikacja bazy danych (oprogramowanie) - system informatyczny (sprzęt)

Slide 7

Linia lotnicza D B E A C F

Slide 8

Inne złożone Bazy danych Bankowe ochrona danych Satelitarne tryliardy danych

Slide 9

Cechy bazy danych trwałość (aplikacja powinna działać przez długi okres czasu dane przechowywane latami) zgodność z rzeczywistością zmiana rzeczywistości musi być uwzględniona w bazie danych

Slide 10

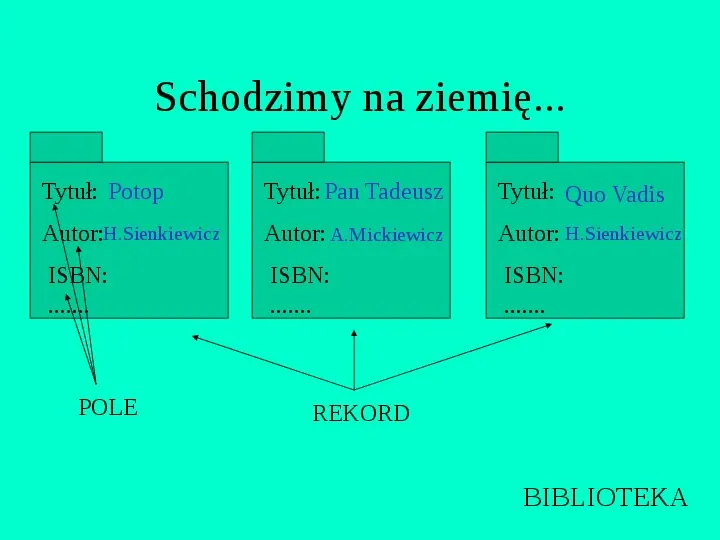
Schodzimy na ziemię... Tytuł: Potop Tytuł: Pan Tadeusz Tytuł: Quo Vadis Autor:H.Sienkiewicz Autor: A.Mickiewicz Autor: H.Sienkiewicz ISBN: ....... ISBN: ....... ISBN: ....... POLE REKORD BIBLIOTEKA

Slide 11

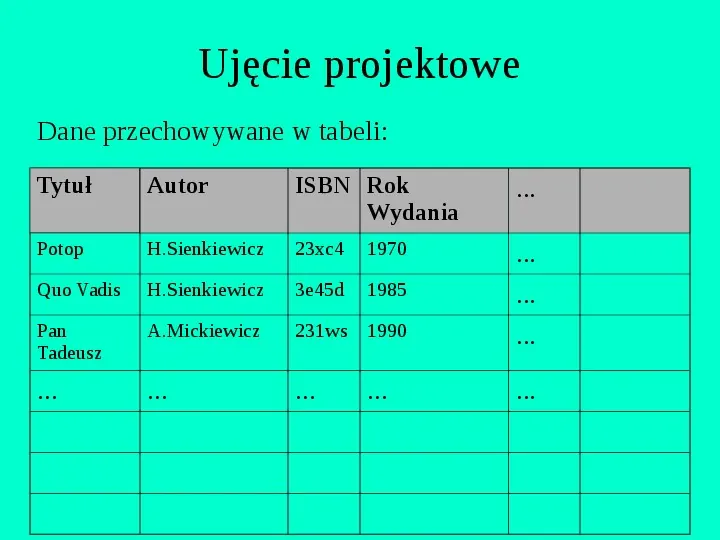
Ujęcie projektowe Dane przechowywane w tabeli: Tytuł Autor ISBN Rok Wydania ... Potop H.Sienkiewicz 23xc4 1970 Quo Vadis H.Sienkiewicz 3e45d 1985 Pan Tadeusz A.Mickiewicz 231ws 1990 ... ... ... ... ... ... ... ...

Slide 12

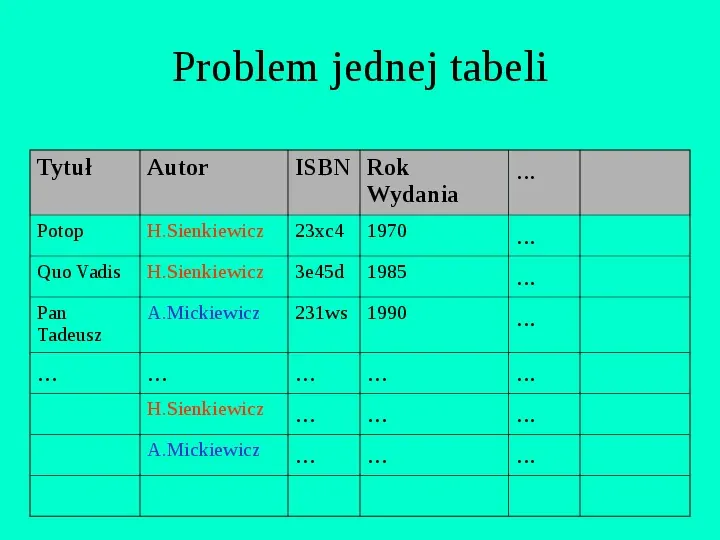
W bazie danych, musimy kontrolować redundancję (powtarzanie się danych) jeden fakt powinien być reprezentowany na jeden sposób problem dostępności i dokładności poszukiwanych danych (czas dostępu oraz nadmiar danych)

Slide 13

Problem jednej tabeli Tytuł Autor ISBN Rok Wydania ... Potop H.Sienkiewicz 23xc4 1970 Quo Vadis H.Sienkiewicz 3e45d 1985 Pan Tadeusz A.Mickiewicz 231ws 1990 ... ... ... ... ... ... ... ... ... ... ... H.Sienkiewicz A.Mickiewicz ... ... ...

Slide 14

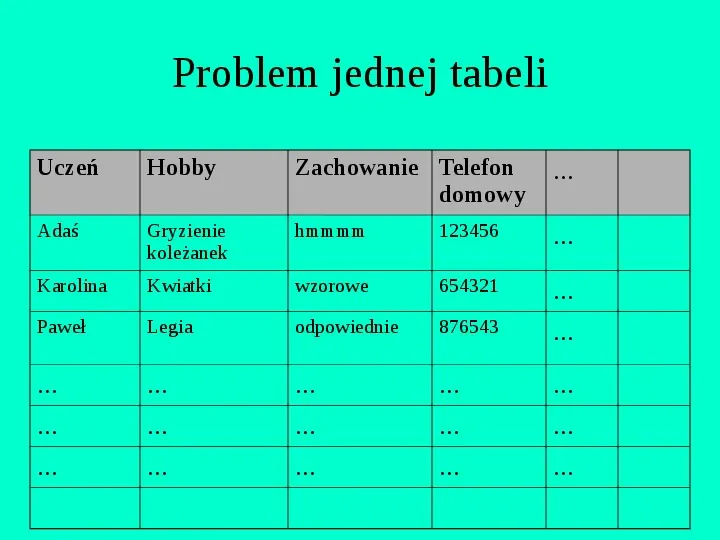
Problem jednej tabeli Uczeń Hobby Zachowanie Telefon domowy ... Adaś Gryzienie koleżanek hmmmm 123456 ... Karolina Kwiatki wzorowe 654321 Paweł Legia odpowiednie 876543 ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...

Slide 15

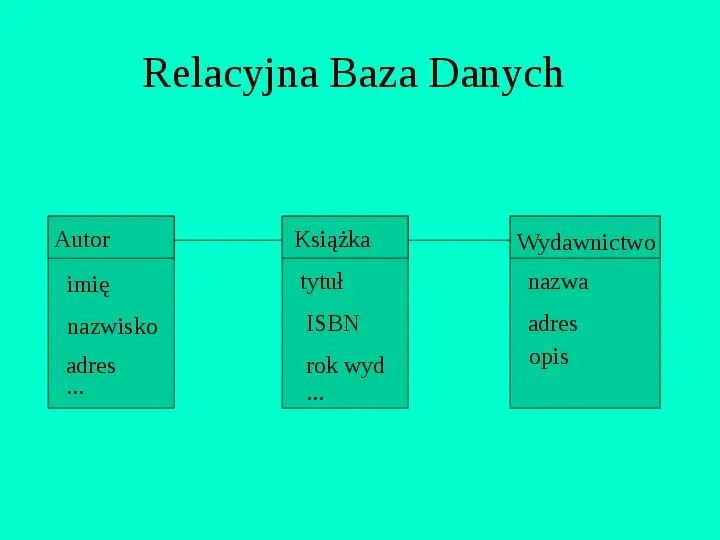
Relacyjna Baza Danych Autor Książka Wydawnictwo imię tytuł nazwa nazwisko ISBN adres ... rok wyd ... adres opis

Slide 16

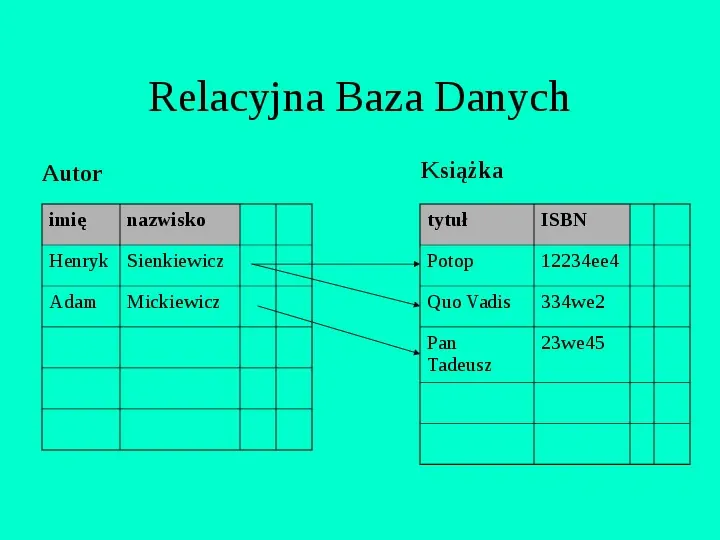
Relacyjna Baza Danych Książka Autor imię nazwisko tytuł ISBN Henryk Sienkiewicz Potop 12234ee4 Adam Quo Vadis 334we2 Pan Tadeusz 23we45 Mickiewicz

Slide 17

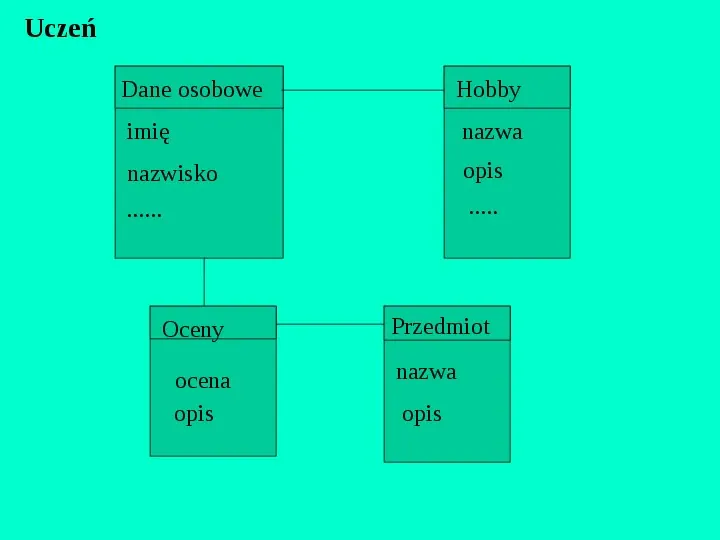
Uczeń Dane osobowe Hobby imię nazwa nazwisko ...... opis ..... Oceny ocena opis Przedmiot nazwa opis

Slide 18

Jak budujemy bazę danych? przyrostowy - dla każdego elementu osobna baza, potem próba łączenia - wada brak globalnej wizji (redundancja, niespójność) zintegrowany system

Slide 19

Budując bazę, bierzemy pod uwagę: jeden system (model) reprezentacji danych np. model relacyjny współbieżny dostęp do bazy przez wielu użytkowników ochrona danych niezależność (zależność) określonych danych

Slide 20

Aplikacje korzystają z bazy: poprzez model danych zbiór zasad dotyczących struktur danych, warunki wspomagające utrzymanie zgodności z rzeczywistością system zarządzania bazą danych zbiór narzędzi dających dostęp do danych i ich aktualizacji np. wyszukiwanie danych, ochrona i dostęp do danych, konta użytkowników

Slide 21

Modelowanie danych specyfikacja wymagań użytkowników określenie modelu systemowego konfiguracja sprzętu i oprogramowania projektowanie bazy 80 czasu tworzenia implementacja bazy 20 czasu tworzenia

Slide 22

Relacyjny model danych twórca E.F.Codda (1970) terminologia matematyczna baza danych to zbiór relacji relacja jest reprezentowana przez tablicę (kolumny i wiersze) np. dla zadanej kolumny mamy w wierszu odpowiednią wartość

Slide 23

Posługiwanie się bazą danych wyszukiwanie danych modyfikacja (aktualizacja) danych dopisywanie danych usuwanie danych

Slide 24

Baza danych na przykładzie Microsoft Access płaszczyzna projektanta płaszczyzna użytkownika wyszukiwanie, modyfikacja, dopisywanie, usuwanie danych w obu płaszczyznach na podstawie mechanizmów płaszczyzny projektanta możliwe jest tworzenie płaszczyzny użytkownika (interfejs użytkownika)

Slide 25

Wyszukiwanie danych filtr doraźnie kwerenda trwale