Wlasności figur plaskich

Zobacz slidy

Treść prezentacji

Slide 2

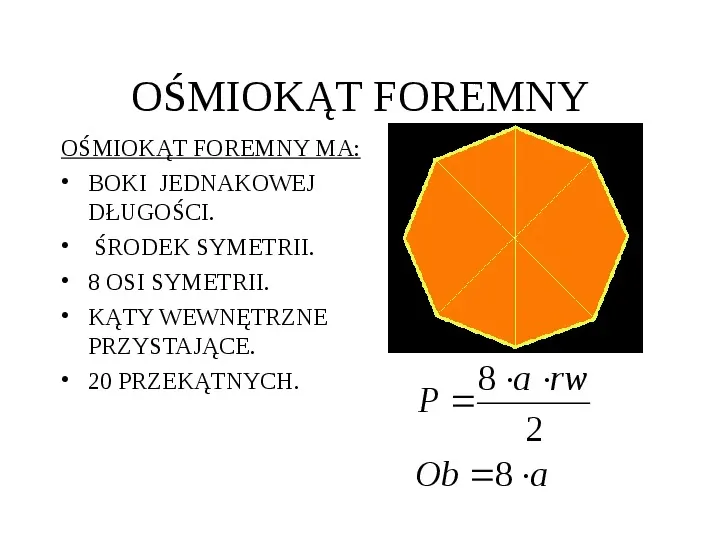
OŚMIOKĄT FOREMNY OŚMIOKĄT FOREMNY MA: BOKI JEDNAKOWEJ DŁUGOŚCI. ŚRODEK SYMETRII. 8 OSI SYMETRII. KĄTY WEWNĘTRZNE PRZYSTAJĄCE. 20 PRZEKĄTNYCH. 8 a rw P 2 Ob 8 a

Slide 3

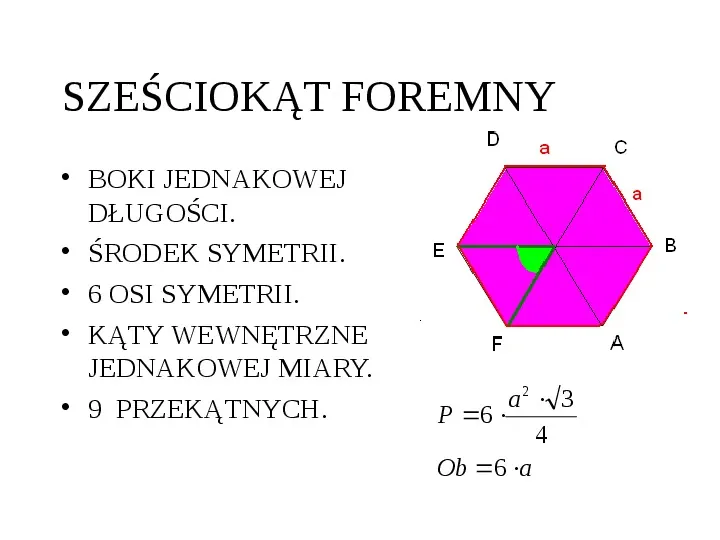
SZEŚCIOKĄT FOREMNY BOKI JEDNAKOWEJ DŁUGOŚCI. ŚRODEK SYMETRII. 6 OSI SYMETRII. KĄTY WEWNĘTRZNE JEDNAKOWEJ MIARY. 9 PRZEKĄTNYCH. a2 3 P 6 4 Ob 6 a

Slide 4

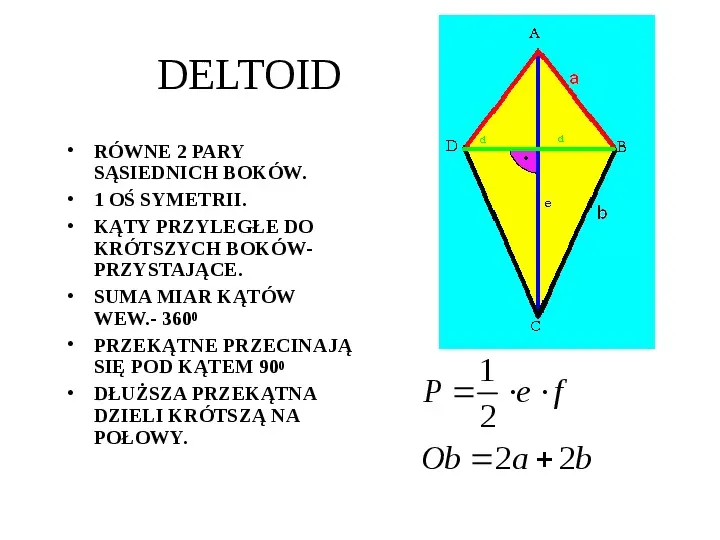
DELTOID RÓWNE 2 PARY SĄSIEDNICH BOKÓW. 1 OŚ SYMETRII. KĄTY PRZYLEGŁE DO KRÓTSZYCH BOKÓWPRZYSTAJĄCE. SUMA MIAR KĄTÓW WEW.- 3600 PRZEKĄTNE PRZECINAJĄ SIĘ POD KĄTEM 900 DŁUŻSZA PRZEKĄTNA DZIELI KRÓTSZĄ NA POŁOWY. 1 P e f 2 Ob 2a 2b

Slide 5

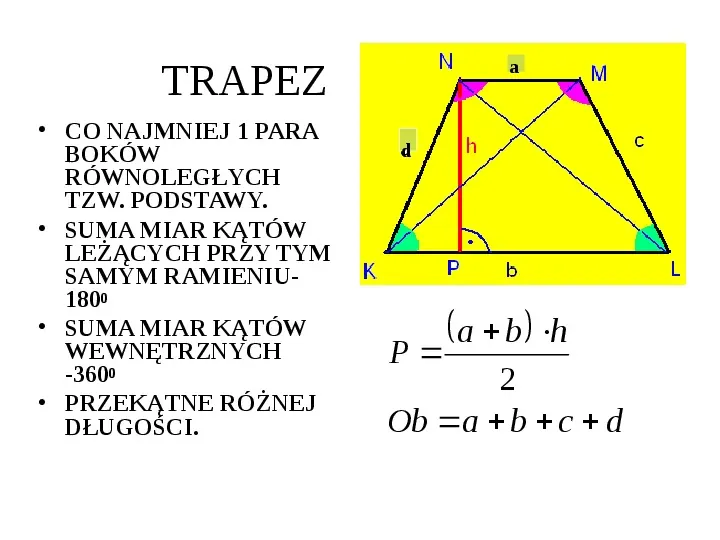
a TRAPEZ CO NAJMNIEJ 1 PARA BOKÓW RÓWNOLEGŁYCH TZW. PODSTAWY. SUMA MIAR KĄTÓW LEŻĄCYCH PRZY TYM SAMYM RAMIENIU1800 SUMA MIAR KĄTÓW WEWNĘTRZNYCH -3600 PRZEKĄTNE RÓŻNEJ DŁUGOŚCI. d a b h P 2 Ob a b c d

Slide 6

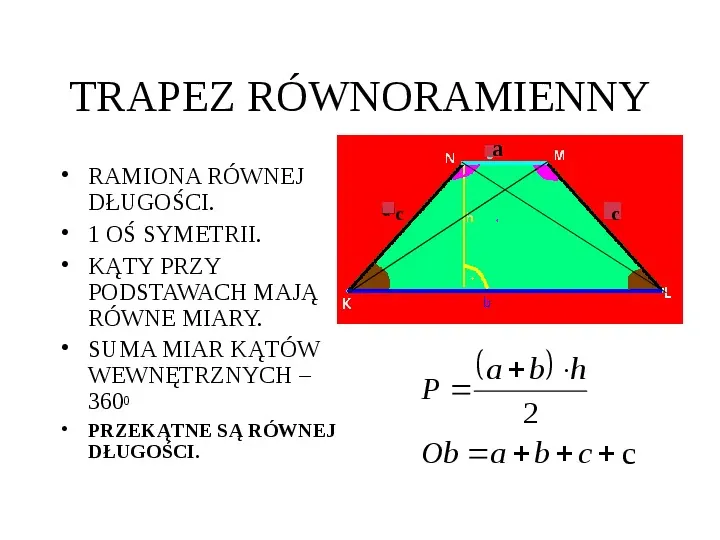
TRAPEZ RÓWNORAMIENNY RAMIONA RÓWNEJ DŁUGOŚCI. 1 OŚ SYMETRII. KĄTY PRZY PODSTAWACH MAJĄ RÓWNE MIARY. SUMA MIAR KĄTÓW WEWNĘTRZNYCH 3600 PRZEKĄTNE SĄ RÓWNEJ DŁUGOŚCI. a c c a b h P 2 Ob a b c dc

Slide 7

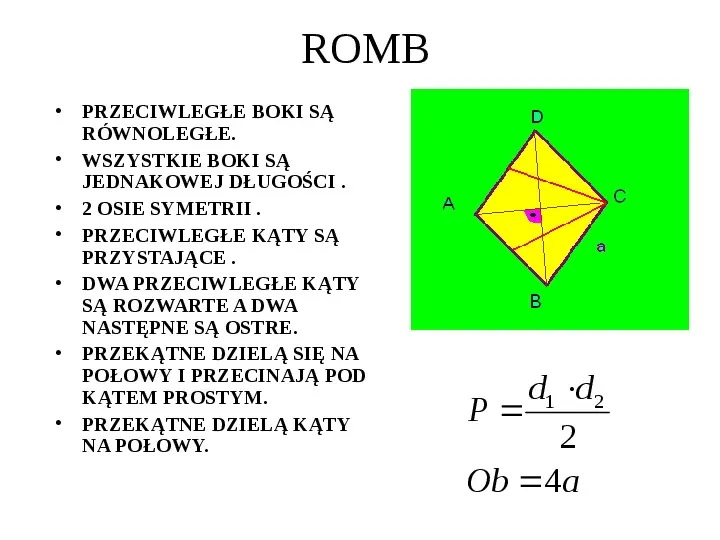
ROMB PRZECIWLEGŁE BOKI SĄ RÓWNOLEGŁE. WSZYSTKIE BOKI SĄ JEDNAKOWEJ DŁUGOŚCI . 2 OSIE SYMETRII . PRZECIWLEGŁE KĄTY SĄ PRZYSTAJĄCE . DWA PRZECIWLEGŁE KĄTY SĄ ROZWARTE A DWA NASTĘPNE SĄ OSTRE. PRZEKĄTNE DZIELĄ SIĘ NA POŁOWY I PRZECINAJĄ POD KĄTEM PROSTYM. PRZEKĄTNE DZIELĄ KĄTY NA POŁOWY. d1 d 2 P 2 Ob 4a

Slide 8

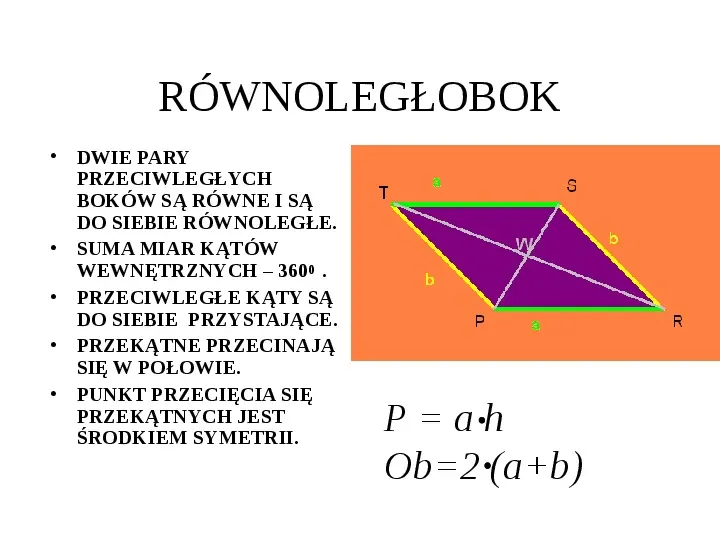
RÓWNOLEGŁOBOK DWIE PARY PRZECIWLEGŁYCH BOKÓW SĄ RÓWNE I SĄ DO SIEBIE RÓWNOLEGŁE. SUMA MIAR KĄTÓW WEWNĘTRZNYCH 3600 . PRZECIWLEGŁE KĄTY SĄ DO SIEBIE PRZYSTAJĄCE. PRZEKĄTNE PRZECINAJĄ SIĘ W POŁOWIE. PUNKT PRZECIĘCIA SIĘ PRZEKĄTNYCH JEST ŚRODKIEM SYMETRII. Pah Ob2 (ab)

Slide 9

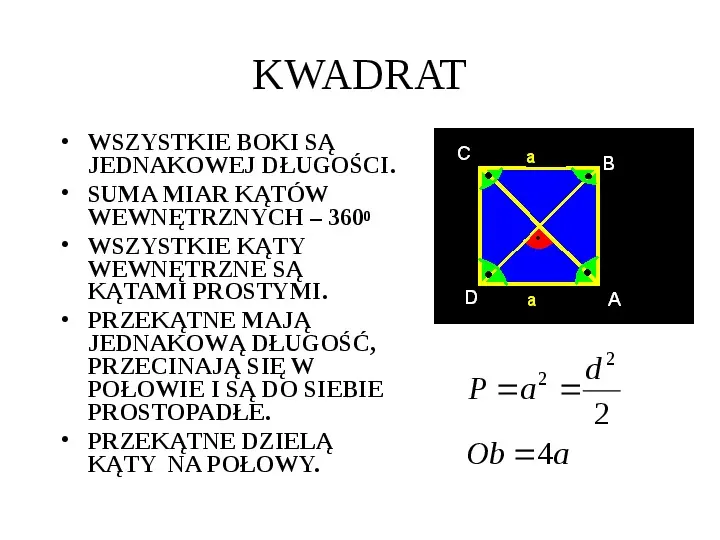
KWADRAT WSZYSTKIE BOKI SĄ JEDNAKOWEJ DŁUGOŚCI. SUMA MIAR KĄTÓW WEWNĘTRZNYCH 3600 WSZYSTKIE KĄTY WEWNĘTRZNE SĄ KĄTAMI PROSTYMI. PRZEKĄTNE MAJĄ JEDNAKOWĄ DŁUGOŚĆ, PRZECINAJĄ SIĘ W POŁOWIE I SĄ DO SIEBIE PROSTOPADŁE. PRZEKĄTNE DZIELĄ KĄTY NA POŁOWY. 2 d P a 2 2 Ob 4a

Slide 10

PROSTOKĄT BOKI SĄ PARAMI RÓWNE I RÓWNOLEGŁE. SUMA MIAR KĄTÓW WEWNĘTRZNYCH 3600 . WSZYSTKIE KĄTY SĄ PROSTE. PRZEKĄTNE MAJĄ JEDNAKOWĄ DŁUGOŚĆ, PRZECINAJĄ SIĘ W POŁOWIE. PUNKT PRZECIĘCIA PRZEKĄTNYCH JEST ŚRODKIEM OKRĘGU OPISANEGO NA PROSTOKĄCIE. Pab Ob2 (ab)

Slide 11

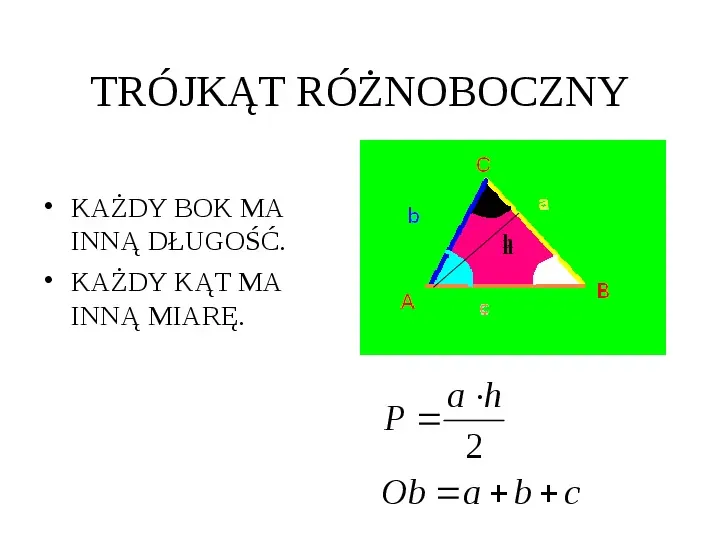
TRÓJKĄT RÓŻNOBOCZNY KAŻDY BOK MA INNĄ DŁUGOŚĆ. KAŻDY KĄT MA INNĄ MIARĘ. h h a h P 2 Ob a b c

Slide 12

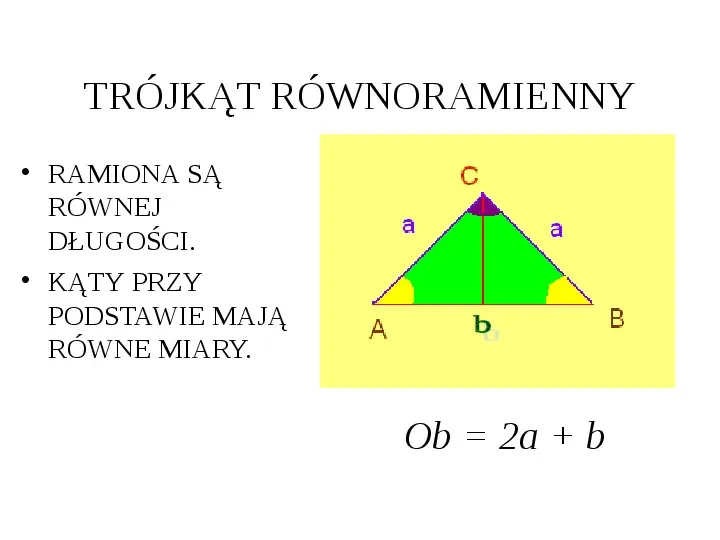
TRÓJKĄT RÓWNORAMIENNY RAMIONA SĄ RÓWNEJ DŁUGOŚCI. KĄTY PRZY PODSTAWIE MAJĄ RÓWNE MIARY. Ob 2a b

Slide 13

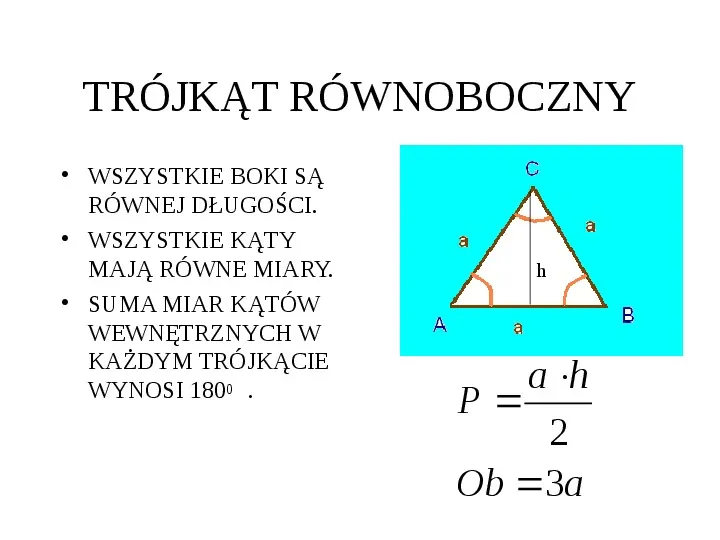
TRÓJKĄT RÓWNOBOCZNY WSZYSTKIE BOKI SĄ RÓWNEJ DŁUGOŚCI. WSZYSTKIE KĄTY MAJĄ RÓWNE MIARY. SUMA MIAR KĄTÓW WEWNĘTRZNYCH W KAŻDYM TRÓJKĄCIE WYNOSI 1800 . h a h P 2 Ob 3a