Liczba PI

Zobacz slidy

Treść prezentacji

Slide 1

Adam Wystop Mateusz Kowalczyk

Slide 2

Historia Szacowana wartość Wzory Kuć i orać Wyjście

Slide 3

Wzory z zastosowaniem liczby Długość okręgu: l 2r r promień Przykład Pole koła: Ł 2r 360 r promień Przykład Pole wycinka kołowego: P r2 r promień Długość łuku: Przykład P 2 r 360 r promień Powrót Przykład Dalej

Slide 4

Wzory z zastosowaniem liczby Objętość kuli: 4 3 V r 3 Obwód elipsy: a b O 3 2 ab r promień Przykład Pole elipsy: P ab a długości osi wielkiej b długości osi małej Przykład Powrót a długości osi wielkiej b długości osi małej Przykład Pole powierzchni kuli: P 4r 2 r promień Przykład

Slide 5

Długość okręgu przykład. r Dla r 3 l 2r l 2 3 l 6 18,84 Powrót

Slide 6

Pole koła przykład. r Dla r 3 P r 2 P 32 P 9 28,26 Powrót

Slide 7

Długość łuku przykład. r Dla r 3 i α 90o Ł 2r 360 90 Ł 2 3 360 1 Ł 2 3 4 1 Ł 1 4,71 2 Powrót

Slide 8

Pole wycinka kołowego przykład. r Dla r 3 i α 90o 2 P r 360 90 2 P 3 360 1 P 9 4 1 P 2 4,71 4 Powrót

Slide 9

Objętość kuli przykład. r Dla r 3 V V V V 4 3 r 3 4 3 3 3 4 27 3 36 113,04 Powrót

Slide 10

Pole powierzchni kuli przykład. r Dla r 3 P 4r 2 P 4 32 P 36 113,04 P 36 113,04 Powrót

Slide 11

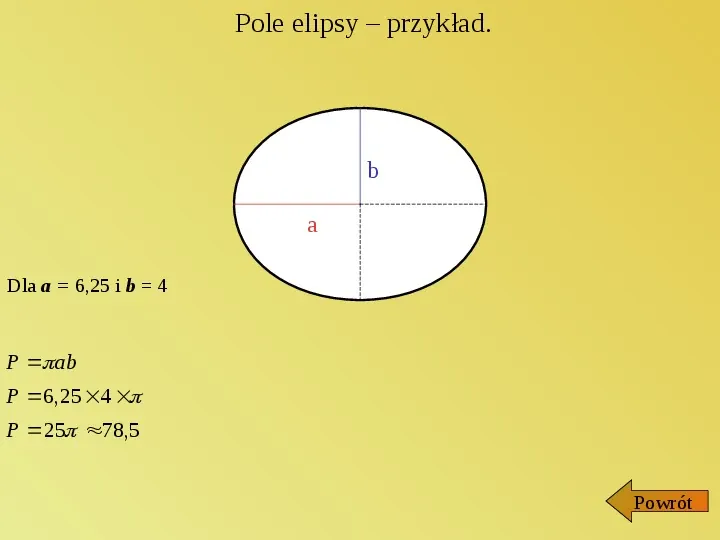
Pole elipsy przykład. b a Dla a 6,25 i b 4 P ab P 6,25 4 P 25 78,5 Powrót

Slide 12

Obwód elipsy przykład. Dla a 6,25 i b 4 a b O 3 ab 2 6,25 4 O 3 6,25 4 2 10,25 O 3 25 2 6,25 4 O 3 6,25 4 2 O 3 5,125 5 O 15,375 5 O 10,375 32,5775 b a Powrót

Slide 13

Liczba (ludolfina) Liczba pi jest liczbą niewymierną określająca stosunek długości okręgu do jego średnicy. Długośćśrednica 3,14159265358979323846264338327950288419716939937510... Symbol wprowadzony w 1706 r. przez angielskiego matematyka Wiliama Jonesa w powszechne użycie wszedł dopiero w połowie XVIII wieku po wydaniu Analizy L. Eulera. Liczba jest niewymierna. Określa się ją często ludolfiną. Nazwa ta pochodzi od imienia holenderskiego matematyka Ludolfa van Ceulena, który w 1610 r. obliczył wartość liczby π z dokładnością do 35 cyfr po przecinku. Przełomową w historii liczby π datą był rok 1882, w którym matematyk niemiecki F. Lindemann udowodnił ostatecznie, że liczba π jest liczbą przestępną (to znaczy, że nie może ona być pierwiastkiem równania algebraicznego o współczynnikach całkowitych). Wykazał on w ten sposób nierozwiązalność słynnego w starożytności zagadnienia kwadratury koła. Interesująca jest historia tej liczby. Oto najważniejsze jej oszacowania: Dalej

Slide 14

Szacowana wartość liczby na przestrzeni dziejów. Babilończycy (ok. 2000 r. p.n.e.) Egipcjanie (ok. 2000 r. p.n.e.) 3 16 9 2 Archimedes (III w. p.n.e.) matematyk i fizyk grecki 22 7 10 10 3 3 71 70 Klaudiusz Ptolemeusz (II w. n.e.) - matematyk grecki 8 30 3 60 3600 Alchwarizmi (IX w.) uczony arabski 10 Dalej

Slide 15

Szacowana wartość liczby na przestrzeni dziejów. Powrót Bhâskara (XII w.) słynny matematyk hinduski 754 240 A. Metius (rok 1585) matematyk i astronom holenderski 355 113 Dalej

Slide 16

Kolejne cyfry rozwinięcia dziesiętnego. Zazwyczaj przy obliczeniach technicznych przyjmujemy 3,1416 lub 3,14  zależnie od wymaganego stopnia dokładności. W robotach blacharskich, kotlarskich itp. przy wyznaczaniu obwodu koła przyjmujemy 227. Obecnie za pomocą elektronicznych maszyn cyfrowych obliczono milion cyfr rozwinięcia liczby . W praktyce jednak całkowicie wystarcza znajomość 8 cyfr rozwinięcia dziesiętnego 3.14159265358979323846264338327950288419716939937510582097494459230781 6406286208998628034825342117067982148086513282306647093844609550582231 7253594081284811174502841027019385211055596446229489549303819644288109 7566593344612847564823378678316527120190914564856692346034861045432664 8213393607260249141273724587006606315588174881520920962829254091715364 3678925903600113305305488204665213841469519415116094330572703657595919 5309218611738193261179310511854807446237996274956735188575272489122793 8183011949129833673362440656643086021394946395224737190702179860943702 7705392171762931767523846748184676694051320005681271452635608277857713 427577896091736371787214684409012249534301465495853... Dalej

Slide 17

Kuć i orać Popularna była dawniej mnemotechnika liczby (układanie wierszy lub innych tekstów, w których liczby liter poszczególnych słów są identyczne z zajmującymi to samo miejsce cyframi w rozwinięciu tej liczby). Znany jest np. wiersz A. Cwojdzińskiego: Kuć i orać w dzień zawzięcie, bo plonów nie-ma bez trudu złocisty szczęścia okręcie kołyszesz... Kuć. My nie czekamy cudu Robota to potęga ludu. Liczba poszczególnych słów tego wiersza jest rozwinięciem liczby : 3,141 592 653 589 793 238 462 643... Powrót

Slide 18

Dziękujemy za obejrzenie prezentacji! Autorzy: Adam Wystop, Mateusz Kowalczyk Bibliografia: Encyklopedia szkolna : matematyka. Do zobaczenia ! Wydaw. Szkolne i Pedagogiczne, 2003. INTERNET: www.matematyka.prx.pl www.republika.plbizmut83 KONIEC