Fizyka starożytna: dwie metody pomiaru odległości Słońca od Ziemi

Zobacz slidy

Treść prezentacji

Slide 1

Jakub Bilski Koło Naukowe Fizyków Migacz Uniwersytet Wrocławski Fizyka starożytna: dwie metody pomiaru odległości Słońca od Ziemi Fizyczno filozoficzna analiza nauki hellenistycznej

Slide 2

I Zarys myślenia greckiego

Slide 3

Natura widziana oczami Greka Na początku była filozofia przyrody Pitagorejska matematyzacja przyrody od praktyki do teorii Idealizacja myślenia odejście od praktyki; filozofia systemów Metafizyka pierwszą filozofią Fizyka pojmowana jako nauka teoretyczna Aksjomatyczne: religijne i metafizyczne wyjaśnianie przyczyn Ksenokratesa podział filozofii na: fizykę, logikę i etykę

Slide 4

Gdy rozpadły się ściany świata przełom hellenistyczny Okres hellenistyczny: 323 30 p.n.e. Narodziny nauki nowożytnej ukształtowanie się nauk szczegółowych: fizyki, geometrii, historii, medycyny, psychologii Główny ośrodek naukowy: Aleksandria (Biblioteka i Musejon) Zdesakralizowany obraz świata Odrzucenie dedukcyjnego i indukcyjnego modelu badań zastąpionych metodą obserwacji, a nawet (choć zdecydowanie rzadziej) eksperymentu, bez konieczności wyciągania ogólnych wniosków Podział zjawisk na obserwowalne i niejawne czekające na wyjaśnienie Autonomiczny w stosunku do filozofii rozwój nauk szczegółowych technai można było zostać uczonym, nie będąc filozofem Dla nowych szkół filozoficznych zatem wiedza o kosmosie-naturze fizyka stała się metateorią

Slide 5

II Astrometria hellenistyczna

Slide 6

Arystarch z Samos ok. 320 250 p.n.e. Twórca teorii heliocentrycznej Jedyne zachowane dzieło: O rozmiarach i odległościach Słońca i Księżyca

Slide 7

Obserwacje Arystarcha Księżyc odbija światło słoneczne Ziemia jest środkiem sfery Księżyca W czasie kwadry koło wielkie rozdzielające jasną i ciemną stronę księżyca leży w płaszczyźnie przechodzącej przez obserwatora W czasie kwadry odległość (kątowa) Księżyca od Słońca jest mniejsza od czwartej części okręgu (ekliptyki) o 130 jego część Szerokość cienia Ziemi obejmuje dwa Księżyce Tarcza Księżyca i tarcza Słońca obejmują 150 część Zodiaku (36)

Slide 8

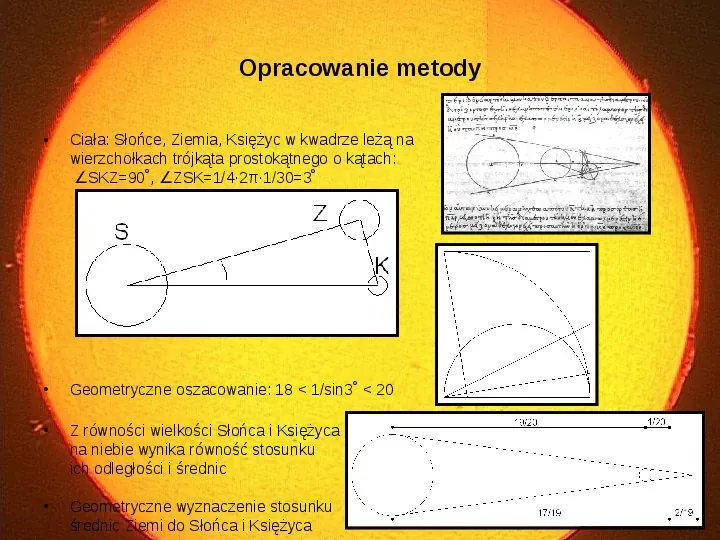
Opracowanie metody Ciała: Słońce, Ziemia, Księżyc w kwadrze leżą na wierzchołkach trójkąta prostokątnego o kątach: SKZ90, ZSK142π1303 Geometryczne oszacowanie: 18 1sin3 20 Z równości wielkości Słońca i Księżyca na niebie wynika równość stosunku ich odległości i średnic Geometryczne wyznaczenie stosunku średnic Ziemi do Słońca i Księżyca

Slide 9

Otrzymane wyniki Odległość Księżyca od Ziemi: 9,5 d Odległość Ziemi od Słońca: 180 d Średnica Księżyca: 0,36 d Średnica Słońca: 6,75 d [30,2 d] [11726 d] [0,27 d] [108,9 d] Odległości podane w średnicach Ziemi d W nawiasach podano średnie wielkości zmierzone obecnie Taka notacja będzie kontynuowana w dalszej części

Slide 10

Eratostenes z Cyreny ok. 276 194 p.n.e. Zarządca biblioteki Aleksandryjskiej (ok. 246 197 p.n.e.) Twórca mapy znanego świata opartej na współrzędnych sferycznych (od Gibraltaru po Indie i od Somalii do północnego koła podbiegunowego) Podał sposób znajdowania liczb pierwszych (sito Eratostenesa) Wyznaczył kąt nachylenia Ziemi do orbity: 1183 (23,9) [23,4] Wyznaczył kąt nachylenia ekliptyki do równika niebieskiego Stworzył katalog 675 gwiazd stałych Precyzyjnie zmierzył długość Ziemskiego południka

Slide 11

Pomiary Eratostenesa Wyznaczenie położenia Syene na zwrotniku Wyznaczenie odległości między Aleksandrią a Syene: 150 łuku (7,2) Najsłynniejszy eksperyment starożytnej fizyki pomiar długości południka: 252000 stadionów

Slide 12

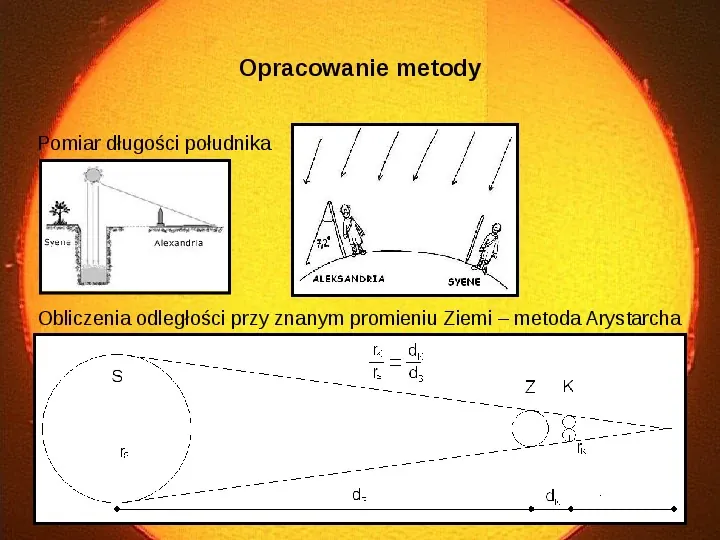
Opracowanie metody Pomiar długości południka Obliczenia odległości przy znanym promieniu Ziemi metoda Arystarcha

Slide 13

Otrzymane wyniki Długość południka: 252000 stadionów (39700 km lub 46600 km) [40000 km] Odległość Ziemi od Słońca: 804mln stadionów, czyli 10023 d (126,6mln km lub 148,7mln km) [149,6mln km, czyli 11726 d] Odległość Księżyca od Ziemi: 780000 stadionów, czyli 9,7 d (122900 km lub 144300 km) [384400 km, czyli 30,2 d] Licząc dalej tą samą metodą otrzymamy: Średnica Księżyca: ok. 40000 stadionów, czyli ok. 0,5 d Średnica Słońca: ok. 41mln stadionów, czyli ok. 500 d [0,27 d] [108,9 d]

Slide 14

Świadectwa doksograficzne wcześniejszych pomiarów Arystoteles: Dzięki badaniom astronomów stało się wiadome, że [Ziemia] jest wielokroć mniejsza od niektórych gwiazd. () Byłoby bowiem rzeczą zbyt uproszczoną sądzić, iż każde spośród poruszających się ciał jest niewielkie, bo tak wydaje się nam obserwującym z dołu. Ci spośród matematyków, którzy starają się obliczyć wielkość obwodu Ziemi, dochodzą do miary 400000 stadiów. () [J]ak wynika z obliczeń astronomów, Słońce przekracza Ziemię wielkością, odległość natomiast gwiazd od Ziemi jest większa niż od Słońca podobnie jak odległość Słońca od Ziemi przewyższa odległość Słońca do Księżyca zatem stożek wyznaczony przez promienie słoneczne zakończy się w niewielkiej odległości od Ziemi i cień Ziemi, który nazywamy nocą, nie przedłuży się do gwiazd.

Slide 15

Astronomiczne sukcesy Hipparcha ok. 190125 p.n.e. Zmierzenie paralaksy Księżyca Odkrycie precesji punktów równonocy i dostrzeżenie nierównej długości pór roku Zauważenie perturbacji w ruchu Księżyca Stworzenie katalogu 1080 gwiazd stałych Hipoteza powolnego ruchu gwiazd stałych, niedostrzegalnego w czasie życia Opisanie siły ciążenia zależnej od odległości do centrum Ziemi Model procy (tak nazwie go Posejdonios) argument z równowagi siły ciężkości i siły dośrodkowej za ruchem Księżyca i planet po kołowych orbitach mających jako centrum odpowiednio: Ziemię i Słońce Zestawienie kilku pomiarów Hipparcha: Odległość Księżyca od Ziemi: 33,6 d [30,2 d] Odległość Ziemi od Słońca: 1245 d [11726 d] Średnica Księżyca: 0,33 d [0,27 d] Średnica Słońca: 12,33 d [108,9 d]

Slide 16

Metoda Posejdoniosa ok. 135 50 p.n.e. Związanie pływów z oddziaływaniem Słońca i Księżyca Obliczenie obwodu Ziemi zmodyfikowaną metodą Eratsotenesa (pomiar różnicy wysokości nad horyzontem gwiazdy Canopus w Aleksandrii i na Rodos): 240000 stadionów Sporządzenie mapy znanego świata (wzorowanej na mapie Eratostenesa) Zestawienie kilku pomiarów Posejdoniosa: Odległość Księżyca od Ziemi: 26,2 d [30,2 d] Odległość Ziemi od Słońca: 6545 d [11726 d] Średnica Księżyca: 0,16 d [0,27 d] Średnica Słońca: 39,25 d [108,9 d]

Slide 17

Obliczenia Klaudiusza Ptolemeusza ok. 100 168 n.e. Zestawienie kilku pomiarów Ptolemeusza: Odległość Księżyca od Ziemi: 29,5 d [30,2 d] Odległość Ziemi od Słońca: 605 d [11726 d] Średnica Księżyca: 0,29 d [0,27 d] Średnica Słońca: 5,5 d [108,9 d]

Slide 18

III Komentarz fizyczno - filozoficzny

Slide 19

Zaskakujące wnioski Sprzeczności z codziennie dostrzeganymi zjawiskami Podważenie największego autorytetu Arystotelesa Podważenie prawd religijnych Występowanie w przyrodzie wielkości wielokrotnie większych od obserwowalnych; wartości niewyobrażalnych Występowanie w przyrodzie wielkości nieskończonych Opis odrębnego świata pozaziemskiego zwyczajnymi prawami stosowanymi do opisu przyrody Możliwość przewidywania zjawisk rządzących niezdeterminowanym przez prawa Ziemskie losem ludzi

Slide 20

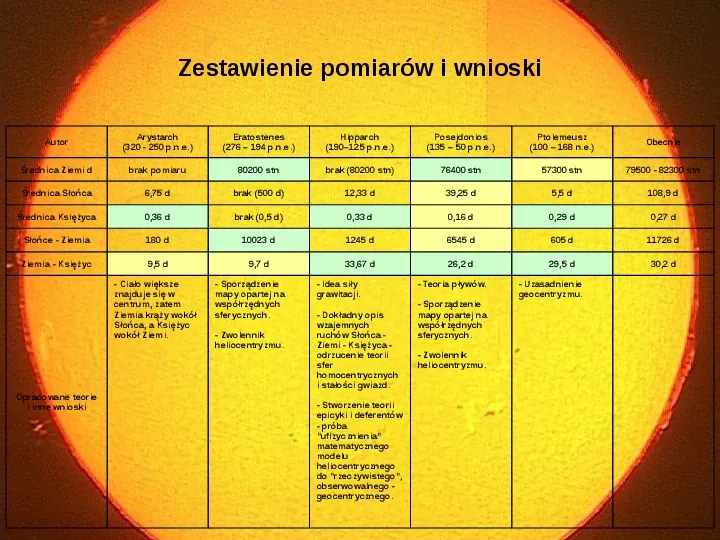
Zestawienie pomiarów i wnioski Autor Arystarch (320 - 250 p.n.e.) Eratostenes (276 194 p.n.e.) Hipparch (190125 p.n.e.) Posejdonios (135 50 p.n.e.) Ptolemeusz (100 168 n.e.) Obecnie Średnica Ziemi d brak pomiaru 80200 stn brak (80200 stn) 76400 stn 57300 stn 79500 - 82300 stn Średnica Słońca 6,75 d brak (500 d) 12,33 d 39,25 d 5,5 d 108,9 d Średnica Księżyca 0,36 d brak (0,5 d) 0,33 d 0,16 d 0,29 d 0,27 d Słońce - Ziemia 180 d 10023 d 1245 d 6545 d 605 d 11726 d Ziemia - Księżyc 9,5 d 9,7 d 33,67 d 26,2 d 29,5 d 30,2 d - Ciało większe znajduje się w centrum, zatem Ziemia krąży wokół Słońca, a Księżyc wokół Ziemi. Opracowane teorie i inne wnioski - Sporządzenie mapy opartej na współrzędnych sferycznych. - Zwolennik heliocentryzmu. - Idea siły grawitacji. - Dokładny opis wzajemnych ruchów Słońca Ziemi - Księżyca odrzucenie teorii sfer homocentrycznych i stałości gwiazd. - Stworzenie teorii epicyki i deferentów - próba ufizycznienia matematycznego modelu heliocentrycznego do rzeczywistego, obserwowalnego geocentrycznego. - Teoria pływów. - Sporządzenie mapy opartej na współrzędnych sferycznych. - Zwolennik heliocentryzmu. - Uzasadnienie geocentryzmu.

Slide 21

Teoria pływów Posejdoniosa Archimedes: Z logicznego dowodu sferycznej siły grawitacji wynika kulistość oceanów nie udaje się wyjaśnić pływów (odkształceń od kulistości) przyczynami występującymi na Ziemi Eratostenes: Morze poziom najwyższy osiąga zazwyczaj niedługo po osiągnięciu przez Księżyc albo najwyższego położenia nad horyzontem, albo położenia po przeciwnej stronie Ziemi Największa różnica między pływami występuje w pobliżu pełni i nowiu Posejdonios: Przyczyną pływów są Księżyc i Słońce Księżyc, położony bliżej Ziemi oddziałuje silniej od Słońca Większa amplituda pływów podczas pełni i nowiu spowodowana jest sumowaniem się oddziaływań Słońca i Księżyca Pływy o największej amplitudzie występują po pełni i nowiu, podobnie do opóźnienia cyklu dobowego woda potrzebuje czasu na przepłynięcie

Slide 22

Teoria heliocentryczna Arystarcha Przyjęcie ruchu obrotowego i wirowego Ziemi nie zniekształca obserwacji Przyjęcie przez analogię ruchu obrotowego dla planet pozwala opisać ich ruch za pomocą kombinacji tylko dwóch jednostajnych ruchów kolistych wokół Słońca Umieszczenie Słońca największego ciała we wszechświecie, w jego centrum, pozwala zachować kosmiczną symetrię Przyjęcie modelu heliocentrycznego pozwala zbudować planetarium (Posejdonios, Archimedes) model tłumaczący ruch Słońca, planet i Księżyca, pozwalający przewidywać ich położenia odpowiadające (jak się okazywało) obserwacjom Późniejsze uzasadnienie Hipparcha: Planety i Księżyc muszą stale krążyć po orbitach kołowych, z niezmienną prędkością analogicznie do działania procy, aby nie spadły na ciało wokół którego krążą, ani nie opuściły orbity Ruch planet można opisać za pomocą epicykli i deferentów, ale przeczy to zasadzie zachowania równowagi procy

Slide 23

Odrzucenie teorii heliocentrycznej Niektóre z konsekwencji ruchu wirowego i obrotowego Ziemi: Podważenie teorii Arystotelesa skonstruowanej na logice dedukcyjnej Ruch z szybkością ponad 1000 kmh (prędkość liniowa śródziemnomorskich szerokości geograficznych) Paralaksa gwiazd stałych Gwiazdy nie znajdują się na sztywnej sferze Argumentacja Arystarcha: Promień orbity ziemskiej ma się tak do promienia sfery gwiazd stałych, jak środek kuli do jej promienia Kontrargumentacja Archimedesa: Nawet niewyobrażalnie duży (mały) stosunek wielkości jednorodnych jest skończony i różny od zera, natomiast stosunek punktu do promienia jest nieskończony (bądź zerowy)

Slide 24

Bibliografia Arystoteles Meteorologika, tłum A. Paciorek, Warszawa 1982. Arystoteles O niebie, tłum. P. Siwek, Warszawa 1980. Janina Gajda Gdy rozpadły się ściany świata, Wrocław 1995. J. J. OConnor, E. F. Robertson Aristarchus of Samos, [dostępne w Internecie:] http:www-history.mcs.st-andrews.ac.ukBiographiesAristarchus.html, [dostęp: 09.11.2010] J. J. OConnor, E. F. Robertson Eratosthenes of Cyrene, [dostępne w Internecie:] http:www-history.mcs.st-andrews.ac.ukBiographiesEratosthenes.html, [dostęp: 09.11.2010] J. J. OConnor, E. F. Robertson Hipparchus of Rhodes, [dostępne w Internecie:] http:www-history.mcs.st-andrews.ac.ukBiographiesHipparchus.html, [dostęp: 09.11.2010] J. J. OConnor, E. F. Robertson Posidonius of Rhodes, [dostępne w Internecie:] http:www-history.mcs.st-andrews.ac.ukBiographiesPosidonius.html, [dostęp: 09.11.2010] Lucio Russo Zapomniana rewolucja, tłum. I. Kania, Kraków 2005. Andrzej K. Wróblewski Historia fizyki, Warszawa 2006.

Slide 25

Dodatek: oszacowanie wartości 1sin3 [19,1] Niech Słońce znajduje się w punkcie A, Ziemia w punkcie B, Księżyc w punkcie C. EBH BAC 3 ; FBE 45 ; GBE 22,5 Stosunek dużego i małego odcinka stycznej do okręgu jest większy od stosunku leżących pod nimi kątów i łuków, stąd: GE HE [904] [9030] 152 FG GE FB BE 2 75 ; FE GE 125 Z powyższego: FE HE (FE GE)(GE HE) (152)(125) 18 BH HE AB BC BE HE FE HE Zatem AB BC 18 Stosunek dużego i małego odcinka cięciwy jest mniejszy od stosunku obejmujących je kątów (DE obejmuje kąt 6, BE2 obejmuje kąt 60), stąd: (BE 2) DE 10 Zatem: BE DE AB BC 20 Ostatecznie: AB BC 19