Fraktale

Zobacz slidy

Treść prezentacji

Slide 1

Fraktale

Slide 2

Fraktale, co to takiego? Termin fraktale jest nowy w języku matematyki, ale figury będące fraktalami konstruowali już bardzo dawno temu wybitni matematycy tacy jak: Peano, Hilbert, a zwłaszcza Sierpiński. Te konstrukcje były im potrzebne głównie po to, aby lepiej wyjaśnić podstawowe pojęcia matematyczne. Co to jest wymiar figury? Co to jest linia?

Slide 3

Teoria fraktali Teoria fraktali , to obecnie bardzo żywo rozwijająca się i bardzo modna dyscyplina. Zajmują się nią specjaliści różnych nauk: matematycy, fizycy, mechanicy. Wielu badaczy twierdzi, że geometria fraktali jest geometrią przyrody. W chmurach, liniach wybrzeży morskich, łańcuchach górskich, płatkach śniegu, drzewach, pianie mydlanej można odkryć kształty fraktali.

Slide 4

Cóż więc to takiego, te fraktale? Fraktale są figurami, w których część figury jest podobna do całości. Ale ciągle jeszcze nie istnieje ścisła definicja fraktala. Najwybitniejszym znawcą fraktali i twórcą tego terminu, jest matematyk i informatyk amerykański Benoit Mandelbrot. W swoim referacie wygłoszonym na Międzynarodowym Kongresie Matematyków w Warszawie w 1983 roku, wypowiedział zdanie, że jest jeszcze za wcześnie na formułowanie ścisłej definicji fraktala, ponieważ ciągle jeszcze nie rozumiemy dostatecznie głęboko istoty tego pojęcia.

Slide 5

. Fraktale mają obecnie swoje miejsce w dziedzinie matematycznej zwanej teorią chaosu. Fraktale są ściśle związane z komputerami. Bez nich nie byłoby możliwe wytworzenie tak wielu przepięknych fraktali, które są swoistymi, jedynymi w swym rodzaju obrazami

Slide 6

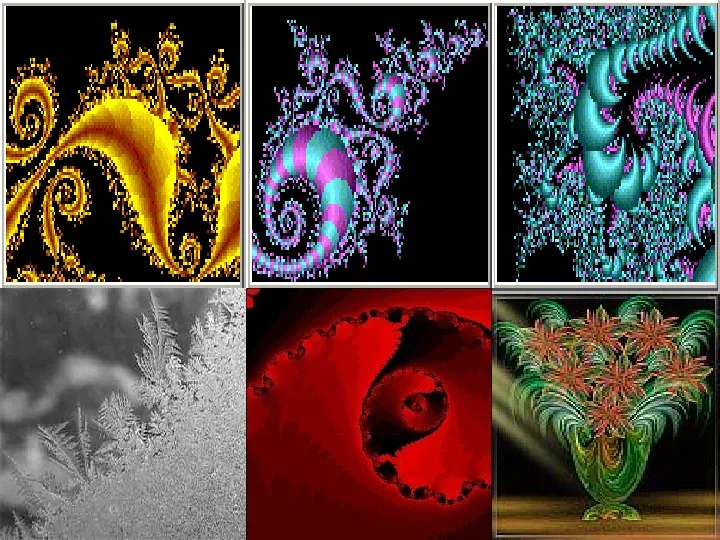
Oto przykłady niektórych fraktali

Slide 13

Niektóre, proste przykłady fraktali można pokazać uczniom gimnazjum (a może i nawet już szkoły podstawowej). Wystarczy wykonanie paru rysunków. Narysuj kwadrat (o boku np. 4 cm). Następnie na każdym boku zbuduj kwadrat o długości boku dwa razy mniejszej, tak jak na rysunku poniżej (rysunek po lewej stronie). Powtarzaj to budowanie tak długo, jak będzie to możliwe. Kwadraty rysowane w tym samym kroku pomaluj tym samym kolorem. Co przedstawia tabelka? Spróbuj wypełniać ją dalej. Nr wzoru (kroku) Kwadrat Trójkąt 1 2 3 4 ... 120 422 1624 6426 ... 130 331 932 2733 ...

Slide 14

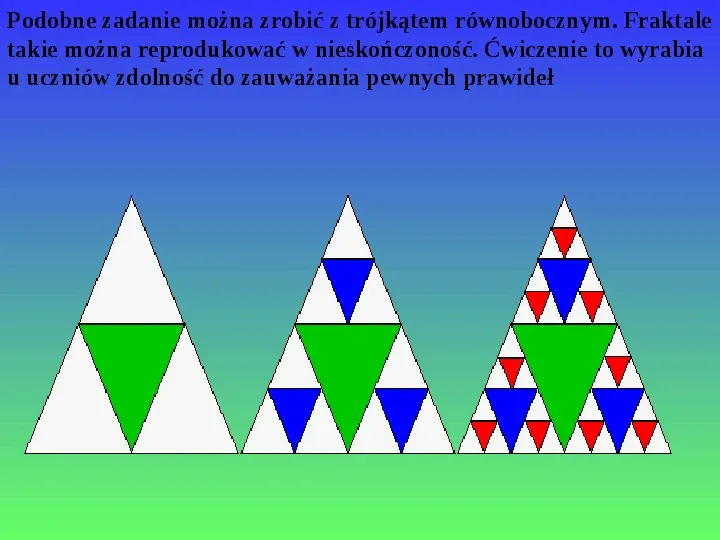
Podobne zadanie można zrobić z trójkątem równobocznym. Fraktale takie można reprodukować w nieskończoność. Ćwiczenie to wyrabia u uczniów zdolność do zauważania pewnych prawideł

Slide 15

Fraktale można też tworzyć jak na rysunkach poniżej, wchodząc do wnętrza trójkąta lub kwadratu.

Slide 16

Najstarsze fraktale Fraktale ,które wymyślili matematycy na początku XX-wieku. To dziwne i ciekawe zarazem zbiory które dały początek nowej geometrii zwanej geometrią fraktalną, która pozwala modelować wiele obiektów i zjawisk występujących w przyrodzie i nie tylko...

Slide 17

Oto niektóre własności fraktali . Fraktal to zbiór o skomplikowanej budowie. Niezależnie od tego jak mały jego fragment będziemy oglądać - będzie on równie skomplikowany jak całość. Wiele fraktali kryje w sobie zadziwiającą tajemnicę jaką jest ich nieskończone samopodobieństwo. Oznacza to, że dowolnie mały jego kawałek, odpowiednio powiększony, przypomina do złudzenia cały zbiór lub jego znaczną część. Jednocześnie fraktale mają prosty opis i często są otrzymywane przez powtarzanie nieskończenie wiele razy tej samej operacji. Jeśli przeczytacie opisy konstrukcji fraktali, które widać na ekranie, zrozumiecie co chcieliśmy powiedzieć. -

Slide 18

FRAKTALE WYSTĘPUJŁCE W PRZYRODZIE Z uwagi na fakt, iż materia zbudowana jest z atomów, nie można mówił o obiektach zawierających nieskończoną liczbę szczegółów w głąb. Doszukując się fraktali w przyrodzie, mamy na myśli obiekty, które wykazują cechę samopodobieństwa na kilku poziomach. Najciekawszym przykładem są tutaj chmury; jak wykazały badania, po ich wyglądzie nie można powiedzieć w jakiej odległości od nich znajdujemy się jako obserwatorzy. Fraktalami występującymi w przyrodzie są na przykład: układ krwionośny (naczynia włosowate), płuca, kalafior, paprotka, drzewa, krzewy, lód i jego kryształy, skały, cegła, rdza, osadzające się złoto, kształt ropy wlanej do wody

Slide 19

Fraktale z naszej kolekcji to przykłady zbiorów o zdumiewających, trudnych do wyobrażenia własnościach, które wręcz przeczą naszej intuicji. Popatrzcie na brzeg płatka śniegu. Chyba każdy z Was powie o nim, że jest krzywą. Czy powiedzielibyście to samo o dywanie Sierpińskiego? Choć brzmi to może absurdalnie, dywan jest także krzywą ale o bardzo skomplikowanej budowie. Opisywane fraktale powstały na początku XX wieku w wyniku zmagań matematyków z definicją wymiaru i krzywej. Zbiory te kryją w sobie

Slide 20

Fraktale trójwymiarowe

Slide 21

Istnieją również fraktale trójwymiarowe. Najsłynniejszym przykładem takiej struktury jest opisana powyżej kostka Mengera. Istnieje również trójwymiarowo odpowiednik trójkąta Siepińskiego. Dziesięć lat po powstaniu dywanu Sierpińskiego, Karl Menger wpadł na pomysł stworzenia trójwymiarowego odpowiednika tej figury. Sposób konstrukcji jest całkowicie analogiczny, po prostu odnosimy go do sześcianu. Bryła ta jest uniwersalnym zbiorem dla wszystkich krzywych Multifraktal jest to obiekt, który w różnych swoich częściach ma różne wymiary samopodobieństwa.(def.Federa)

Slide 22

Literatura polskojęzyczna na temat fraktalnej kompresji obrazów Wl. Skarbek Metody reprezentacji obrazów cyfrowych , Akademicka Oficyna Wydawnicza PLJ, Warszawa 1993

Slide 23

Literatura angielska (Do maja 1994 obejmowała ponad 100 pozycji oto najważniejsze:) - Barnsley M., Hurd L. P. Fractal Image Compression, AK Peters. Ltd, Wellesley 1993 -- Beamont J. M. Image data compression using fractal techniques, BT technology Journal 9(4), 93-108 - Fisher Y. Fractal Image Compression, SIGGRAPH92 Course Notes -Frigaard C., Gade J., Hemmingsen T. T., Sand T. Image Compression Based on a Fractal Theory, Institute for Electronic Systems, Aalborg University, Denmark, 1994 --Jacquin A. E. Fractal Image Coding: A Review, Proceedings of the IEEE october 1993, Vol. 81 No. 10. -- Peitgen H.-O., Jurgens H., Saupe D. Chaos and fractals, Springer-Verlag, New York 1992 (chodzi tu o dodatek, napisany przez Y. Fishera) -- Skarbek Wl. Banach constructor and image compression, Instytut Podstaw Informatyki PAN, Warszawa 1994 ---- K. Mazur Tablice matematyczne, Wydawnictwo Adamantan, Warszawa 1999 - M. Tempczyk Teoria chaosu dla odważnych, Wydawnictwo Naukowe PWN, Warszawa 2002 - H. G. Schuster Chaos deterministyczny. Wprowadzenie, Wydawnictwo Naukowe PWN, Warszawa 1993

Slide 24

THE END