Złudzenia optyczne

Zobacz slidy

Treść prezentacji

Slide 2

Ostrzeżenie!!! Jeśli oglądniecie tą prezentację to przestaniecie wierzyć własnym oczom. Zobaczycie tylko wydaje wam się, że widzicie to, co widzicie. Wkroczycie w świat linii, które przecinają się, choć są równoległe, odcinków krótszych i dłuższych, ale równiej długości, albo wcale nie żartuję schodów, które zaczynają się tam, gdzie się kończą. Uff, byle nie zwariować... Czy wyrażasz zgodę, aby przejść do następnego slajdu? Tak Nie

Slide 3

Złudzenie Ebbinghausa Oto złudzenie typu kontrastowego opisane przez Ebbinghausa w 1902 roku. Koło otoczone mniejszymi kołami wydaje się sporo większe niż identyczne koło otoczone kołami większymi od siebie. Podobny efekt można zaobserwować w przypadku kwadratów.

Slide 4

Złudzenie Ficka Linia pionowa i pozioma mają tę sama długość, chociaż nie wydają się równe. Linie wydają się równe, choć pionowa jest o jedną trzecią krótsza niż pozioma. W 1851 roku Fick zauważył, że linie pionowe wydają się nam dłuższe od linii poziomych o tej samej (obiektywnie) długości. Okazuje się, że w niektórych przypadkach różnica w postrzeganej długości dwóch identycznych odcinków może dochodzić nawet do 30 procent! Zaobserwowano, że intensywność zjawiska nieco maleje, jeśli patrzymy tylko jednym okiem.

Slide 5

Złudzenie Jastrowa Spójrzcie na dwa poniższe kontury. Wydaje się niemożliwe, aby były identyczne! Przecież dolny jest najwyraźniej większy?! Jeśli jednak odrysujecie jeden z nich i położycie na drugi, to zobaczycie, że pasują do siebie idealnie! To niezwykle silne złudzenie odkrył Jastrow, około 1890 roku. Jeśli to też przykład złudzenia opartego na kontraście: krótsza linia górnego konturu kontrastuje z dłuższą linią dolnego.

Slide 6

Złudzenie Zöllnera Trochę nietypowe przedstawienie złudzenia Zöllnera. Linie pomiędzy okręgami mogą wydać się pofalowane. Linie równoległe wydają się lekko pochylone nawzajem siebie. Takie wrażenie wywołują różnie pochylone kreski na tych odcinkach.

Slide 7

Złudzenie Poggendorfa Jest to w zasadzie podstawowy element składowy złudzenia Zőllnera. Dwa fragmenty linii widocznej po obu stronach prostokąta są swoim wzajemnym przedłużeniem, choć wydaje się, że są przesunięte względem siebie.

Slide 8

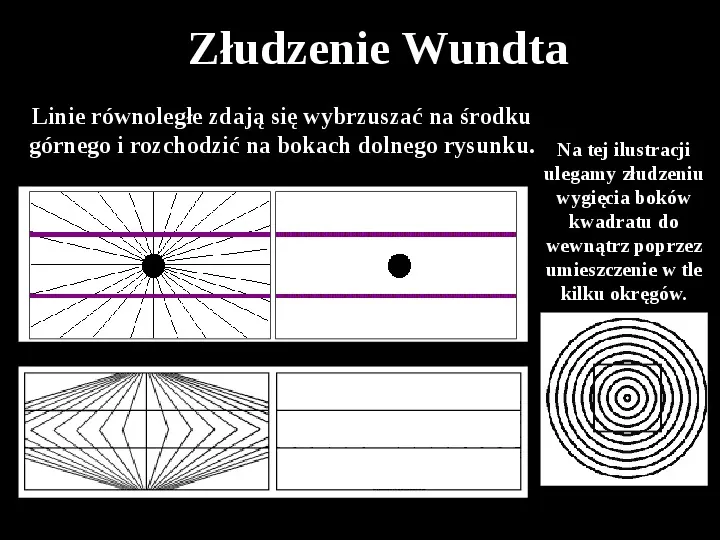
Złudzenie Wundta Linie równoległe zdają się wybrzuszać na środku górnego i rozchodzić na bokach dolnego rysunku. Na tej ilustracji ulegamy złudzeniu wygięcia boków kwadratu do wewnątrz poprzez umieszczenie w tle kilku okręgów.

Slide 9

Złudzenie Ponza Zwane jest także czasem złudzeniem torów kolejowych, a opublikował je włoski psycholog Mario Ponzo w 1913 roku. Górny odcinek, bliżej wierzchołka, wydaje nam się dłuższy. I w tym przypadku nie mam jednego, całkowicie przekonującego wyjaśnienia iluzji. Niewątpliwie rozwiązanie zagadki powinno mieć coś wspólnego z odczuciem perspektywy.

Slide 10

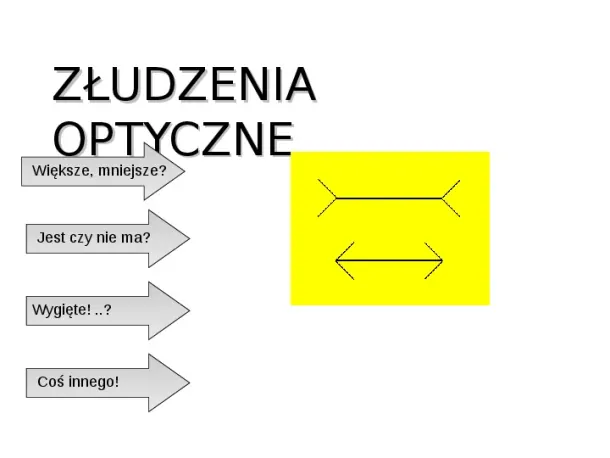
Złudzenie Müllera - Lyera Który odcinek jest dłuższy? Trudno uwierzyć, że są identyczne! Iluzję tę opublikował Franz Müller Lyer w 1889 roku. Szybko zaproponowano kilka (niestety nieprzekonujących) wyjaśnień efektu.

Slide 11

Nie istniejące obiekty Czy można zobaczyć coś co nie istnieje? Jasne! I to nie tylko zobaczyć można to również narysować. Najsłynniejszym przykładem jest niemożliwy trójkąt Rogera Penrosea. W zależności od spojrzenia na ilustrację (góra lub dół) dostrzeżemy, że raz drzwi otwarte są na zewnątrz, a raz do środka Jedna z niesamowitych brył autorstwa Oscara Reuterswarda

Slide 12

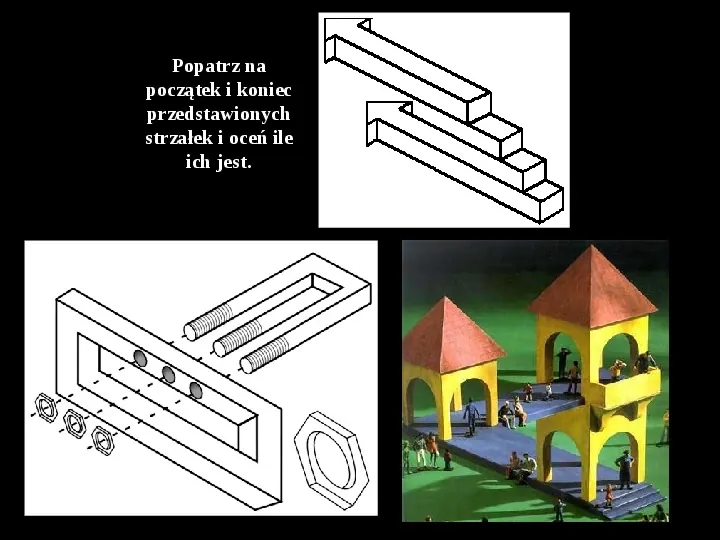
Popatrz na początek i koniec przedstawionych strzałek i oceń ile ich jest.

Slide 13

Nie istniejące kontury Powyżej: przykład wyraźnych czarnych konturów widocznych na czarnym tle! Złudzenie to wymyślił włoski psycholog Gaetano Kanizsa.

Slide 14

Schody Schrödera

Slide 15

Po chwili intensywnego wpatrywania się w powyższy rysunek widać sześć sześcianów ustawionych w piramidę. Czy, aby na pewno? A może to jest siedem sześcianów?

Slide 16

Złudzenie Münstenberga Linie oddzielające poszczególne pionowe rzędy tej ciekawej mozaiki wydają się pokrzywione. Są jednak proste, a nawet wzajemnie równoległe. Złudzenie pochodzi z XIX wieku. Czy uwierzysz, że liny na prawej ilustracji wiszą pionowo, są proste i równoległe wobec siebie? Efekt ich odgięcia powodują czarne elementy umieszczone na linach.

Slide 17

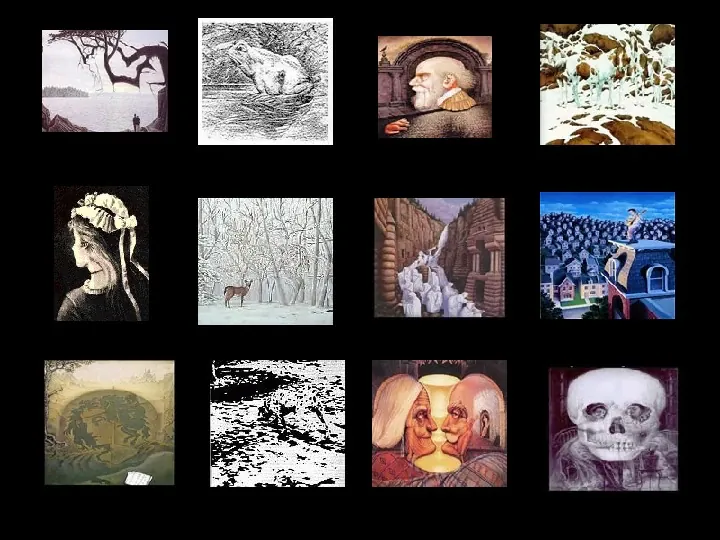
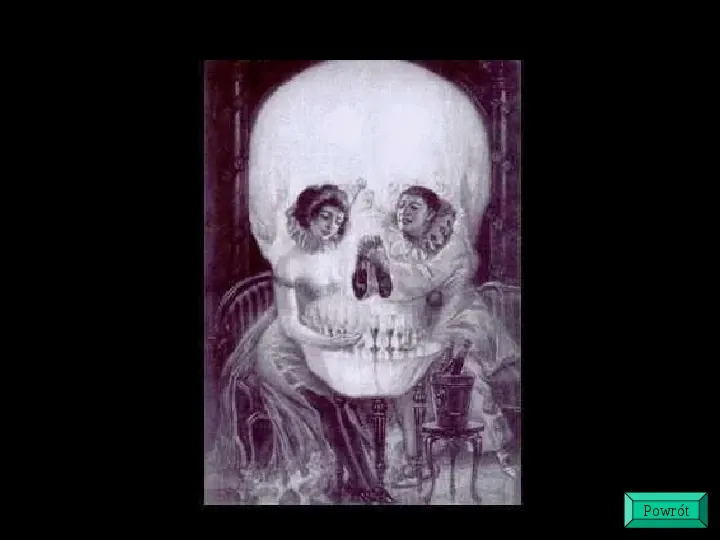
Dwa w jednym Oto obiekty nie jedno znaczne. Możemy wprawdzie z łatwością przestawiać się miedzy dwiema wersjami obrazka, ale nie możemy zobaczyć obu naraz.

Slide 21

Kielich Rubina Bardzo ważną umiejętnością jest wyodrębnienie obiektu z tła. Jest to zwykle tym łatwiejsze, im wyraźniejsze są granice obiektu. Jednak podział na tło i obiekt nie zawsze jest rzeczą prostą. Popatrzcie na kielich Rubina. Zarówno profile twarzy, jak i kielich ze środka rysunku z równą natarczywością domagają się naszej uwagi.

Slide 22

Trójwymiarowe: Patrząc na ilustracje po raz pierwszy można stwierdzić, że postać w głębi jest większa od postaci znajdującej się bliżej oglądającego. W rzeczywistości są one sobie równe. Przy ocenie wielkości zrobiliśmy błąd, ponieważ wzięliśmy pod uwagę perspektywę i tło ilustracji. Pokój Amesa o dziwnym kształcie i kątach stwarza perspektywę, co w zwykłym pokoju. W rezultacie powstaje błędne wrażenie, że dzieci są w tej samej odległości od osoby patrzącej. Mózg nie poprawia wzrostu dziewczynki, zatem postrzegamy ją jako niższą od chłopca.

Slide 23

Dziwne napisy Napis stworzony przez amerykańskiego artystę. Po obróceniu o 180 stopni przedstawia on to samo, co przed obrotem. TrueFalse - praca jest przykładem na to, jak artysta zręcznie umieszczał w jednym słowie drugie o przeciwnym znaczeniu.

Slide 26

Ruszające się obrazki

Slide 29

Wpatruj się w środek przedstawionej ilustracji i oddalaj po czym przybliżaj wzrok. Okręgi będą wydawały się obracać. Na pierwszy rzut oka wydaje się, że na ilustracji przedstawiona jest spirala. W rzeczywistości jest to tylko zbiór okręgów o różnych promieniach.

Slide 30

Wpatruj się w czarną kropkę na środku ilustracji przez około 30 sek. Po chwili szare pole wokół kropki zacznie zanikać, aż do momentu, w którym będzie kompletnie niewidoczne. Wariacja ilustracji znajdującej się wcześniej. Poświata znika do granicy poprzecinanej obręczy.

Slide 31

Inne: Grafika autorstwa Sandro del Prete pt. Columns. Patrząc na górę ilustracji widzimy dwie kwadratowe kolumny, patrząc na dół, trzy okrągłe. Czy uwierzysz, że odcinek AB jest równy, co do długości odcinkowi BC?

Slide 32

Ile tu jest kolorów? Są tylko trzy: biały, różowy i zielony. Dlaczego więc widać więcej? To efekt kontrastu: ciemniejsze kolory zestawione razem wydają się intensywniejsze. Czy uwierzysz, że szary poziomy pasek jest w rzeczywistości jednolicie szary, a efekt zmiany jego barwy powoduje kontrast z tłem. Na ilustracji widzimy tzw. Siatkę Hermana. Na przecięciu szarych linii można dostrzec szare - czarne plamy, których w rzeczywistości nie ma.

Slide 33

5

Slide 34

Powrót

Slide 35

Powrót

Slide 36

Powrót

Slide 37

Powrót

Slide 38

Powrót

Slide 39

Powrót

Slide 40

Powrót

Slide 41

Powrót

Slide 42

Powrót

Slide 43

Powrót

Slide 44

Powrót

Slide 45

Powrót

Slide 46

Powrót

Slide 47

Powrót

Slide 48

Powrót

Slide 49

Powrót

Slide 50

Powrót

Slide 51

Powrót

Slide 52

Powrót

Slide 53

Powrót

Slide 54

Powrót

Slide 55

Powrót

Slide 56

Powrót

Slide 57

Powrót

Slide 58

Powrót