Podstawy krystalografii

Zobacz slidy

Treść prezentacji

Slide 1

Podstawy krystalografii Michał Sobczak

Slide 2

Sieć Baza Struktura krystaliczna Sieć regularny układ punktów zdefiniowany przez podstawowe wektory translacji sieci. Abstrakcja matematyczna. Baza atomowa atomy lub cząsteczki przypisane do węzłów sieci.

Slide 3

Wektory translacji sieci Podstawowe wektory translacji a1 , a 2 , a3 definiują sieć w taki sposób, żeułożenie atomów wygląda tak samo z punku z punktu r. r jak i r r u1 a1 u 2 a 2 u 3 a3 T Gdzie u1 , u 2 , u 3 są dowolnymi liczbami całkowitymi. T jest wektorem translacji sieci. Mówimy, że kryształ jest niezmienniczy ze względu na translację.

Slide 4

Komórka elementarna Najmniejszy obszar sieci przestrzennej wyodrębniony przez sześć płaszczyzn parami równoległych, mający kształt równoległościanu. Równoległościan zdefiniowany jest przez podstawowe wektory translacji.

Slide 5

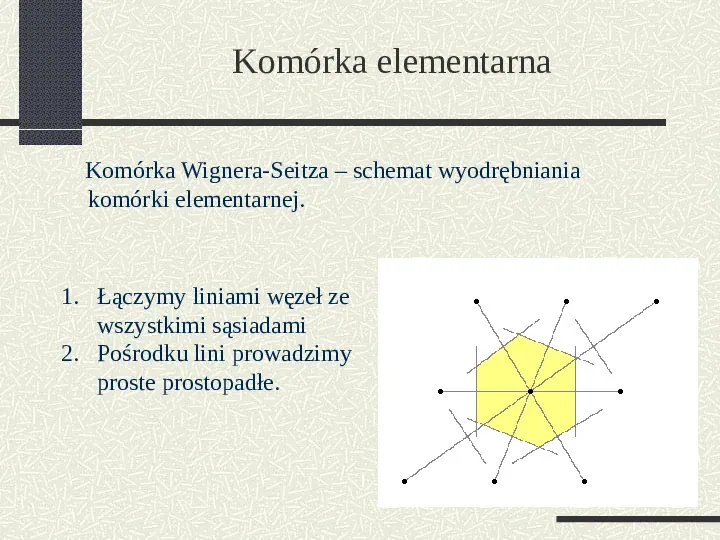
Komórka elementarna Komórka Wignera-Seitza schemat wyodrębniania komórki elementarnej. 1. Łączymy liniami węzeł ze wszystkimi sąsiadami 2. Pośrodku lini prowadzimy proste prostopadłe.

Slide 6

Sieci Bravais Złożenie 7 systemów krystalograficznych oraz 4 sposobów centrowania teoretycznie daje 28 sieci Bravais, w rzeczywistości występuje 14. Układ Centrowań Krawędzie i kąty Trójskośny 1 a b c, 90º Jednoskośny 2 a b c, 90º Rombowy 4 a b c, 90º Tetragonalny 2 a b c, 90º Regularny 3 a b c, 90º Romboedryczny (trygonalny) 1 a b c, 90º, 120º a b c, 90º Heksagonalny 1 a b c, 90º, 120º

Slide 7

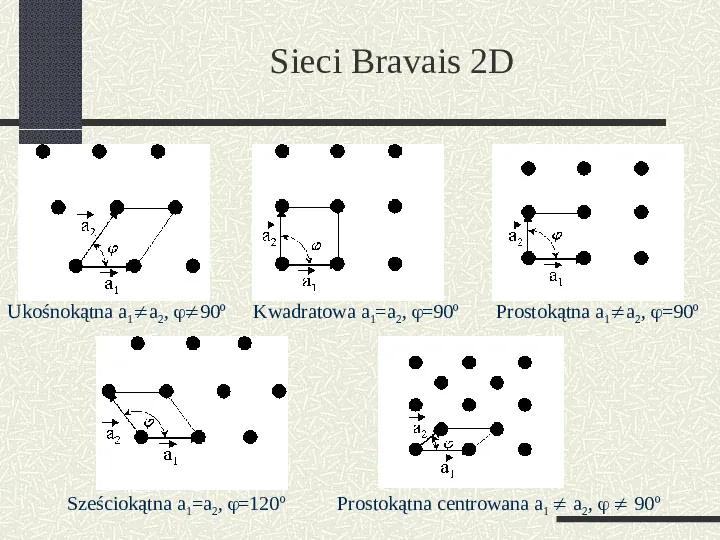
Sieci Bravais 2D Ukośnokątna a1a2, 90º Kwadratowa a1a2, 90º Sześciokątna a1a2, 120º Prostokątna a1a2, 90º Prostokątna centrowana a1 a2, 90º

Slide 8

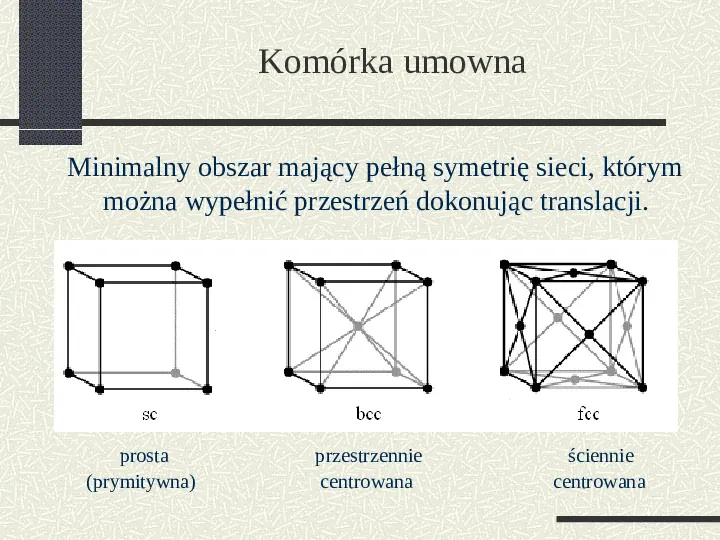
Komórka umowna Minimalny obszar mający pełną symetrię sieci, którym można wypełnić przestrzeń dokonując translacji. prosta (prymitywna) przestrzennie centrowana ściennie centrowana

Slide 9

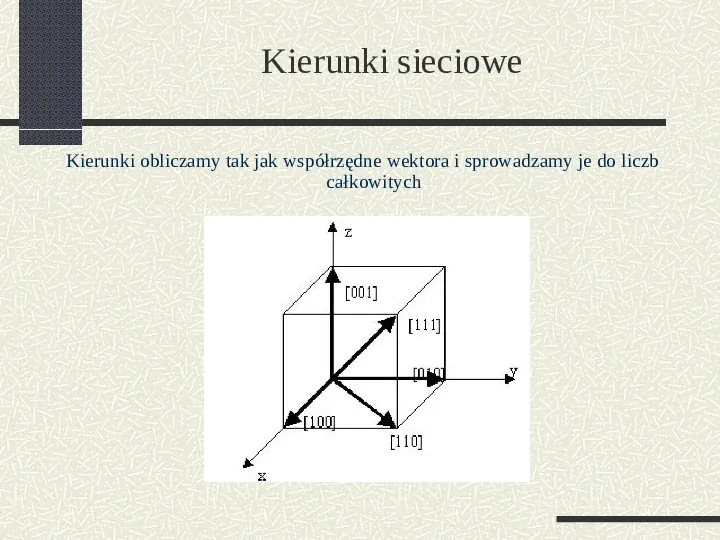
Kierunki sieciowe Kierunki obliczamy tak jak współrzędne wektora i sprowadzamy je do liczb całkowitych

Slide 10

Płaszczyzny sieciowe Płaszczyzna sieciowa płaszczyzna na której leżą co najmniej 3 węzły sieci nie leżące na jednej prostej. W związku z tym płaszczyzn w krysztale jest nieskończenie wiele. Płaszczyzny równoległe tworzą rodzinę identycznych płaszczyzn sieciowych.

Slide 11

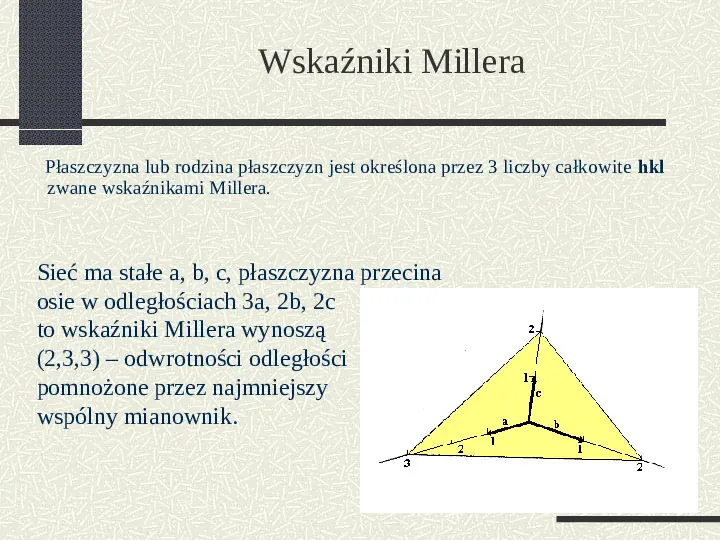
Wskaźniki Millera Płaszczyzna lub rodzina płaszczyzn jest określona przez 3 liczby całkowite hkl zwane wskaźnikami Millera. Sieć ma stałe a, b, c, płaszczyzna przecina osie w odległościach 3a, 2b, 2c to wskaźniki Millera wynoszą (2,3,3) odwrotności odległości pomnożone przez najmniejszy wspólny mianownik.

Slide 12

Sieć odwrotna a a3 podstawowymi wektorami siecikrystalicznej, Jeżeli to podstawowe 1 , a 2 ,, są wektory sieci odwrotnej ,są zdefiniowane: b1 , b2 , b3 a 2 a 3 b1 2π a 1 a 2 a 3 a 3 a 1 b 2 2π a 1 a 2 a 3 a 1 a 2 b 3 2π a 1 a 2 a 3

Slide 13

Sieć odwrotna 2D a Jeżeli to podstawowe 1 ,,asą 2 podstawowymi wektorami sieci dwuwymiarowej, wektory sieci odwrotnej ,są zdefiniowane: b1 ,b2 a 2 n b1 2π a 1 a 2 n n a 1 b 2 2π a 1 a 2 n Gdzie, n jest jednostkowym wektorem prostopadłym do powierzchni.

Slide 14

Strefa Brillouina W sieci odwrotnej podobnie jak w sieci prostej, definiuje się komórkę elementarną. Komórkę elementarną sieci odwrotnej nazywamy pierwsza strefą Brillouina. Konstrukcja pierwszej strefy jest identyczna z konstrukcją komórki Wignera-Seitza sieci prostej.

Slide 15

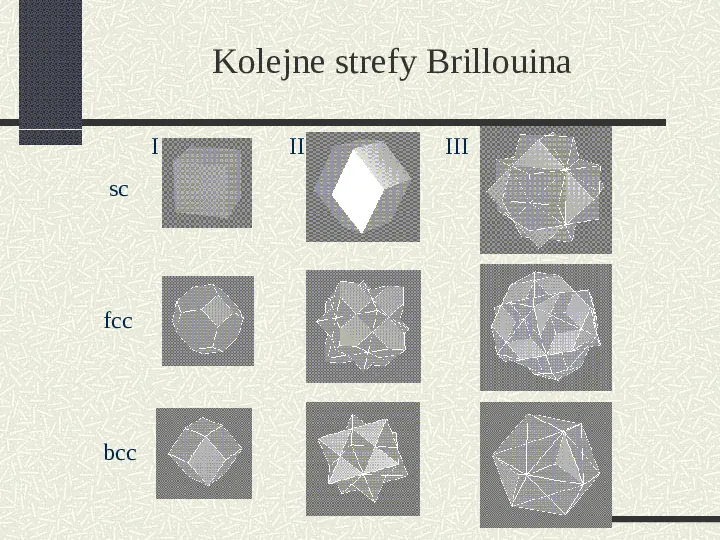
Kolejne strefy Brillouina I sc fcc bcc II III

Slide 16

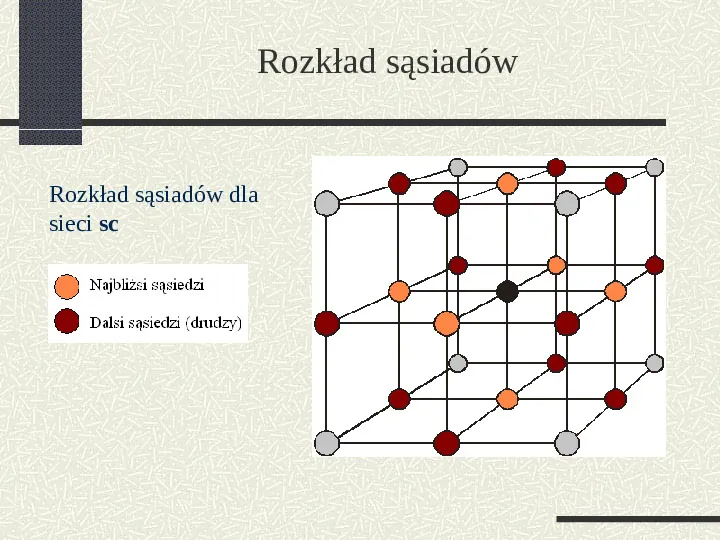
Rozkład sąsiadów Rozkład sąsiadów dla sieci sc

Slide 17

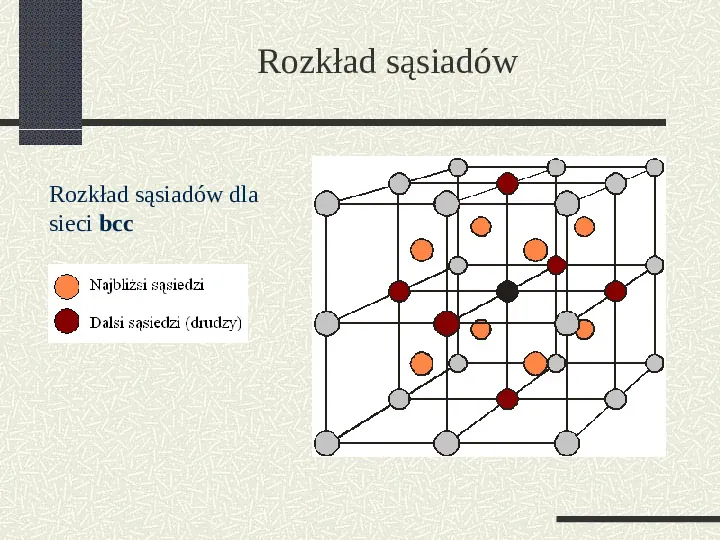
Rozkład sąsiadów Rozkład sąsiadów dla sieci bcc

Slide 18

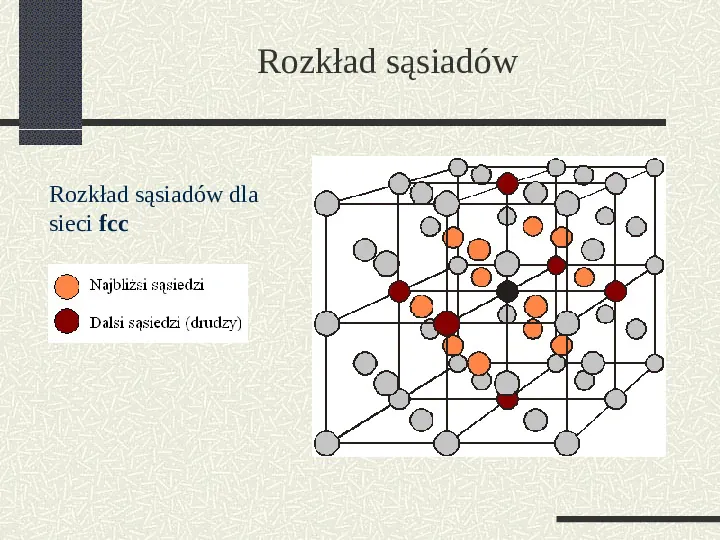
Rozkład sąsiadów Rozkład sąsiadów dla sieci fcc

Slide 19

Definicja sumy strukturalnej Suma strukturalna jest to suma po odpowiednich sąsiadach leżących w danej płaszczyźnie sieciowej, określona jest wzorem: N n gdzie: k l exp ik j l j k - wektor falowy równoległy do płaszczyzny o określonej orientacji powierzchniowej, l j - wektor położenia rzutu odpowiedniego sąsiada leżącego w płaszczyźnie lln wybranego węzła z płaszczyzny l, indeks górny N dotyczy drugich sąsiadów.

Slide 20

Koniec Dziękuję za uwagę.