Metoda kartogramów

Zobacz slidy

Treść prezentacji

Slide 1

Metoda kartogramów

Slide 2

Definicja Metoda służy do przedstawiania średniej intensywności zjawiska w granicach określonych pól odniesienia. Wartości obliczane są dla określonych jednostek odniesienia względny charakter danych (relacja dwóch zjawisk zmiennej i wartości stałej której wyrazem jest ułamek o stałym mianowniku).

Slide 3

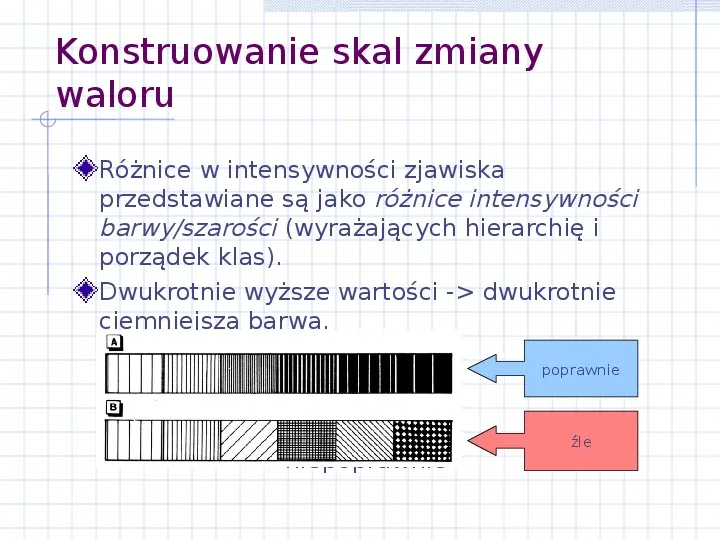
Konstruowanie skal zmiany waloru Różnice w intensywności zjawiska przedstawiane są jako różnice intensywności barwyszarości (wyrażających hierarchię i porządek klas). Dwukrotnie wyższe wartości - dwukrotnie ciemniejsza barwa. poprawnie niepoprawnie poprawnie źle

Slide 4

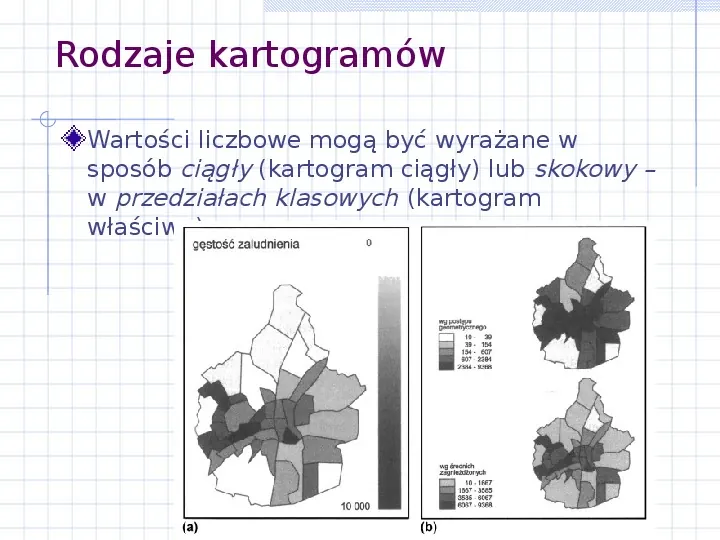
Rodzaje kartogramów Wartości liczbowe mogą być wyrażane w sposób ciągły (kartogram ciągły) lub skokowy w przedziałach klasowych (kartogram właściwy).

Slide 5

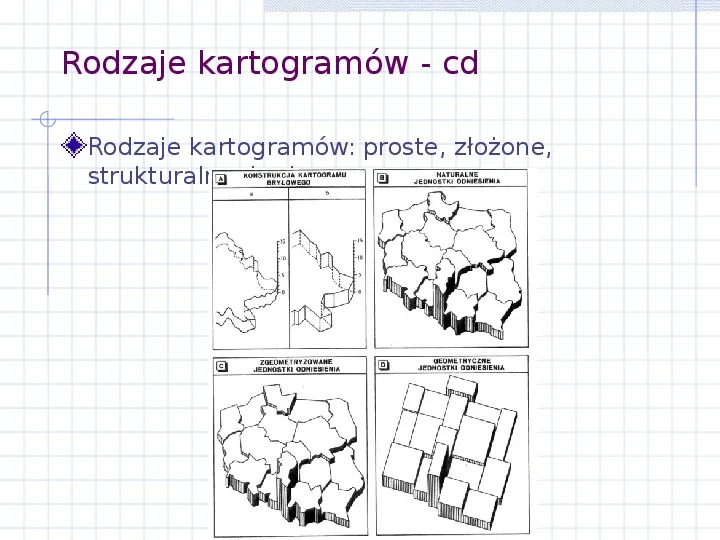
Rodzaje kartogramów - cd Rodzaje kartogramów: proste, złożone, strukturalne, bryłowe.

Slide 6

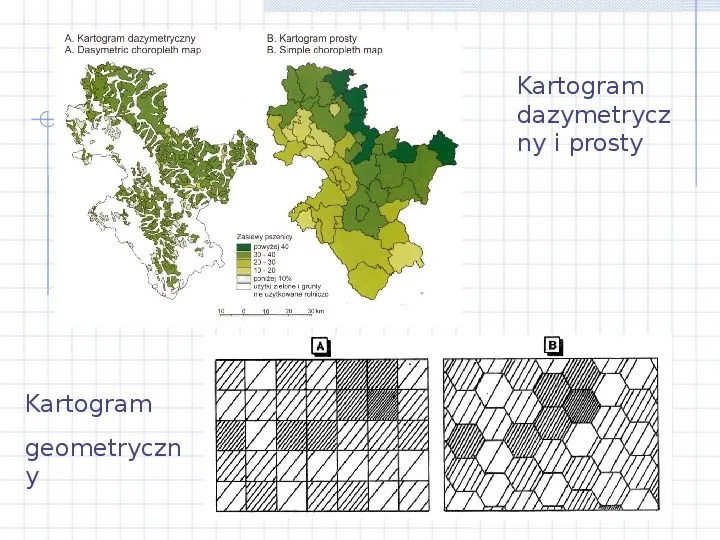
Rodzaje kartogramów - cd Uwzględniając charakter rozmieszczenia zjawiska można dokonać pewnych zmian, np. zmienić granice jednostek odniesienia: Kartogram geometryczny jednostki odniesienia figury geometryczne Kartogram dazymetryczny jednostki odniesienia dostosowane do rzeczywistego rozmieszczenia zjawiska Zastosowanie tych rodzajów kartogramów daje znacznie lepszy obraz gęstości zjawiska.

Slide 7

Kartogram dazymetrycz ny i prosty Kartogram geometryczn y

Slide 8

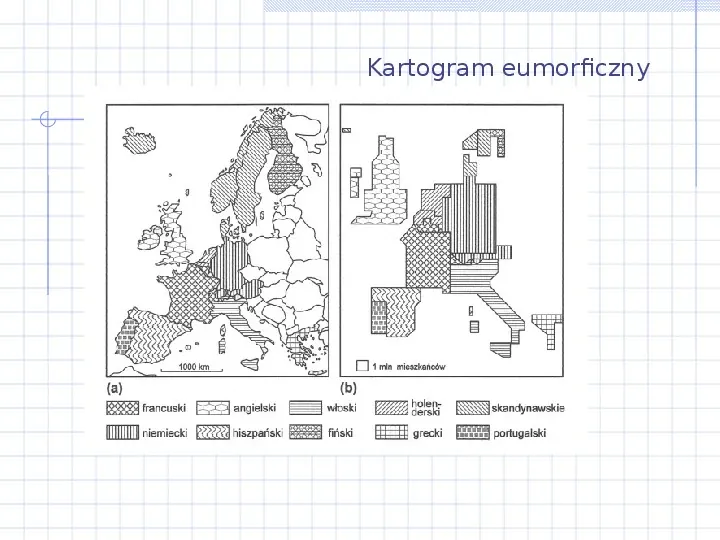
Kartogram eumorficzny Kartogram może wywoływać fałszywe wrażenie zróżnicowania wartości, które nie zostały odniesione do powierzchni. W celu uniknięcie tego efektu stosuje się korektę obrazu poprzez ważenie wartości lub zmianę jednostek odniesienia. Inne rozwiązanie polega na zastosowaniu kartogramu eumorficznego, który polega na wykorzystaniu wielkości jednostek odniesienia jako nośnika informacji i określenia ich wielkości proporcjonalnie do wartości

Slide 9

Kartogram eumorficzny

Slide 10

Rodzaje ujęcia tematu Mapy gęstości przedstawiają stosunek wartości do powierzchni. Mapy wskaźników przedstawiają stosunek dwóch wartości (zmiennej i stałej) do siebie, np: Procentowe ujęcie zjawiska, np. procent bezrobotnych udział procentowy zmienna x 100 całość zbiorowości) Natężenie zjawiska, np. średni dochód na głowę ludności natężenie zmienna element odniesienia Odchylenie od średniej, np. od średniego przyrostu naturalnego odchylenie od średniej zmienna średnia Odchylenie od optymalnej, np. optymalnej normy kalorycznej spożycia odchylenie od optymalnej zmienna optymalna Udział w całości, np. udział poszczególnych województw w ogólnokrajowej wartości produkcji rolnej udział w całości zmienna całość zbiorowości

Slide 11

Zasada opracowania kartogramów Wartości bezwzględne zjawiska (a) odnoszone są do innych wartości (powierzchni) (b). Otrzymane gęstościwskaźniki grupuje się w klasy (c), którym przypisuje się stopnie szarości (inną reprezentację graficzną) (d).

Slide 12

Podział na przedziały klasowe warunki Maksymalna liczba klas 5. Można ją rozszerzyć do 7 poprzez dodanie barwy. Warunkiem prawidłowego podziału na klasy jest minimalizowanie różnic wartości w obrębie klas przy jednoczesnym maksymalizowaniu różnic między klasami. Skutkuje to tym, że granice klas widoczne na mapie będą zgodne z granicami w rzeczywistości. Należy stosować metodę, która najlepiej oddaje rozkład danych oraz dobierać przedziały tak, żeby uniknąć występowania tzw. pustych przedziałów

Slide 13

Konstrukcja przedziałów klasowych Zgodnie z [1] można wyróżnić kilka najczęściej stosowanych typów przedziałów klasowych Normatywne wynikają z przyjęcia wartości granicznych uzasadnionych charakterem funkcjonalnym danego zjawiska (np. podział ludności ze względu na wiek na przedprodukcyjną, produkcyjną i poprodukcyjną) Przedziały o jednakowej rozpiętości powstają w wyniku podziału zbiorowości na jednakowe odstępy liczbowe: BX W m ax W k m in następnie wartość BX zaokrągla się. Powstać mogą w ten sposób skale: - zamknięte dokładne (końce to wartości minmax) - zamknięte zaokrąglone (wartości minmax zaokrąglone do pełnych) - otwarte jednostronnie (wartości poniżej... lub powyżej...) - dwustronnie otwarte (analogicznie jak powyżej)

Slide 14

...cd Analityczne przedziały klasowe wyznaczane w wyniku analizy szeregu liczbowego. Pomocniczo wykorzystuje się wykresy obrazujące rozkład danych, histogramy itp. (szerzej w [1]). W pozycji [2] wyróżnia się podejście graficzne oraz matematyczne, w którym zawarte są następujące metody: Przedziały równej rozpiętości - j.w. Kwantyle liczba obserwacji dzielona przez liczbę klas. Zalecana, gdy jednostki odniesienia mają podobne pow. a redaktora interesuje relacja między wartościami tych jednostek. Ciąg arytmetyczny (tu 5 klas): Wmin C 2C 3C 4C 5C Wmax gdzie C wielkość przedziału klasowego: c M A X M IN 1 2 ... k k- liczba klas

Slide 15

...cd Ciąg geometryczny: lo g M A X lo g M IN k lo g C Wartość C wykorzystuje się we wzorze: log (najwyższej wartości) C log (drugiej najwyższej wartości) log (drugiej najwyższej wartości) C log (trzeciej najwyższej wartości) itd... Ciąg harmoniczny: 1 W m ax k 1 W m in C Wartość C wykorzystuje się we wzorze: odwrotność najwyższej wartości C (odwrotność najwyższej wartości C) C ((odwrotność najwyższej wartości C) C) C itd. Odwrotności uzyskanych wartości traktuje się jako granice klas. Metoda ta pozwala uwypuklić cechy rozkładu niskich wartości w szeregu arytmetycznym.

Slide 16

...cd Średnie zagnieżdżone wpierw oblicza się średnią wszystkich wartości (S). Następnie oblicza się średnią wszystkich wartości powyżej i poniżej S uzyskując S1 i S2 i kolejno wartości średnie dla wartości poniżej i powyżej S1 i S2. Otrzymane liczby traktuje się jako granice klas. Modyfikacja metody polega na zastosowaniu odchylenia standardowego i dodawaniu bądź odejmowaniu go od średniej arytmetycznej.

Slide 17

Literatura [1] Ratajski L., Metodyka kartografii społeczno gospodarczej, Państwowe Przedsiębiorstwo Wydawnictw Kartograficznych, Warszawa Wrocław, 1989 [2] Kraak M., Ormeling F. Kartografia. Wizualizacja danych przestrzennych, Wydawnictwo Naukowe PWN, Warszawa, 1998