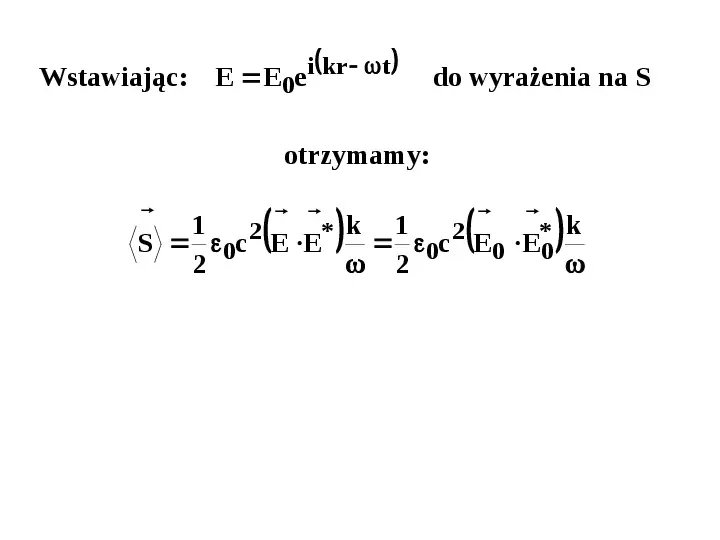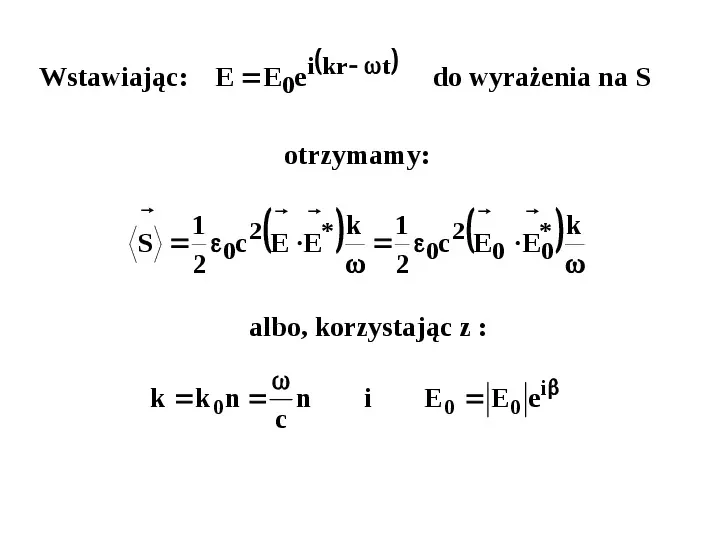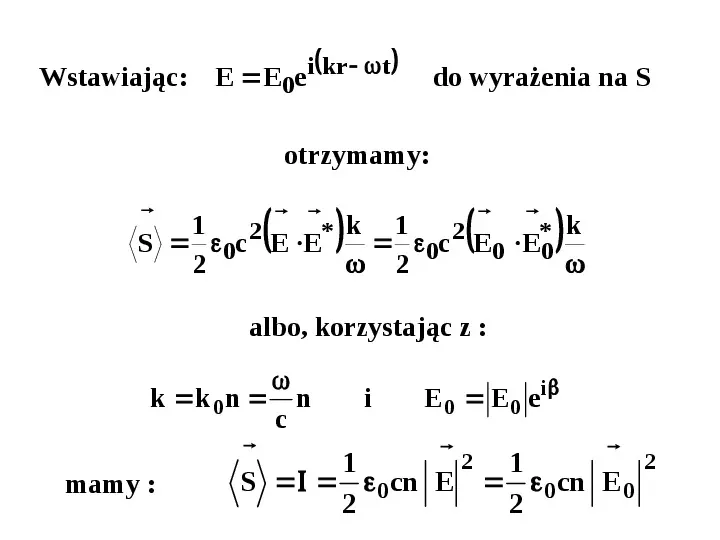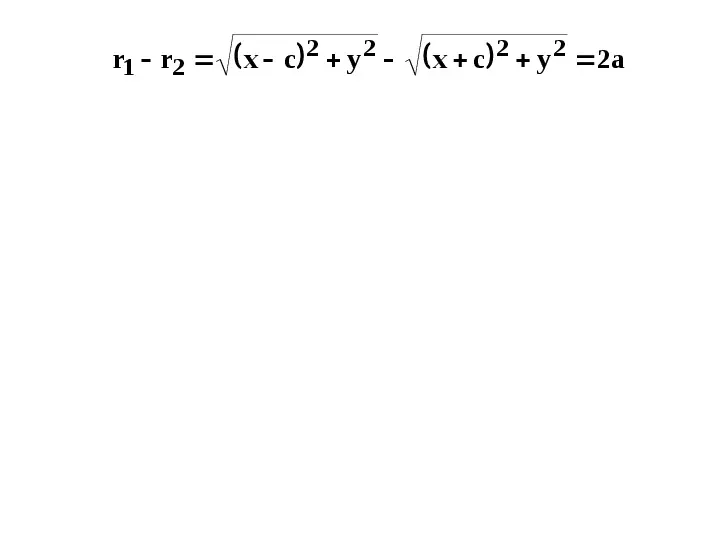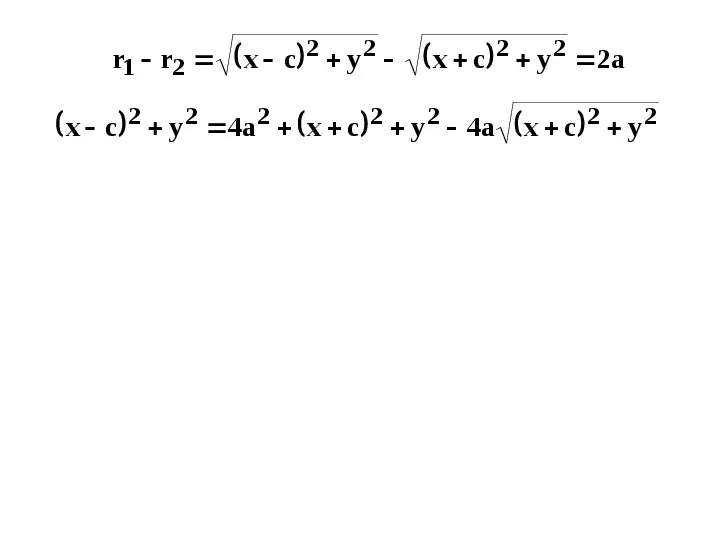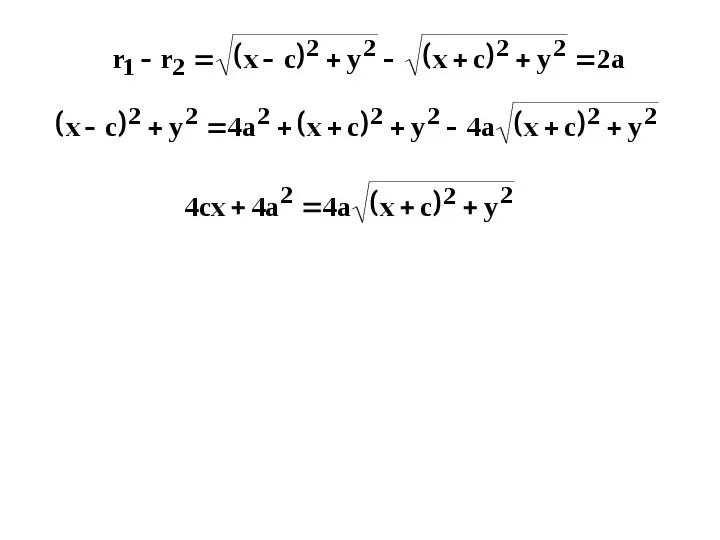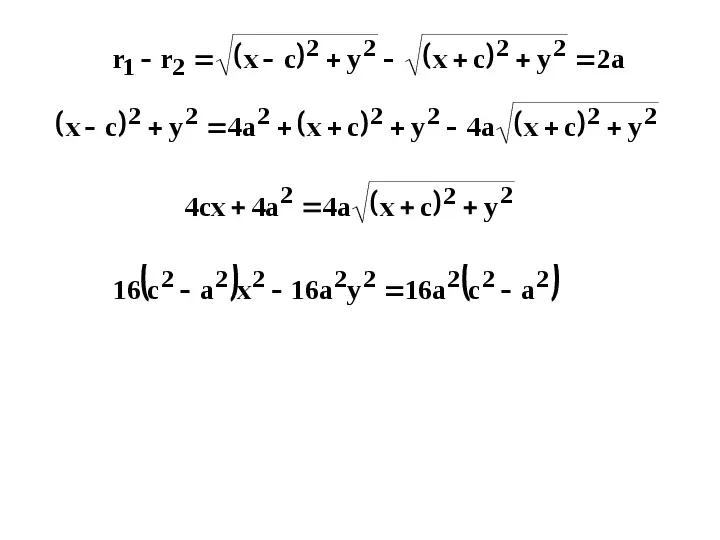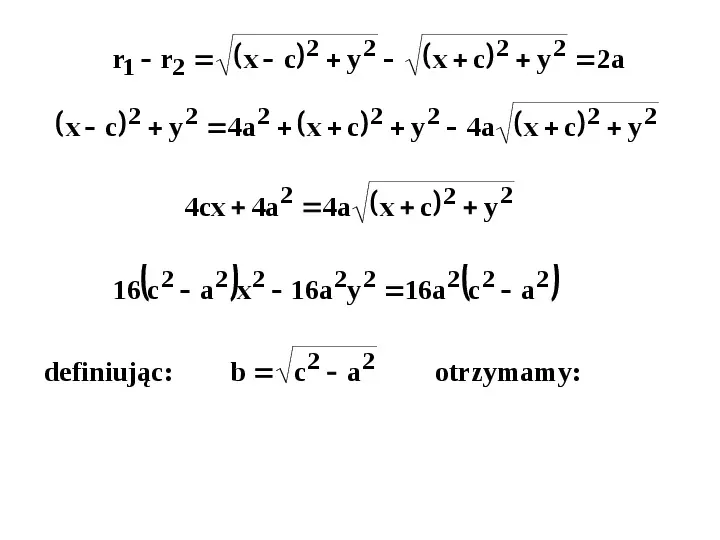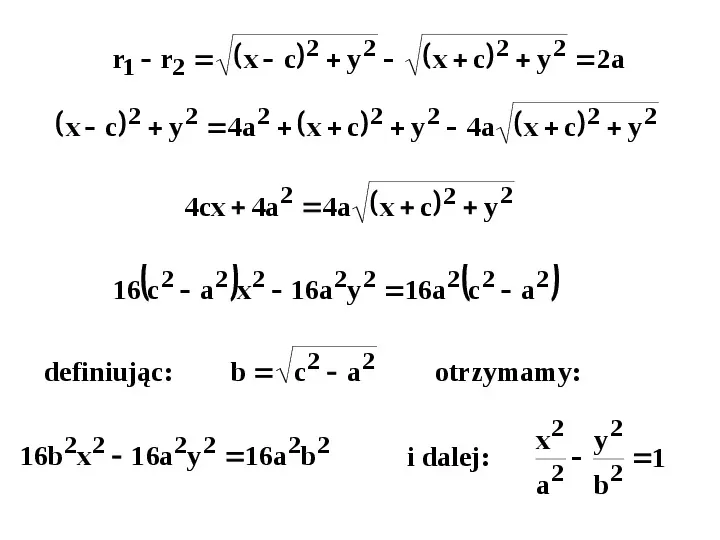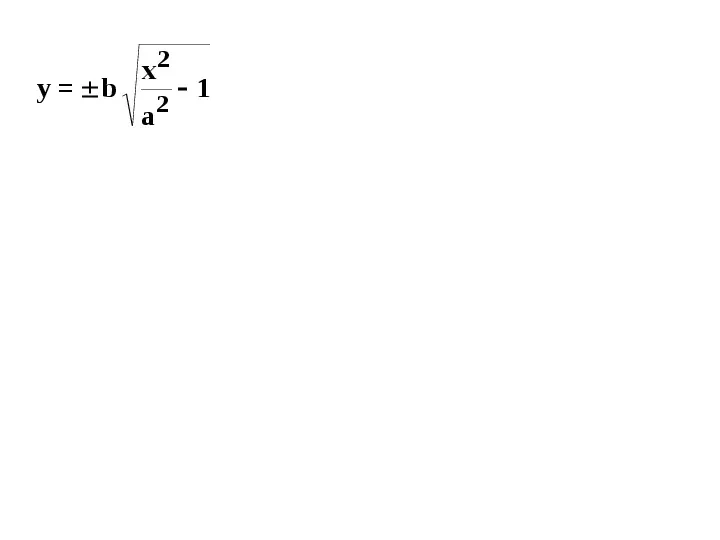Zjawiska dyfrakcji i interferencji światła spójność

Zobacz slidy

Treść prezentacji

Slide 1

WYKŁAD 11 ZJAWISKA DYFRAKCJI I INTERFERENCJI ŚWIATŁA; SPÓJNOŚĆ

Slide 2

PLAN WYKŁADU Uwagi wstępne i podstawowe pojęcia Zasada superpozycji Natężenie fali świetlnej w zapisie zespolonym Interferencja fal z dwóch spójnych źródeł punktowych PODSUMOWANIE

Slide 3

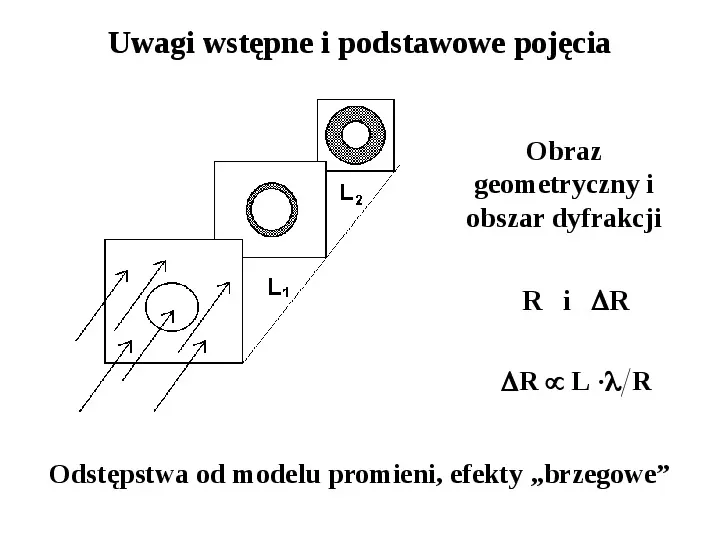
Uwagi wstępne i podstawowe pojęcia Obraz geometryczny i obszar dyfrakcji R i R R L R Odstępstwa od modelu promieni, efekty brzegowe

Slide 4

Dyfrakcja Fresnela: R L R R Dyfrakcja Fraunhofera: R L R R Niezbyt duża i wystarczająco duża odległość ekranu od otworu

Slide 5

Warunki na otrzymanie dyfrakcji: monochromatyczność spójność czasowa, stała różnica faz pomiędzy falami przechodzącymi przez ten sam punkt otworu w różnych chwilach czasu spójność przestrzenna stała różnica faz pomiędzy falami przechodzącymi przez różne punkty otworu Spójność różnych źródeł; źródło pierwotne i źródła wtórne Dyfrakcja i interferencja, nakładanie się efektów dyfrakcyjnych i interferencyjnych

Slide 6

Zasada superpozycji 2 1 2 E1 E2 2 2 c t 2 1 2 2 1 2 E1 E2 2 2 2 2 c t c t Jeśli E1 i E2 są rozwiązaniami to także E1E2 jest rozwiązaniem równania falowego. Zasada ta to podstawa teorii zjawisk dyfrakcji i interferencji

Slide 7

Natężenie fali świetlnej w zapisie zespolonym Wektor Poyntinga (natężenie, czyli energia na jednostkę czasu i jednostkę powierzchni): 2 2 k E 2 2 k S 0c E B 0c E 0c E

Slide 8

Natężenie fali świetlnej w zapisie zespolonym Wektor Poyntinga (natężenie, czyli energia na jednostkę czasu i jednostkę powierzchni): 2 2 k E 2 2 k S 0c E B 0c E 0c E Znaczenie średniej w czasie. Dla fal harmonicznych:

Slide 9

Natężenie fali świetlnej w zapisie zespolonym Wektor Poyntinga (natężenie, czyli energia na jednostkę czasu i jednostkę powierzchni): 2 2 k E 2 2 k S 0c E B 0c E 0c E Znaczenie średniej w czasie. Dla fal harmonicznych: Średnia w czasie wartość E2: 2 1 E E E 2

Slide 10

Natężenie fali świetlnej w zapisie zespolonym Wektor Poyntinga (natężenie, czyli energia na jednostkę czasu i jednostkę powierzchni): 2 2 k E 2 2 k S 0c E B 0c E 0c E Znaczenie średniej w czasie. Dla fal harmonicznych: Średnia w czasie wartość E2: 1 2 2 2 E0 cos t E0 2 2 1 E E E 2 E0eit E0e it E02

Slide 11

i kr t Wstawiając: E E0e do wyrażenia na S otrzymamy: 1 2 k 1 2 k S 0c E E 0c E0 E0 2 2

Slide 12

i kr t Wstawiając: E E0e do wyrażenia na S otrzymamy: 1 2 k 1 2 k S 0c E E 0c E0 E0 2 2 albo, korzystając z : k k 0 n n c i E 0 E 0 e i

Slide 13

i kr t Wstawiając: E E0e do wyrażenia na S otrzymamy: 1 2 k 1 2 k S 0c E E 0c E0 E0 2 2 albo, korzystając z : k k 0 n n c mamy : i E 0 E 0 e i 2 1 2 1 S 0cn E 0cn E 0 2 2

Slide 14

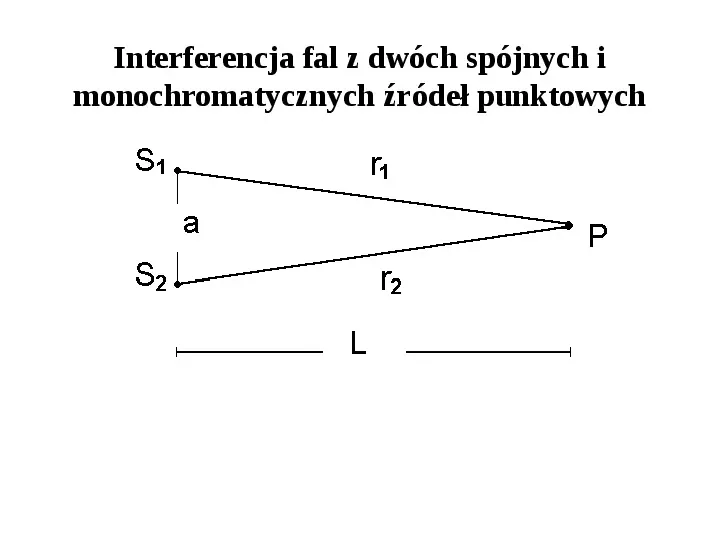
Interferencja fal z dwóch spójnych i monochromatycznych źródeł punktowych

Slide 15

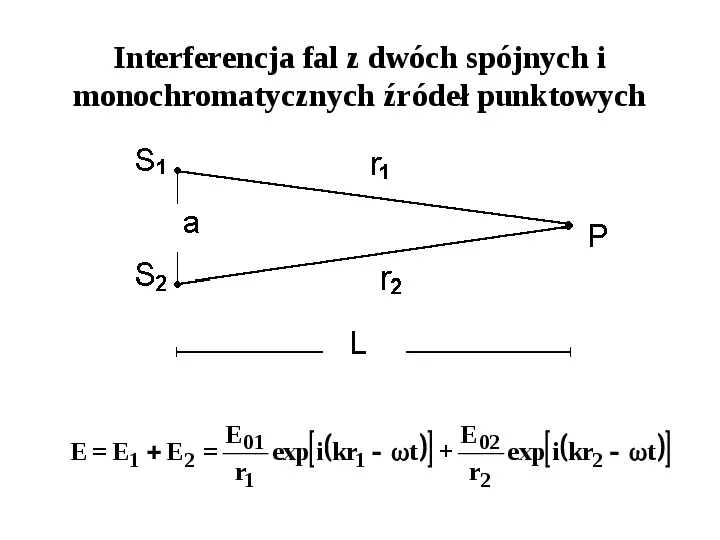
Interferencja fal z dwóch spójnych i monochromatycznych źródeł punktowych E 01 E 02 E E1 E 2 exp i kr1 t exp i kr2 t r1 r2

Slide 16

Całkowite uśrednione w czasie natężenie I(P): 1 I P 0cn E1 E2 E1 E2 2

Slide 17

Całkowite uśrednione w czasie natężenie I(P): 1 I P 0cn E1 E2 E1 E2 2 1 1 1 cn E E E E 0cn E1E1 0cn E2E2 0 1 2 2 1 2 2 2

Slide 18

Całkowite uśrednione w czasie natężenie I(P): 1 I P 0cn E1 E2 E1 E2 2 1 1 1 cn E E E E 0cn E1E1 0cn E2E2 0 1 2 2 1 2 2 2 2 2 1 E01 1 E02 0cn 0cn 2 2 2 2 r1 r2 1 E01E02 exp ik r1 r2 exp ik r2 r1 0cn 2 r1r2

Slide 19

Ostatecznie otrzymamy: gdzie: I P I1 I 2 2 I1I 2 cos 2 r1 r2 r1 r2 2 k r1 r2 2 ,

Slide 20

Ostatecznie otrzymamy: gdzie: I P I1 I 2 2 I1I 2 cos 2 r1 r2 r1 r2 2 k r1 r2 2 , Imax I1 I 2 2 I1I 2 r1 r2 m m, m 0,1,2,3... interferencja konstruktywna

Slide 21

Ostatecznie otrzymamy: gdzie: I P I1 I 2 2 I1I 2 cos 2 r1 r2 r1 r2 2 k r1 r2 2 , Imax I1 I 2 2 I1I 2 r1 r2 m interferencja konstruktywna Imin I1 I 2 2 I1I 2 r1 r2 2n 1 2 m, m 0,1,2,3... 1 2n 1 , n 0,1,2,3... 2 interferencja destruktywna

Slide 22

Przypadek jednakowych źródeł: I 2I 0 2I 0 cos 2 2I 0 1 cos 2 4I 0 cos2 zerowe natężenia w ciemnych prążkach

Slide 23

Interferencja konstruktywna: r1 r2 m, gdzie m 0, 1, 2, 3, ... geometryczna definicja hiperboli: miejsce geometryczne punktów, których bezwzględna wartość różnicy odległości od dwóch punktów (ognisk) jest stała

Slide 24

Hiperboloida jasnego prążka dla: r1 r2 m 2a, a m 2 , 1; m 8 m 8 , S1S 2 2c 10

Slide 25

r1 r2 x c 2 y 2 x c 2 y 2 2a

Slide 26

r1 r2 x c 2 y 2 x c 2 y 2 2a x c 2 y 2 4a2 x c 2 y 2 4a x c 2 y 2

Slide 27

r1 r2 x c 2 y 2 x c 2 y 2 2a x c 2 y 2 4a2 x c 2 y 2 4a x c 2 y 2 4cx 4a 2 4a x c 2 y 2

Slide 28

r1 r2 x c 2 y 2 x c 2 y 2 2a x c 2 y 2 4a2 x c 2 y 2 4a x c 2 y 2 4cx 4a 2 4a x c 2 y 2 16 c2 a 2 x 2 16a 2y 2 16a 2 c2 a 2

Slide 29

r1 r2 x c 2 y 2 x c 2 y 2 2a x c 2 y 2 4a2 x c 2 y 2 4a x c 2 y 2 4cx 4a 2 4a x c 2 y 2 16 c2 a 2 x 2 16a 2y 2 16a 2 c2 a 2 definiując: b c2 a2 otrzymamy:

Slide 30

r1 r2 x c 2 y 2 x c 2 y 2 2a x c 2 y 2 4a2 x c 2 y 2 4a x c 2 y 2 4cx 4a 2 4a x c 2 y 2 16 c2 a 2 x 2 16a 2y 2 16a 2 c2 a 2 definiując: b c2 a2 16b 2x 2 16a 2y 2 16a 2b 2 otrzymamy: i dalej: x2 a2 y2 b2 1

Slide 31

y b x2 a 2 1

Slide 32

y b x2 a 2 1 Pomijając jedynkę otrzymamy: y bx a dwie proste na płaszczyźnie, stożek w przestrzeni

Slide 33

y b x2 a 2 1 Pomijając jedynkę otrzymamy: y bx a dwie proste na płaszczyźnie, stożek w przestrzeni Na płaszczyźnie (płaskim ekranie) otrzymamy krzywe stożkowe; dla płaszczyzny równoległej do prostej na której leżą źródła, hiperbole, dla płaszczyzny prostopadłej, okręgi, dla innych elipsy

Slide 34

y b x2 a 2 1 Pomijając jedynkę otrzymamy: y bx a dwie proste na płaszczyźnie, stożek w przestrzeni Na płaszczyźnie (płaskim ekranie) otrzymamy krzywe stożkowe; dla płaszczyzny równoległej do prostej na której leżą źródła, hiperbole, dla płaszczyzny prostopadłej, okręgi, dla innych elipsy liczba hiperbol: mmax 2c

Slide 35

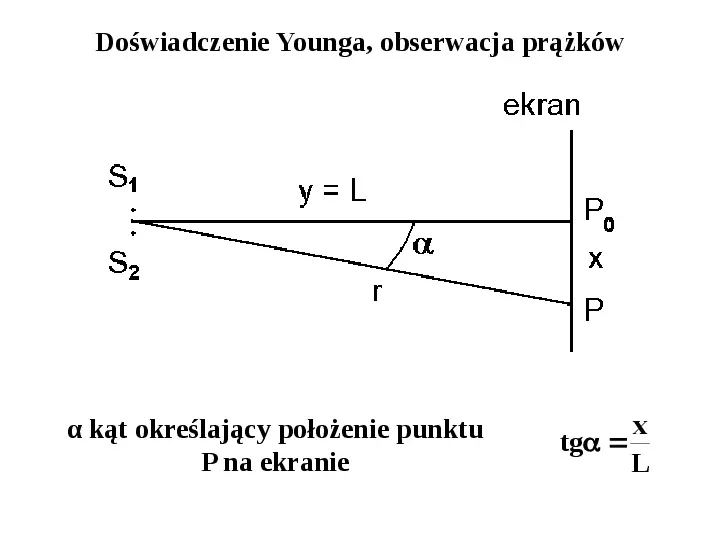
Doświadczenie Younga, obserwacja prążków α kąt określający położenie punktu P na ekranie x tg L

Slide 36

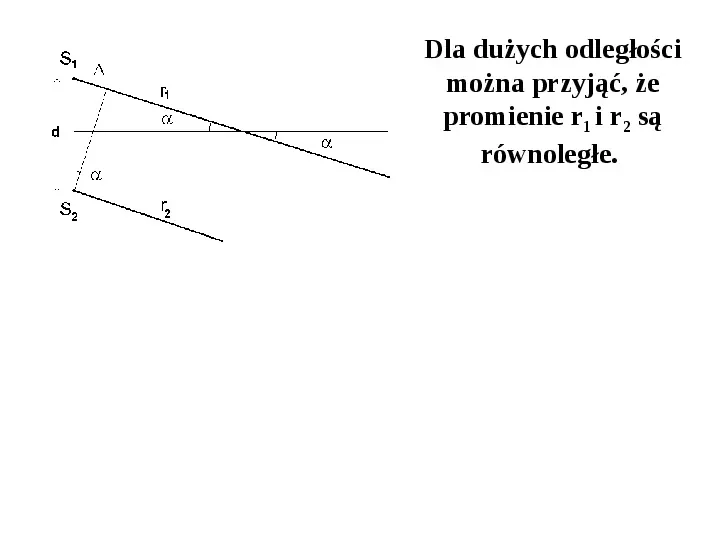
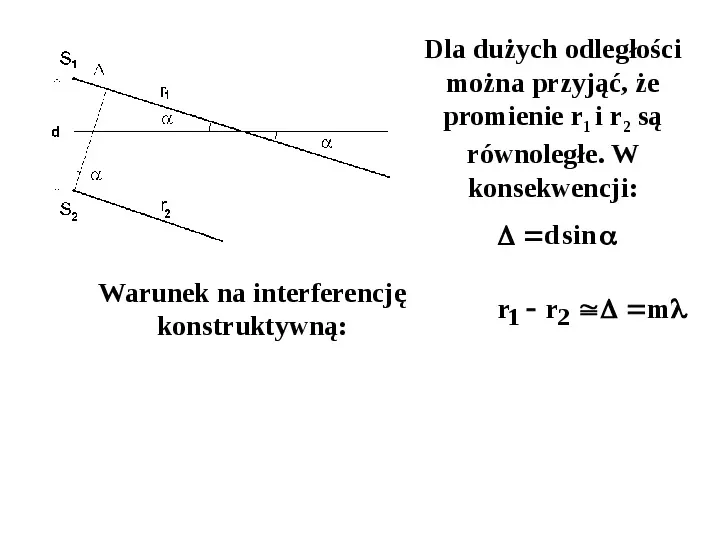
Dla dużych odległości można przyjąć, że promienie r1 i r2 są równoległe.

Slide 37

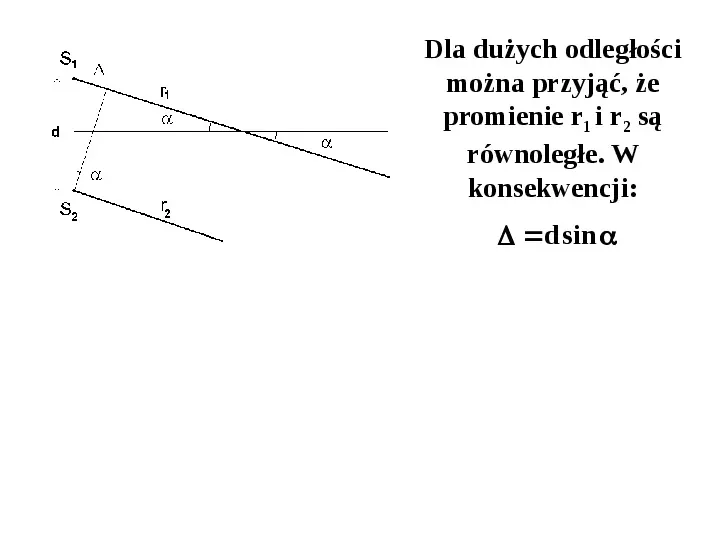
Dla dużych odległości można przyjąć, że promienie r1 i r2 są równoległe. W konsekwencji: d sin

Slide 38

Dla dużych odległości można przyjąć, że promienie r1 i r2 są równoległe. W konsekwencji: d sin Warunek na interferencję konstruktywną: r1 r2 m

Slide 39

Dla dużych odległości można przyjąć, że promienie r1 i r2 są równoległe. W konsekwencji: d sin Warunek na interferencję konstruktywną: x uwzględniając: tg , L da na położenie prążków jasnych: r1 r2 m dla małych kątów α xm m L d

Slide 40

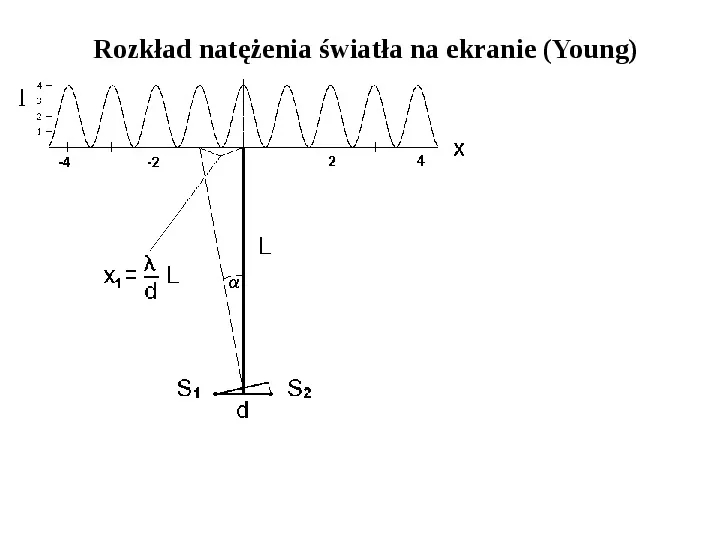
Rozkład natężenia światła na ekranie (Young)

Slide 41

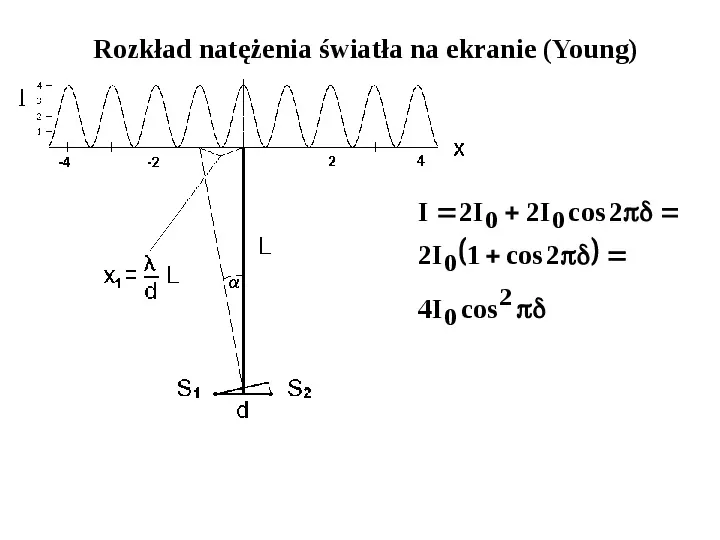
Rozkład natężenia światła na ekranie (Young) I 2I 0 2I 0 cos 2 2I 0 1 cos 2 4I 0 cos 2

Slide 42

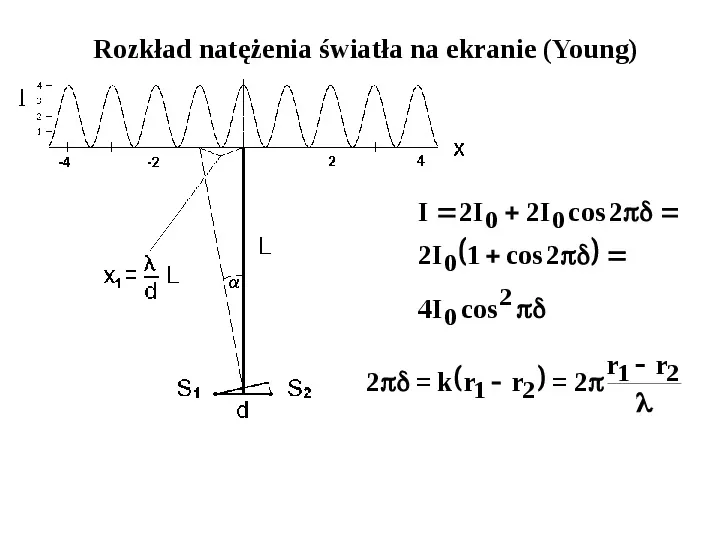
Rozkład natężenia światła na ekranie (Young) I 2I 0 2I 0 cos 2 2I 0 1 cos 2 4I 0 cos 2 r1 r2 2 k r1 r2 2

Slide 43

Rozkład natężenia światła na ekranie (Young) I 2I 0 2I 0 cos 2 2I 0 1 cos 2 4I 0 cos 2 r1 r2 2 k r1 r2 2 r1 r2 x L L d

Slide 44

Rozkład natężenia światła na ekranie (Young) I 2I 0 2I 0 cos 2 2I 0 1 cos 2 4I 0 cos 2 r1 r2 2 k r1 r2 2 r1 r2 x L L d d x, lub x L L d

Slide 45

PODSUMOWANIE zjawiska dyfrakcji i interferencji to odstępstwa od modelu promieni, spowodowane falową naturą światła (skończona długość fali) zjawisko interferencji to nakładanie się fal przechodzących przez kilka otworów zjawisko dyfrakcji to nakładanie się fal przechodzących przez różne fragmenty tego samego otworu

Slide 46

PODSUMOWANIE o znaczeniu efektów dyfrakcji interferencji i dyfrakcji decyduje długość fali λ, wymiary otworów (otworu) R i odległość ekranu obserwacyjnego L dla L R R efekty dyfrakcyjne i interferencyjne dominują Dyfrakcja (interferencja) FRAUNHOFERA dla L R R dyfrakcja i interferencja modyfikują obraz geometryczny Dyfrakcja (interferencja) FRESNELA

Slide 47

PODSUMOWANIE Występowanie interferencji i dyfrakcji zależy także od spójności czasowej (monochromatyczności) i przestrzennej światła. Brak spójności czasowej to brak korelacji pomiędzy falami wyemitowanymi w różnych chwilach czasu przez to samo źródło światła; brak spójności przestrzennej to brak korelacji pomiędzy fazami światła emitowanego przez różne fragmenty klasycznego źródła światła

Slide 48

PODSUMOWANIE W doświadczeniu Younga (dwa otwory lub szczeliny) obserwujemy strukturę dyfrakcyjną; w tym prążek główny o szerokości R L R oraz nałożoną, na ogół gęstszą strukturę jasnych i ciemnych prążków interferencyjnych. Dla prążków jasnych różnica dróg jest równa całkowitej wielokrotności długości fali. Odległość pomiędzy prążkami jasnymi (lub ciemnymi) wynosi: x L d