Zobacz slidy
Treść prezentacji
Slide 1
80 urodziny Kubusia Puchatka
Slide 2
14 października 1926 roku wydana została w Londynie książka pt.: Kubuś Puchatek. Od tego czasu aż po dzień dzisiejszy, dzieci na całym świecie zachwycają się przygodami zabawnego misia o bardzo małym rozumku
Slide 3
Krótka historia najbardziej znanego w świecie misia Twórcą Kubusia Puchatka jest Alan Alexander Milne Pisarz urodził się w 1882 r. w Londynie. Uczęszczał do Westminister School, a następnie do Trinity College w Cambridge, gdzie w 1903 roku ukończył matematykę. W październiku 1920 roku urodził się jego jedyny syn Christopher Robin (Krzyś). Od tego momentu Alan zaczął pisać liczne wiesze, które ofiarowywał swojej żonie jako prezenty. Ona zaś wysyłała je prosto do magazynów. Wkrótce stało się głośno o jego krótkich utworach, a sam Milne został poproszony o więcej W 1924 r. rozpoczyna się kariera A.A. Milnea jako twórcy książek dla dzieci.
Slide 4
Na pierwsze urodziny w 1921 roku Milne podarował swemu synowi pluszowego misia z luksusowego sklepu Harrodsa w Londynie. Krzyś prawie nigdy nie rozstawał się ze swoim misiem. Wspólne zabawy syna z ukochaną zabawką, stały się natchnieniem dla pisarza i tym sposobem Krzyś, jego miś oraz przyjaciele zwierzaki oglądane wspólnie w londyńskim ogrodzie zoologicznym stały się wkrótce literackimi postaciami.
Slide 5
W latach dwudziestych jednym z ulubieńców w londyńskim ogrodzie zoologicznym był niedźwiedź o imieniu Winnie. Syn autora Krzyś nazwał tym imieniem pluszowego misia, z którym się nie rozstawał od swoich pierwszych urodzin. Dlatego też pierwszy zbiór opowiadań, który ukazał się w październiku 1926 r. nosił tytuł Winnie the Pooh. Dwa lata później, w roku 1928 dzieci mogły już przeczytać dalsze przygody Kubusia w książce pt.: Chatka Puchatka. Jeszcze za życia Milnea, który zmarł 31 stycznia 1956 roku, przygody małego misia i jego przyjaciół zostały przetłumaczone na 12 języków i sprzedane w 7 milionach egzemplarzy.
Slide 6
Dorosły już Krzyś napisał książkę o sobie, zatytułowaną Poza światem Puchatka. Jak dowiadujemy się z jego wspomnień, w dzieciństwie chłopiec był niemal chorobliwie nieśmiały. Miał dziewczęcy wygląd, który nadawała mu matka, gdyż zawsze chciała mieć córkę. We swoich wspomnieniach opowiada również o tym, jak w czasie II wojny światowej walczył na froncie. W tej wojnie, po tej samej stronie co Anglicy, walczyli żołnierze z innych krajów, także z Polski. Musieli się uczyć języka angielskiego, by móc się wzajemnie porozumiewać. I wiecie, czym posługiwano się podczas tej nauki? Tekstami z książeczek o Kubusiu Puchatku. Żartowano później, że w ten sposób Puchatek przyczynił się do zwycięstwa Anglii i sprzymierzonych z nią państw w II wojnie światowej.
Slide 7
Pierwsze ilustracje z książki Kubuś Puchatek
Slide 8
Rysunki ilustrujące treść książki wzorowane były na zabawkach, którymi bawił się Krzyś.
Slide 9
Obecnie prawa autorskie do postaci stworzonych przez Alana Aleksandra Milne należą do koncernu Walta Disneya
Slide 10
Bajkowy świat Kubusia Puchatka
Slide 11
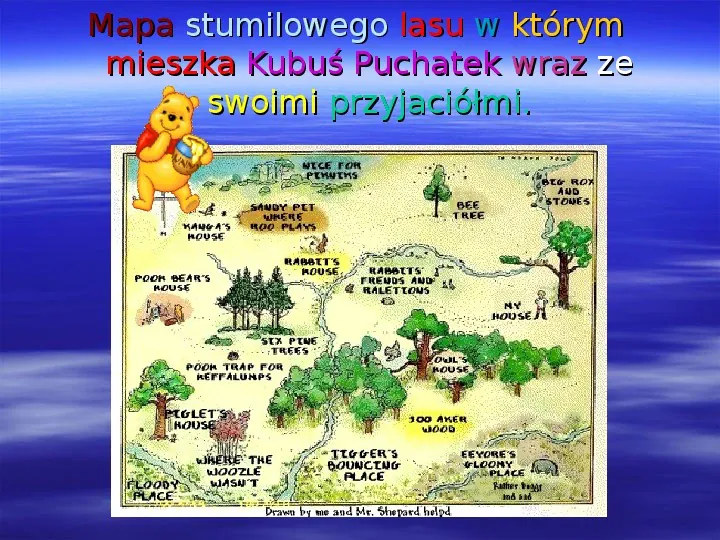
Mapa stumilowego lasu w którym mieszka Kubuś Puchatek wraz ze swoimi przyjaciółmi.
Slide 12
Parę słów o solenizancie i jego gościach Kubuś Puchatek nazywany jest przez przyjaciół i siebie samego Misiem o Bardzo Małym Rozumku, co doskonale go opisuje, gdyż pomysły misia są często łagodnie mówiąc nierozsądne. Mieszka w domku w drzewie. Uwielbia miód i potrafi cieszyć się wszystkim i jest wszystkim życzliwy. Jeżeli nawet nie potrafi pomóc, jest dumny z tego, że się starał. Stale przekręca wyrazy i wyśpiewuje swoje mruczanki.
Slide 13
Ulubiona mruczanka misia Dziwny jest niedźwiedzi ród, Że tak bardzo lubi miód, Bzyk-bzyk-bzyk, ram-pampam, Co to znaczy? Nie wiem sam!
Slide 14
Prosiaczek Najbliższy przyjaciel Puchatka. Prosiaczek jest bardzo niewielkiego wzrostu, co przyczyniło się do wykształcenia u niego cechy wyjątkowej bojaźliwości. Boi się właściwie wszystkiego, lecz najbardziej tego, co jest od niego większe, a rzeczy takich jest wiele. Kubuś lubi odwiedzać Prosiaczka, a Prosiaczek Kubusia.
Slide 15
Królik Królik to pewny siebie organizator, pracowity i wiecznie zabiegany. Trochę lekceważy swoich krewnych i znajomych. Charakterystyczne jest u niego to, iż najbardziej kocha marchewkę, którą hoduje w prywatnym ogródku warzywnym. Królik często się irytuje, a najbardziej wtedy gdy wbryknie na niego Tygrys, ale pomimo tego jest lubiany przez wszystkich mieszkańców Lasu.
Slide 16
Tygrysek Znany jest ze swej brykającej natury, wiecznie skory do zabawy. Pojawił się w Stumilowym Lesie później niż Kubuś czy Prosiaczek i od razu rozruszał panującą tam atmosferę. Uwielbia zaskakiwać, a często też straszyć mieszkańców Lasu, wskakując na nich i powalając na ziemię. W małym kangurku znalazł bardzo dobrego towarzysza zabaw. Lubi się przechwalać, że jest jedyny i niepowtarzalny.
Slide 17
Maleństwo Najmłodszy mieszkaniec Stumilowego Lasu, żyje razem z noszącą go w torbie nadopiekuńczą mamą Kangurzycą. Tak, jak jego dobry przyjaciel Tygrys, Maleństwo ma ogromne skłonności do brykania oraz absolutnie uwielbia swego prążkowanego kompana. Nie pragnie niczego innego, jak tylko zaimponować Tygrysowi i robić to, co Tygrys robi najlepiej.
Slide 18
Kangurzyca Jest wyrozumiałą i troskliwą matką małego Kangurzątka, które wychowuje samotnie. Ma też swoisty spryt i matczyną przenikliwość. Przyjęła pod swój dach Tygrysa, który stał się wspaniałym towarzyszem zabaw dla Maleństwa.
Slide 19
Kłapouchy Jest pluszowym osiołkiem z przyczepionym pinezką ogonem, zakończonym kokardą,. Ogon ma skłonność do częstego odpadania. Kłapouchy mieszka w Stumilowym lesie, w zbudowanym przez siebie szałasie z patyków, przypominającym stertę chrustu. O żadnym dniu nie mówi, że jest dobry, wyolbrzymia swoje niepowodzenia. Mimo tego lubią go wszyscy za jego marzycielską naturę. Pomagają Kłapouchemu znajdować ogon, który stale gdzieś gubi.
Slide 20
Sowa Przemądrzała Sowa Przemądrzała Jest najbardziej uczonym mieszkańcem Stumilowego. Inne stworzenia z Lasu często zwracają się do Sowy z problemami natury naukowej. Sowa ze swej strony twierdzi, iż umie bardzo dobrze czytać i pisać, co jednak jest dość dyskusyjne.
Slide 21
Ciekawostki Kubuś Puchatek ma własną gwiazdę w hollywoodzkiej Alei Sław. Miś o Bardzo Małym Rozumku dołączył do kilkunastu wyróżnionych w ten sposób animowanych postaci - wśród nich są takie gwiazdy jak Myszka Miki i Kaczor Donald. Na ekranach kin ukazał się nowy film o przygodach Kubusia Puchatka zatytułowany Kubuś Puchatek i Hefalumpy Wytwórnia Disneya przygotowuje również kolejny film, który trafi na ekrany w 2007 roku. Już dzisiaj wiadomo, że przyjacielem Misia o Bardzo Małym Rozumku nie będzie Krzyś, tylko rudowłosa, rozbrykana 6latka.
Slide 22
Dużo miodku, przygód wiele, wesołemu Puchatko wi życzą przyjaciel e!!!
Dane:
- Liczba slajdów: 22
- Rozmiar: 0.98 MB
- Ilość pobrań: 192
- Ilość wyświetleń: 8097