Zobacz slidy
Treść prezentacji
Slide 1
Układ Słoneczn Prezentacja multimedialna 2002 Tomasz Jarus
Slide 2
Układ heliocentryczny Mikołaj Kopernik Jan Matejko Astronom Kopernik albo rozmowa z Bogiem.
Slide 3
VOLUTIONIBUS ORBIUM COELE (O obrotach sfer niebieskich)
Slide 4
Powstanie Układu Sł
Slide 5
Dziewięć planet wchodzących
Slide 6
Układ Słoneczny Merkury Saturn Wenus Ziemia Mars Jowisz Uran Neptun Pluton
Slide 7
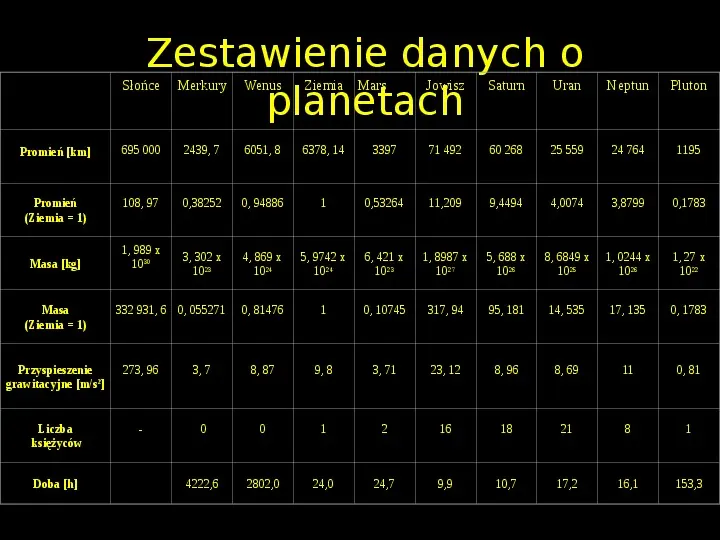
Zestawienie danych o planetach Słońce Merkury Wenus Ziemia Promień [km] 695 000 2439, 7 6051, 8 6378, 14 Promień (Ziemia 1) 108, 97 0,38252 0, 94886 3, 302 x 1023 Masa [kg] Masa (Ziemia 1) 1, 989 x 1030 332 931, 6 0, 055271 Mars Jowisz Saturn Uran Neptun Pluton 3397 71 492 60 268 25 559 24 764 1195 1 0,53264 11,209 9,4494 4,0074 3,8799 0,1783 4, 869 x 1024 5, 9742 x 1024 6, 421 x 1023 1, 8987 x 1027 5, 688 x 1026 8, 6849 x 1025 1, 0244 x 1026 1, 27 x 1022 0, 81476 1 0, 10745 317, 94 95, 181 14, 535 17, 135 0, 1783 Przyspieszenie grawitacyjne [ms2] 273, 96 3, 7 8, 87 9, 8 3, 71 23, 12 8, 96 8, 69 11 0, 81 Liczba księżyców - 0 0 1 2 16 18 21 8 1 4222,6 2802,0 24,0 24,7 9,9 10,7 17,2 16,1 153,3 Doba [h]
Slide 8
Planetoidy
Slide 9
Komety
Slide 10
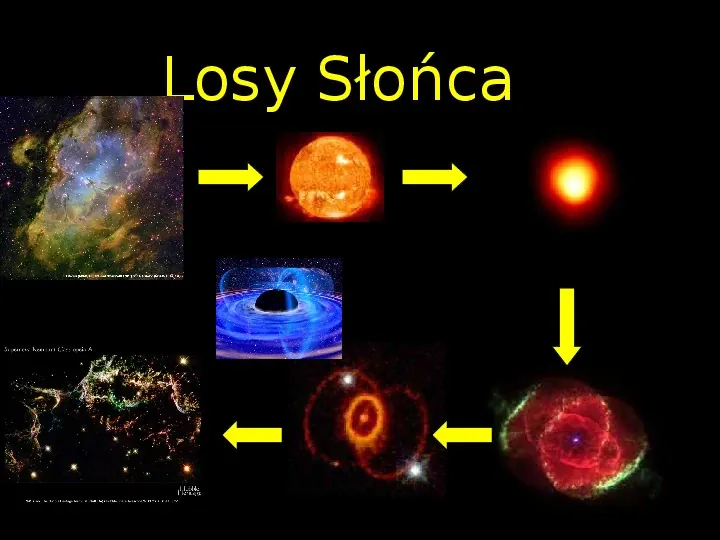
Losy Słońca
Slide 11
Dziękuję za uwagę
Dane:
- Liczba slajdów: 11
- Rozmiar: 3.73 MB
- Ilość pobrań: 13669
- Ilość wyświetleń: 60454