Sport to zdrowie

Zobacz slidy

Treść prezentacji

Slide 1

Sport to zdrowie.

Slide 2

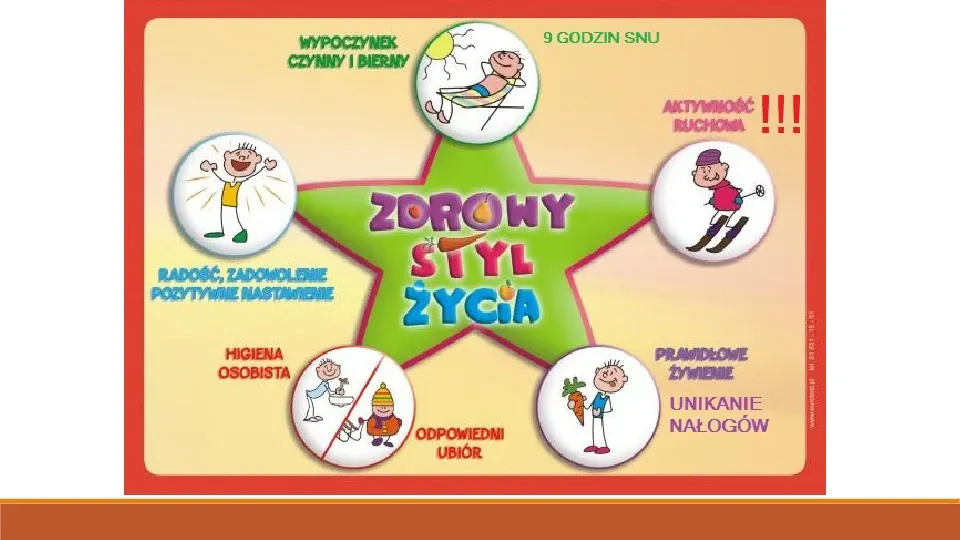
Zdrowy styl życia Sposób postępowania, który sprzyja zachowaniu zdrowia i zapewnia dobre samopoczucie, nazywa się zdrowym stylem życia.

Slide 4

Aby zachować zdrowie nie wystarczy prawidłowo się odżywiać, należy też koniecznie pamiętać o aktywności fizycznej na co dzień! Aktywność fizyczna jest bardzo ważna, zarówno w życiu młodych osób, jak i starszych. Warto pamiętać, że uprawianie sportu nie tylko wpływa na ładną sylwetkę i dobrą wydolność organizmu, ale również zapobiega wielu chorobom. Dlatego w każdym wieku należy się ruszać w miarę swoich możliwości.

Slide 5

Co daje nam aktywność fizyczna? Aktywność fizyczna pozwala nam: poprawić lub zachować wydolność fizyczną, utrzymać odpowiednią wagę, zachować siłę mięśniową, która stabilizuje stawy i kręgosłup, na wzrost odporności, zapobiegać chorobom cywilizacyjnym, w tym chorobom serca,

Slide 6

Co daje nam aktywność fizyczna? ciąg dalszy osiągnąć lepsze samopoczucie Pod wpływem wysiłku fizycznego w naszym organizmie wytwarzają się endorfiny tzw. hormon szczęścia. Pod ich wpływem poprawia się nam samopoczucie, pojawia się uczucie odprężenia, szczęścia. Podczas wysiłku fizycznego następuje przypływ dobrych uczuć i pozytywnych emocji. zmniejszyć napięcie i stres, osiągać większą sprawność umysłu Nasz mózg pracuje sprawniej, jeżeli regularnie wykonujemy wysiłek fizyczny.

Slide 7

Wpływ ruchu na nasze zdrowie Wysiłek fizyczny powoduje: lepsze ukrwienie najważniejszych narządów takich jak serce i mózg, obniżenie poziomu cukru we krwi, obniżenie poziomu złego cholesterolu, podwyższenie dobrego cholesterolu, obniżenie poziomu trójglicerydów.

Slide 8

Formy aktywności fizycznej BIEGANIE Regularnie uprawiany jogging ma wiele zalet. Po pierwsze, faktycznie wpływa na wzmocnienie odporności oraz wytrzymałości organizmu, dzięki czemu stajemy się silniejsi i bardziej zahartowani. Po drugie, bieganie przeciwdziała poważnym chorobom oraz dolegliwościom takim jak zawały serca, depresja, nerwica, cukrzyca. Po trzecie, podczas tej aktywności fizycznej wydzielają się hormony szczęścia, czyli endorfiny. To sprawia, że bieganie jest nie tylko dobre dla zdrowia, ale także sprawia prawdziwą przyjemność. JAZDA NA ROWERZE Regularne korzystanie z roweru pomaga pozbyć się niechcianych kilogramów, skutecznie rozprawia się z cellulitem oraz poprawia krążenie krwi w żyłach, czyli zapobiega żylakom. Co więcej, to doskonały sposób na redukcję stresu. Jazda na rowerze wzmacnia również serce, obniża poziom złego cholesterolu oraz pozytywnie wpływa na kręgosłup.

Slide 9

Formy aktywności fizycznej ciąg dalszy PŁYWANIE Pływanie wpływa przede wszystkim na poprawę metabolizmu, wysmuklenie sylwetki oraz wzmocnienie odporności. Kiedy pływamy, zaczynają pracować wszystkie nasze grupy mięśniowe, więc to jeden z najbardziej rozwojowych oraz efektywnych treningów. Dodatkowo, sport ten zwiększa pojemność płuc, pozytywnie wpływa na ukrwienie skóry, pomaga zwalczyć cellulit oraz doskonale relaksuje, dlatego polecany jest osobom zmagającym się z przewlekłym stresem.  NORDIC WALKING Trening nordic walking pozytywnie wpływa na rozwój kondycji oraz odporności organizmu. Dodatkowo, dzięki kijkom i przy odpowiedniej technice ich używania odciążamy stawy. I INNE, M.IN. SPACERY, SIATKÓWKA, PIŁKA NOŻNA, TENIS ZIEMNY, JAZDA NA ROLKACH (ZIMĄ NA ŁYŻWACH) ITP.

Slide 10

PIRAMIDA AKTYWNOŚCI FIZYCZNEJ

Slide 11

Wydatek energetyczny w kcalh bieg szybki - 1120 boks - 868 czołganie się - 800 gimnastyka lekka - 170 jazda na łyżwach - 718 jazda na nartach - 600 jazda na rowerze (10kmh) jazda na rowerze (20kmh) bieg szybki - 1120 boks - 868 czołganie się - 800 gimnastyka lekka - 170 jazda na łyżwach - 718 jazda na nartach - 600 jazda na rowerze (10kmh) jazda na rowerze (20kmh) - 270 - 650 - 270 - 650

Slide 12

Zagrożenia wynikające z braku aktywności ruchowej nadciśnienie tętnicze, choroby serca, otyłość, osteoporoza, udar mózgu, depresja, rak jelita grubego.

Slide 13

Literatura: podręcznik do klasy czwartej szkoły podstawowej Tajemnice przyrody, Maria Marko-Worłowska, Nowa Era, Warszawa 2012 https:portal.abczdrowie.plwplyw-aktywnosci-fizycznej-na-zdrowie http:ecoblik.plfeaturedrozne-formy-aktywnosci-fizycznej-i-ich-wplyw-nazdrowie http:www.zachowajrownowage.plplpiramida-aktywnosci-fizycznej-dladzieci-w-wieku-przedszkolnym-i-wczesnoszkolnym-2

Slide 14

SPORT TO ZDROWIE, UŚWIADOM TO SOBIE!