Prawa rozpadu promieniotwórczego

Zobacz slidy

Treść prezentacji

Slide 1

Prawa rozpadu promieniotwórczego Prawa rozpadu promieniotwórczego podlegają rozkładowi statystycznemu. Nie można przewidzieć kiedy dany atom ulegnie rozpadowi. W jądrze zachodzą ciągłe zmiany rozkładu energii i w każdej chwili może zdarzyć się konfiguracja implikująca zaistnienie rozpadu promieniotwórczego. Jeżeli odpowiednio duża liczba rozpadów promieniotwórczych jest obserwowana można zaobserwować prawo rozpadu. Aktywność (A) radionuklidu jest jego szybkością rozpadu promieniotwórczego - dN wyrażana równaniem: dt dN A N dt gdzie: jest współczynnikiem proporcjonalności zwanym stałą rozpadu, dN oznacza liczbę atomów, które uległy rozpadowi w czasie dt, znak minus oznacza promieniotwórczego. zmniejszenie się liczby atomów wskutek rozpadu

Slide 2

Liczba atomów pierwiastka promieniotwórczego, rozpadających się w jednostce czasu, jest w każdej chwili proporcjonalna do ogólnej liczby atomów tego pierwiastka. Rozdzielając zmienne i całkując (w granicach No, N) otrzymujemy: N dN N tdt No ln N t No lub w postaci wykładniczej N N o e t gdzie: N liczba atomów po czasie t, No początkowa liczba atomów, - stała rozpadu, t czas.

Slide 3

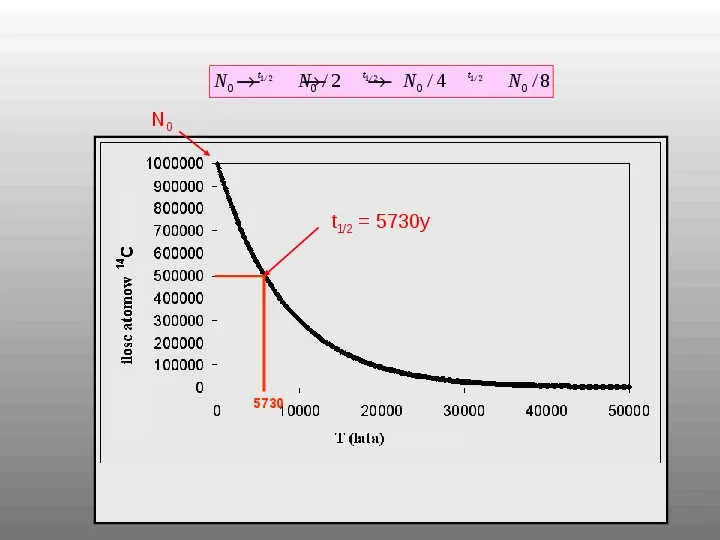
Okres, po którym liczba atomów pierwiastka zmniejszyła się o połowę nosi nazwę czasu połowicznego rozpadu. N N oe t No N 2 No N o e t1 2 2 1 ln( ) t1 2 2 t1 2 ln 2 0,693

Slide 4

N0 t1 2 N 0 2 N0 4 t1 2 N0 t12 5730y 5730 t1 2 N0 8

Slide 5

Jednostką radioaktywności jest w systemie SI bequerel (Bq) 1Bq 1 rozpads Starszą jednostką jednak wciąż stosowaną jest curie (Ci) 1Ci aktywność (ilość rozpadóws) 1 g 226Ra Czas połowicznego rozpadu 226Ra t12 1600 lat 5,05x1010 s A λN Ra N Av ln 2 6,03x10 23 x0,693 1Ci x 3,7 x1010 Bq 10 M at t1 2 226 x5,05 x10 Aktywność właściwa Aw A (Bqg) m

Slide 6

Równowaga promieniotwórcza nuklid 1 nuklid 2 onuklid 3 np.: 90 Sr 90Y 90Zr nuklid 1 jest nuklidem macierzystym (mother) nuklid 2 jest pochodnym (daughter) nuklid 3 (granddaughter) Szybkość produkcji (narastania) nuklidu 2 ( ) czyli rozpadu N1 jest proporcjonalna dN 2 dt do ilosci atomow N1 i jest równa różnicy szybkości rozpadu nuklidu 1 i rozpadu nuklidu 2 dN 2 1N1-2N2 dt

Slide 7

Rozwiązując równanie różniczkowe dochodzimy do równania 1 N2 N1[1 e (2 1)t ] 2 1 Można wyróżnić następujące przypadki: t12(1) t12(2) czyli 1 2 wzór upraszcza się do 1 N 2 N 1 (1 e 2t ) 2 po około 10 x t12 e 2t 0 i N 2 1 t1 2 (2) N1 2 t1 2 (1)

Slide 8

N 2 1 t1 2 (2) N1 2 t1 2 (1) Jest ważny i częsty przypadek w pomiarach radiochemicznych np. pomiar 137 30lat 137 Cs 2,55min Cs 137m Ba 137 Ba aby zmierzyć aktywność 137Cs po wydzieleniu jego z próbki należy odczekać ok. 25 min aż powstanie równowagowa ilość atomów 137mBa. Wzór też pozwala na obliczenie czasu połowicznego rozpadu długożyjących izotopów np. 226 1600lat Ra 222 3dni Rn Znając aktywność i t12 222Rn możemy obliczyć ilość atomów 222Rn. Znając masę preparatu 226 Ra możemy obliczyć jego ilość jego atomów, a ze wzoru czas życia.

Slide 9

t12(1) t12(2) czyli 1 2 Izotop pochodny ma znacznie dłuższy czas życia niż macierzysty Nuklid macierzysty zanika i narasta nuklid pochodny. Nie ustala się równowaga promieniotwórcza. 99 m Np. 6 godz. 99 2,1x105 lat Tc Tc 99 Ru t12(1) t12(2) czyli 1 2 Przy bardzo zbliżonych czasach rozpadu równowaga silnie zależy, który izotop rozpada się wolniej

Slide 10

Sukcesywna przemiana promieniotwórcza 1234.. n..... Równanie dN n n-1Nn-1-nNn dt Rozwiażanie tego równania jest złożone, ale bardzo szybkie numerycznie. Z rozwiązania tego równania dochodzimy do fundamentalnej zależnośći że w jakimkolwiek szeregu promieniotwórczym niezależnie od czasu życia poszczególnych nuklidów w stanie równowagi promieniotwórczej aktywności nuklidów są takie same: A(1)A(2)A(3).... Ilość atomów (moli) pierwiastków promieniotrczych w szeregu promieniotworczym w stanie rownowagi: N1 T1 2 (1) N n T1 2 (n)

Slide 11

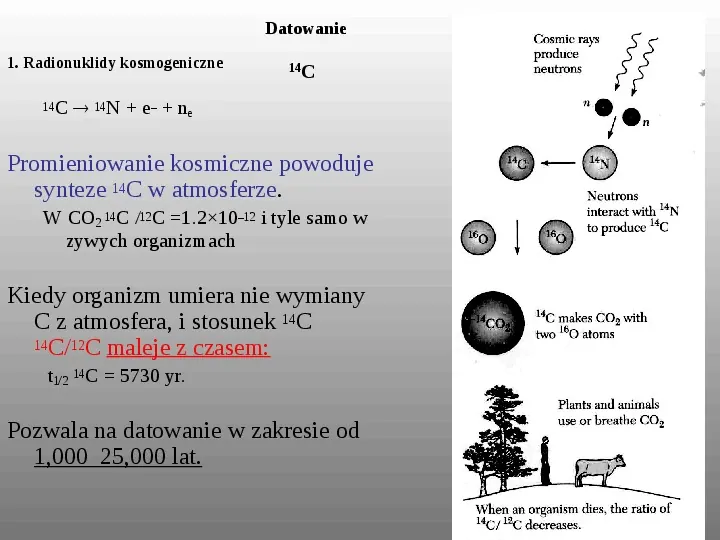
Datowanie 1. Radionuklidy kosmogeniczne 14 14 C C 14N e ne Promieniowanie kosmiczne powoduje synteze 14C w atmosferze. W CO2 14C 12C 1.21012 i tyle samo w zywych organizmach Kiedy organizm umiera nie wymiany C z atmosfera, i stosunek 14C 14C12C maleje z czasem: t12 14C 5730 yr. Pozwala na datowanie w zakresie od 1,000 25,000 lat.

Slide 12

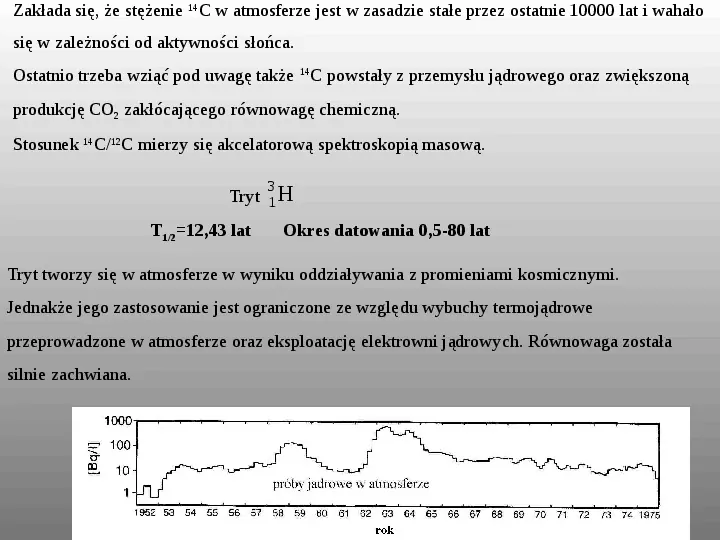
Zakłada się, że stężenie 14C w atmosferze jest w zasadzie stałe przez ostatnie 10000 lat i wahało się w zależności od aktywności słońca. Ostatnio trzeba wziąć pod uwagę także 14C powstały z przemysłu jądrowego oraz zwiększoną produkcję CO2 zakłócającego równowagę chemiczną. Stosunek 14C12C mierzy się akcelatorową spektroskopią masową. 3 Tryt 1 H T1212,43 lat Okres datowania 0,5-80 lat Tryt tworzy się w atmosferze w wyniku oddziaływania z promieniami kosmicznymi. Jednakże jego zastosowanie jest ograniczone ze względu wybuchy termojądrowe przeprowadzone w atmosferze oraz eksploatację elektrowni jądrowych. Równowaga została silnie zachwiana.

Slide 13

W butelce starego wina na którego etykiecie była data produkcji 1937 r. zmierzono stężenie T2O (T tryt) i porównano go ze stężeniem T2O w wodzie powierzchniowej. Stężenie T w winie było 4 razy mniejsze niż w wodzie. Czy data produkcji na butelce była prawdziwa? Stężenie trytu w winie stanowiło 25 stężenia w wodzie Po 12,4 lat stężenie T wynosi 50 Po 24,8 lat - - wynosi 25 Czyli wino miało około 25 lat. Przykład 2 Znaleziono drewniane szczątki prehistorycznej budowli. Pobrano próbkę, zwęglono ją zmierzono ilość 14C. Stwierdzono, że stosunek 14C12C w próbce był 2 razy niższy niż w CO2 w atmosferze. Z jakiego wieku pochodziła budowla?

Slide 14

Datowania geologiczne 238 92 U 206 82 Pb 207 235 Pb 92 U 82 Th 208 82 Pb 232 90 T124,5x109 lat Okres datowania3x107 lat T127x108 lat Okres datowania 5x106 lat T121,4x1010 lat Okres datowania 3x108 lat W datowaniu skał wykorzystuje się stosunek powstałych z rozpadu izotopów ołowiu 206 82 Pb 207 82 Pb 40 40 19 K 18 Ar 87 87 37 Rb 38 Sr 208 82 Pb do powstałego nie z rozpadu 204 82 Pb T124,8x1010 lat Okres datowania 5x108 lat T121,3x109 lat Okres datowania 3x107 lat

Slide 15

Można obliczyć wiek skorupy ziemskiej na podstawie składu izotopowego minerału uranitu 61,14 U, 18,1 Pb). Ponieważ masa atomowa ołowiu w uranicie wynosiła 206,06 jest więc równa masie atomowej 206 Pb. Można więc przyjąć, że cały ołów pochodził z rozpadu uranu. Stała rozpadu 238U 1,62x10-10 lat. 61,14 0,25689 238 18,1 0,087864 Liczba moli ołowiu w 100 g 206 Liczba moli uranu w 100 g Liczba atomów 238U w czasie pomiaru N 0,25689xNA , Początkowa liczba atomów 238U równa jest liczbie atomów 238U w czasie pomiaru ilość atomów powstałego z rozpadu 206 Pb No(0,256890,087864)xNA Z wzoru na rozpad N e t N0 1 N 2,303 0,25689N A t ln log 1,82 x109 lat N o 1,62 x10 10 034474N A

Slide 16

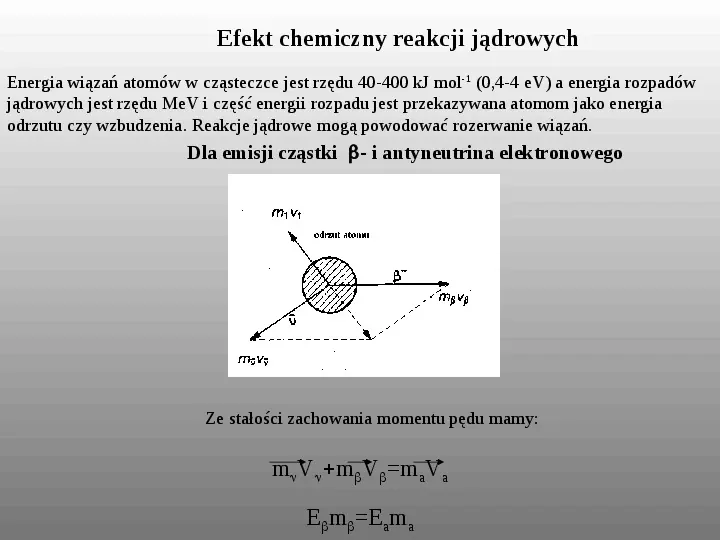
Efekt chemiczny reakcji jądrowych Energia wiązań atomów w cząsteczce jest rzędu 40-400 kJ mol -1 (0,4-4 eV) a energia rozpadów jądrowych jest rzędu MeV i część energii rozpadu jest przekazywana atomom jako energia odrzutu czy wzbudzenia. Reakcje jądrowe mogą powodować rozerwanie wiązań. Dla emisji cząstki- i antyneutrina elektronowego Ze stałości zachowania momentu pędu mamy: mVmVmaVa EmEama

Slide 17

Gdy cząstka ma prędkość zbliżoną do prędkości światła otrzymujemy po uwzględnieniu poprawki relatywistycznej: m o2 E 22 E1 E2 m1 2m1c 2 Emisja kwantu : E1 E2 2mc 2

Slide 18

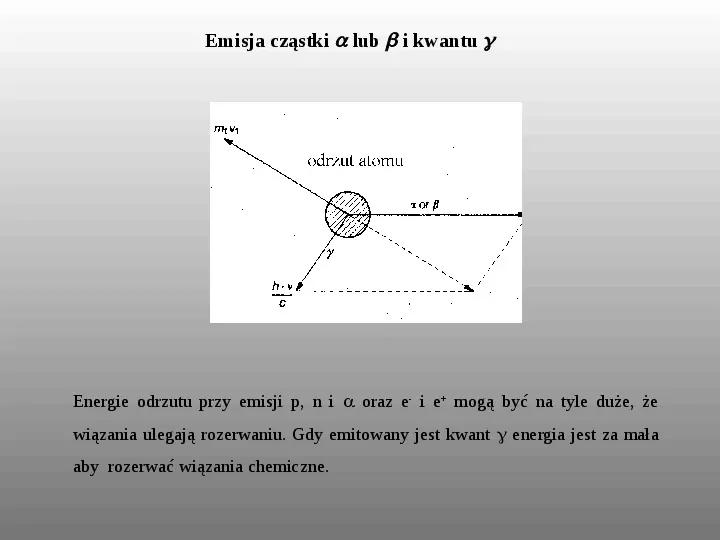
Emisja cząstki lub i kwantu Energie odrzutu przy emisji p, n i oraz e- i e mogą być na tyle duże, że wiązania ulegają rozerwaniu. Gdy emitowany jest kwant energia jest za mała aby rozerwać wiązania chemiczne.

Slide 19

Efekty wzbudzenia Reakcja jądrowa może wzbudzić powłoki elektronowe atomu poprzez: - energię odrzutu - zmianę liczby atomowej wskutek rozpadu - wychwyt elektronu lub przemianę wewnętrzną jądra Gdy energia odrzutu jest duża, część elektronów nie podąża za jądrem i następuje jonizacja. Atomy odrzutu po zerwaniu wiązań z cząsteczką poruszają się z dużą prędkością w ośrodku zawierającym atomy i cząsteczki. Atomy odrzutu przenikają powłoki elektronowe ulegają spowolnieniu wskutek jonizacji i wzbudzenia atomów środowiska. Mogą zachodzić reakcje nieosiągalne w innych warunkach.

Slide 20

W przemianie powstaje jądro ZZ-2, mamy dwa nadmiarowe elektrony, które mogą, być emitowane. Rn Po 2 - W skutek zmniejszania się ładunku jądra następuje ekspansja elektronów położonych blisko jądra. W przemianie efekty związane ze wzbudzeniem są znacznie mniejsze niż efekty odrzutu jądra. W skutek zmniejszania się ładunku jądra następuje ekspansja elektronów położonych blisko jądra. W przemianie efekty związane ze wzbudzeniem są znacznie mniejsze niż efekty odrzutu jądra. W przemianie rozpad cząsteczki w wyniku odrzutu jest możliwy jedynie w przypadku bardzo lekkich atomów i wysokiej energii cząstek . W innych przypadkach energia odrzutu wynosi ułamki eV co nie wystarcza do rozerwania wiązań.

Slide 21

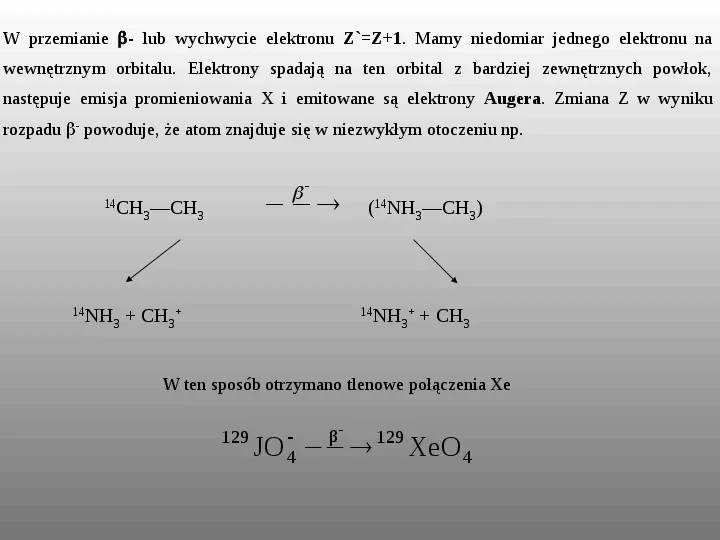
W przemianie - lub wychwycie elektronu ZZ1. Mamy niedomiar jednego elektronu na wewnętrznym orbitalu. Elektrony spadają na ten orbital z bardziej zewnętrznych powłok, następuje emisja promieniowania X i emitowane są elektrony Augera. Zmiana Z w wyniku rozpadu powoduje, że atom znajduje się w niezwykłym otoczeniu np. 14 14 CH3CH3 NH3 CH3 (14NH3CH3) 14 NH3 CH3 W ten sposób otrzymano tlenowe połączenia Xe 129 JO 4 β 129 XeO 4

Slide 22

Efekt Szilarda-Chalmersa Reakcje atomów gorących pozwalają otrzymać beznośnikowe izotopy. Po naświetleniu neutronami izotop w wyniku reakcji odrzutu lub wzbudzenia atomu znajduje się w innej formie niż nuklid macierzysty i może być wydzielony metodami chemicznymi. Np.: 127 3 JO (n, γ) 128 J

Slide 23

Wpływ wiązania chemicznego na rozpad jąder Wpływ otoczenia elektronowego najłatwiej zauważyć w przypadku wychwytu elektronowego lekkich atomów. Dla 7Be. 7 Be e 7 Li Be2- 1s2. Gęstość elektronów 1s w jądrze zmienia się w zależności od otoczenia. Zmiana t12t12x103 dla różnych związków 7Be w porównaniu z 7Be metalicznym związek t12t12x103 BeS 5,3 Be(H2O)42 2,3 Be(metal) 0 BeO -1,4 BeF2 -12,0 BeBr2 -16,2

Slide 24

Bardzo duży efekt obserwowano dla konwersji wewnętrznej 235mU (t1226,1 min). Poziom wzbudzenia jądra 235mU jest jedynie o 68 eV wyższy niż pozom podstawowy. Mogą więc ulegać konwersji jedynie elektrony o małej energii wiązania - z orbitali 6s, 7s, 6p, 5f i 6d. Energia tych elektronów będących walencyjnymi silnie zależy od otoczenia chemicznego Związek UC 26,2 UO2 24,7 235m 235m t12 (min.)

Slide 25

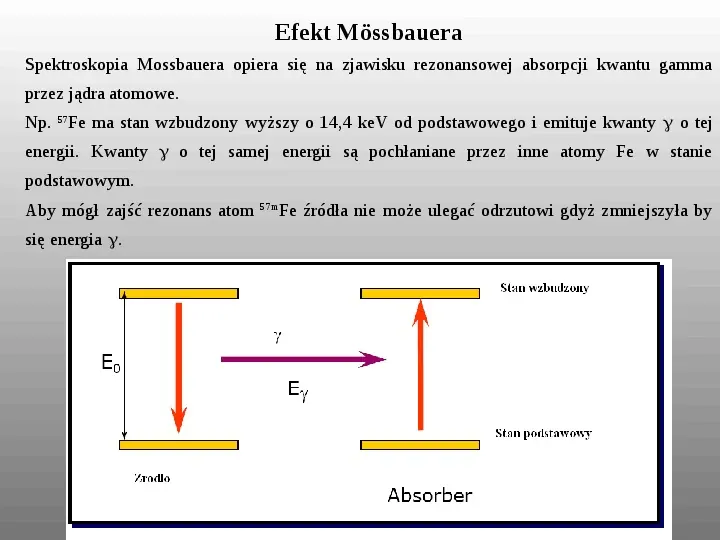
Efekt Mössbauera Spektroskopia Mossbauera opiera się na zjawisku rezonansowej absorpcji kwantu gamma przez jądra atomowe. Np. 57Fe ma stan wzbudzony wyższy o 14,4 keV od podstawowego i emituje kwanty o tej energii. Kwanty o tej samej energii są pochłaniane przez inne atomy Fe w stanie podstawowym. Aby mógł zajść rezonans atom się energia . Fe źródła nie może ulegać odrzutowi gdyż zmniejszyła by 57m

Slide 27

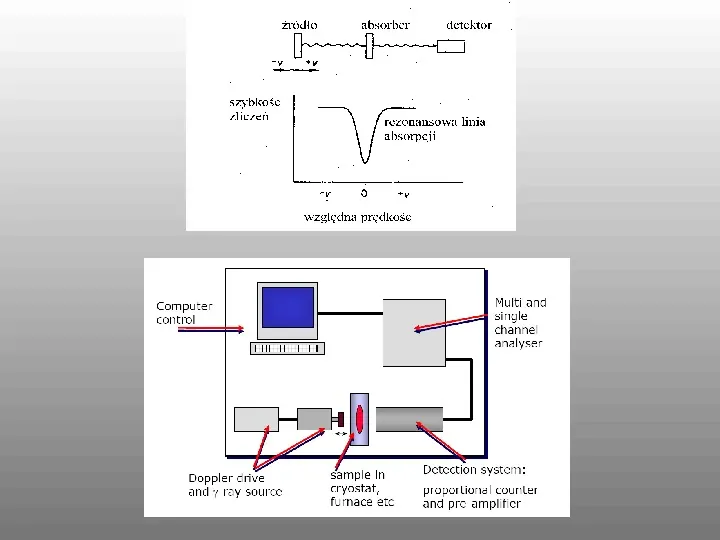
W krystalicznym ciele stałym atom Fe jest związany i nie ulega odrzutowi. Otoczenie elektronowe jądra może wpływać na poziom rezonansowy. Jeżeli otoczenie chemiczne atomu źródła i adsorbera jest różne nie może zajść rezonans. Ponieważ wpływ otoczenia elektronowego na poziomy rezonansowe jądra jest bardzo mały, do zajścia rezonansu wystarczy powoli przesuwać źródło względem adsorbera aby dodać energię kinetyczną fotonu (E). Szybkość przesuwu źródła jest tzw przesunięciem izomerowym - . Wielkość d zależy od otocznia elektronowego stopnia utlenienia, ligandowów etc. Nuklidy mogące być źródłami w spektroskopii Mossbauera muszą mieć czasy życia stanu wzbudzonego rzędu nanosekund. Energia fotonu nie może przekraczać 100eV. Najpopularniejszym żródłem jest 57Co rozpadający się do 57mFe (t1298ns). Adsorberem jest naturalne żelazo o zawartości 2,17 57Fe.

Slide 28

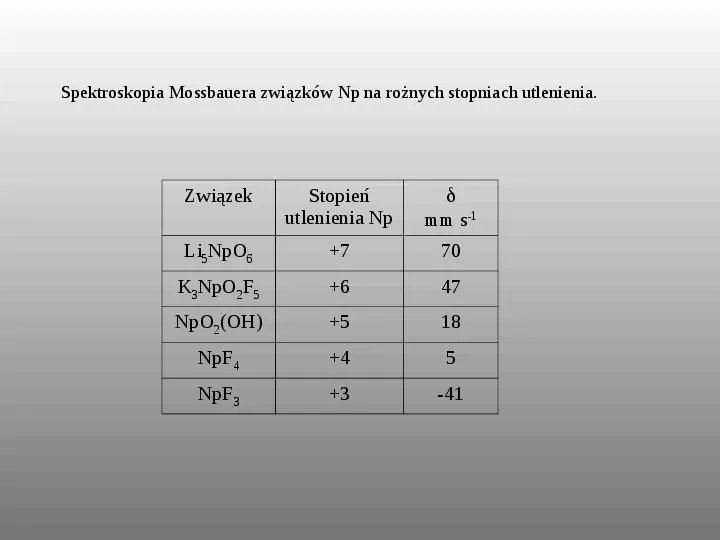
Spektroskopia Mossbauera związków Np na rożnych stopniach utlenienia. Związek Stopień utlenienia Np mm s-1 Li5NpO6 7 70 K3NpO2F5 6 47 NpO2(OH) 5 18 NpF4 4 5 NpF3 3 -41

Slide 29

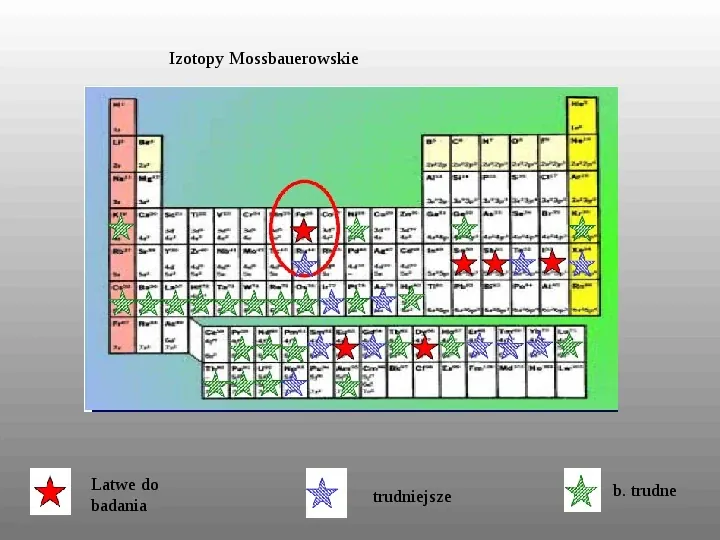
Izotopy Mossbauerowskie Latwe do badania trudniejsze b. trudne